Для реализации этой схемы можно выбрать значение емкости Ci (предпочтительно близкое к значению 10/fo мкФ, где /o=£oo/2jt) и из (7.4), (7.5) н (7.7) вычислить сопротивления. В результате получаем

;?2=2/ficu„C,;

R, = R, {[-К)Щ;

Rs = Ri/K;

Ri = Ri/(l-K).

(7.12)

Для частного случая, а именно К~1/2, эти выражения преобразуются к виду

R. = /?2/4; [

(7.13)

а уравнения (7.9) и (7.10) ся следующим образом; для 0<фо<180°

перепнсывают-

2tg(b/2) для - 180<у(,<0

l /l + 4tg (у„/2)

2tg(v.o/2)

(7.14)

(7.15)

В качестве примера предположим, что необходимо реализовать всепропускающий фильтр, который обеспечивает фазовый сдвиг фо=-90° на частоте fo=1000 Гц при коэффициенте усиления К=1/2. Из (7.15) получаем

а= (-1 - 15)/( - 2) = 1,618.

Выбирая Ci=10/l000=0,0I мкФ, из (7.13) находим

/?2=19,673 кОм; /?1=4,918 кОм;

3=i/?4=39,346 кОм.

Краткое описание всепропускающей схемы с МОС и методика ее расчета приведены в § 7.6.

7.3. БИКВАДРАТНЫЕ ВСЕПРОПУСКАЮЩИЕ ФИЛЬТРЫ

Коэффициенты усиления всепропускающей схемы, описанной в предыдущем параграфе, ограничены значениями, меньшими 1. Относительно простая в настройке биквадратная всепропускающая схема [8], с помощью которой можно достичь произвольного значения коэффициента усиления и добротности QlOO, показана на рис. 7.3. Уравнение (7.1) реализуется этой схемой при

6со2

,RbC\ (

(7.16)

и инвертирующем коэффициенте усиления

KRs/Ri

(7.17)

Рис. 7.3. Схема биквадратного всепропус-кающего фильтра.

и условии, что

RiRi2RiRs.

(7.18)

При выбранном значении Ci уравнениям (7.16)-(7.18) удовлетворяют следующие значения сопротивлений:

/?2= l/acOcC,; R, = R/2K; Rs=l/bw\C\R,i RRJK,

(7.19).

где Ri имеет произвольное значение.

При заданном значении фо==ф(юо) параметры а V. Ь связаны соотношением-(7.3). Таким образом, один из них можно выбирать произвольно. Если выбрать

(7.20)

то значение а определяется из (7.14) или (7.15). В этом случае при выборе /?5=?2. можно добиться значительного упрощения вычисления значений сопротивлений. Их результирующие значения

/?2= 1/оы„С,;

R = R/2K;

Rs - Rb = Ri.\ R = RJK.

(7.21),

Биквадратную схему можно настроить следующим образом: изменяя сопротивления Ri и Rs, установить соответственно параметры а и 6, которые при настройке задают значение фо, а затем, изменяя сопротивление Ri, установить коэффициент усиления.

Методика расчета приведена в § 7.7.

7.4. ФИЛЬТРЫ БЕССЕЛЯ

Если изображенная на рис. 7.1 фазо-частотная характеристика представляет собой прямую линию и определяется соотношением

ф(ш)=-йп. (7.22)

где т - постоянное число, то из уравнения 41-5) находим время замедления

(7.23)

Таким образом, линейная фазо-частот-таая характеристика (прямая линия) характеризуется постоянным временем замедле-<ния, что важно для многих применений «фильтров. Фильтр, для которого время замедления практически постоянно (в пределах некоторого заданного диапазона частот ОооЮс), является, следовательно, «фильтром с линейной фазой или постоянным временем замедления.

Наилучшим из полиномиальных филь--тров с постоянным временем замедления является фильтр Бесселя [27], нередаточ-«ая функция которого имеет вид:

(7.24)

(где К - коэффициент усиления фильтра, а Bn(s)-полином п-й степени

Bn(s)=S + 6n-lS-+ ...

... +6,5-1-60, (7.25)

йтде для й=0, 1, 2.....п,

= k\ (n-й)! [-2} (7-26)

Полином Bn{s) при (йс=1 относится .ж полиномам Бесселя, от которых и произошло название .фильтра.

Характеристика времени замедления -фильтра Бесселя максимально плоская, подобно амплитудно-частотной характеристи-ке фильтра Баттерворта. Это было пока-4ано Томсоном (Thomson) [30], он первым разработал их теорию, но не связал шолученные результаты с полиномами Бес-селя, поэтому существует другое название фильтров этого типа, а именно фильтр Томсона.

Для иллюстрации линейности фазо-частотной характеристики Бесселя на рис. 7.4 изображен ряд примеров. Их можно сравнить с приведенными ранее на рис. 2.9 фа-зо-частотными характеристиками фильтров Баттерворта и Чебышева. Очевидно, что характеристики фильтров Бесселя намного лучше. Однако амплитудно-частотная характеристика фильтра Бесселя хуже характеристик фильтров Баттерворта или Чебышева.

Для дальнейшего описания свойств .линейности фазы и постоянства времени замедления фильтра Бесселя можно показать, что для

0<а)<(йс (7.27)

время замедления моиотонио спадает от «го значения на частоте а)=0, равного

С ft5 1,0 1,5 2,0 О), рад/с с-h-1-1--1-1-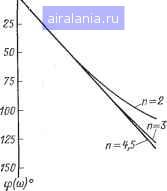

Рис. 7.4. Фазо-частотные характеристики фильтра Бесселя.

до значения на частоте to=a)c, которое составляет для п=2

12 0,92308 К) = ТЗ = -3, <7.29)

для п = 3

т, 0,99639 (-)=-277о=-- (7.30)

и для п-А

12745 0,99992

12746tOc tOc

(7.31)

и т. д. Таким образом, при увеличении порядка фильтра время замедления все более приближается к постоянному значению. Время замедления спадает только на 1% его значения 7"(0) на частоте to=2,7ItOc для /г=5 и на частоте а)=3,52й)с для /г= =6 [33].

Поскольку фильтр Бесселя представляет собой полиномиальный фильтр нижних частот, то его передаточная функция аналогична описанным в гл. 2 функциям фильтров Баттерворта и Чебышева. Эту передаточную функцию можно представить в виде произведения функций второго порядка следующего вида:

ДСсо2

Vs

(7.32)

и одной функции первого порядка (если п - нечетно)

(7.33)

7(0)=1М.

(7.28)

Коэффициент усиления звена в каждом случае равен К, а список коэффициентов б и С различных звеньев приведен в приложении Д для порядков п=2, 3, ...

Амплитудно-частотная характеристика фильтра Бесселя монотонно спадает от расположенного на нулевой частоте максимального значения. Следовательно, она имеет сходство с характеристикой фильтра Баттерворта, за исключе.чием того, что крутизна нарастания затухания гораздо меньше. Частота Юс в (7.27)-(7.31) представляет собой не частоту среза, а частоту, определяющую диапазон постоянного времени замедления. Для заданного времени замедления т=Т(ас) можно приблизительной найти частоту tOc или /с=к>с/2зг (Гц) из следующего соотношения:

1 0,15915 f- = =---• (7-34)

Частота среза или частота по уровню 3 дБ для [33]

сОздБ 10,69315 (2п-1). (7.35)

Поскольку фильтр Бесселя представляет собой полиномиальный фильтр нижних частот, то его можно реализовать на основе методик, приведенных в гл. 2. Краткое изложение методик расчета дано в § 7.8.

7.5. ВСЕПРОПУСКАЮЩИЕ ФИЛЬТРЫ С ПОСТОЯННЫМ ВРЕМЕНЕМ ЗАМЕДЛЕНИЯ

Фильтр Бесселя обладает постоянным временем замедления, но его амплитудно-частотная характеристика монотонно спадает с увеличением частоты. Всепропускающий фильтр с постоянным временем замедления, с диапазоном частот, в 2 раза превышающим диапазон фильтра Бесселя [16], имеет следующую передагоч.чую функцию:

Vi KBA-S/2)

(7.36)

где Bn(s) определяется из (7.25) и (7.26). Этот фильтр имеет преимущество над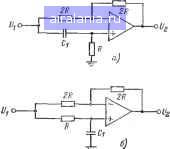

Рис. 7.5 Схемы всепропускающего фильтра

первого порядка:

а - инвертирующий; б - неинвертирующий коэффициент усиления.

фильтром Бесселя, поскольку обладает постоянной амплитудно-частотной характеристикой всепропускающего фильтра.

Передаточную функцию всепропускающего фильтра с постоянным временем замедления можно представить в виде произведения функций второго порядка:

V, К (s - 2Bio,s + 4С<)

s2 -f 2BtOcS + 4Cco

(7.38)

и одной функции первого порядка (если п - нечетно):

У„ К{з-2Сюс) •\/, = S+ 2С(йс

где К - коэффициент усиления звена, а В и С - приведенные в приложении Д коэффициенты фильтра Бесселя.

Передаточную функцию фильтров второго порядка (7.37) можно реализовать с помощью методов, описанных в § 7.2 и 7.3. Для фильтров первого порядка можно использовать схему, изображенную на рис. 7.5. Схема, показанная на рис. 7.5,о, реализует уравнение (7.38) при К=1 и

2Ctoc=l/i?Ci. (7.39)

Следовательно, можно выбрать значение емкости Ci и получить значение сопротивления R из соотношения

R=l/2a)cCCi. (7.40)

Схема, изображенная на рнс. 7.5,6, реализует уравнение (7.38) при инвертирующем коэффициенте усиления К=-1 и идентичными результатами уравнений (7.39) и (7.40). В обоих случаях значе.чие емкости Cil0 c мкФ.

Краткое изложение методики расчета всепропускающего фильтра с постоянным временем замедле.чия приведено в § 7.9.

7.6. РАСЧЕТ ВСЕПРОПУСКАЮЩЕГО ФИЛЬТРА С МНОГОПЕТЛЕВОИ ОБРАТНОЙ СВЯЗЬЮ

Для расчета всепропускающего фильтра второго порядка с заданным фазовьин сдвигом фо на частоте fo (Гц), или <оо= =23tfo (рад/с), и коэффициентом усиления К<1 необходимо выполнить следующие шаги.

1. Если 0<фо<180°, то вычислить

+ Vl + [AK/{l-K)]tgWW} а= 2/Ctg(yo/2)

а если - 180° < ?о < О, то вычислить

-У\ + [4K/(l-/C)]tg4b/2)} 0= 2Ktg{tJ2)

2. Выбрать номинальное значение емкости Ci (предпочтительно близкое к значению 10/fo мкФ) и вычислить значения