

|
|
Главная -> Справочник активных фильтров 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 [21] 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 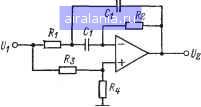 Рис. 7.6. Схема всепропускающего фильтра с МОС. сопротивлений /?2=2/otooCi; Для частного случая К=\/2 использовать при 0<фо<80° 2tg(¥„,2) а при-180°<фо<0 -{ 4 tg= (у„/2) 2tg(¥o/2) В этом случае значения сопротивлений J?2=2/o(aoCi; RiRz/A; ?3=i?4=2i?2- . 3. Выбрать номинальные значения сопротивлений, наиболее близкие к вычисленным значениям, и реализовать схему Б соответствии с рис 7.6. Комментарии а. Для обеспечения лучшей рабочей характеристики номинальные значения элементов должны быть близки к выбранным и вычисленным значениям. Рабочая характеристика фильтра не изменится, если значения всех сопротивлений умножить, а емкостей поделить на общий множитель. б. Входное полное сопротивление ОУ должно быть по крайней мере 10i?eg, где Коэффициент усиления ОУ с разомкнутой обратной связью должен по крайней мере в 50 раз превышать значение амплитудно-частотной характеристики фильтра на частоте fo, а его скорость нарастания (В/мкс) должна в (0,5wo)10- раз превосходить максимальный размах выходного напряжения. в. Коэффициент усиления ограничен" значениями К<1 и приемлемое значение составляет К=1/2. Коэффициент усиления и фазовый сдвиг можно настроить, изменяя соответственно сопротивления Rt и Rs. Всепропускающий фильтр с МОС был рассмотрен в § 7.2. 7.7. РАСЧЕТ БИКВАДРАТНОГО ВСЕПРОПУСКАЮЩЕГО ФИЛЬТРА Для расчета нсепропускающего фильтра второго порядка с заданным фазовым-сдвигом фо на частоте fo (Гц), или ©о= =2nfo рад/с, и коэффициентом усиления 1С необходимо выполнить следующие шаги. 1. Если 0<фо<180°, то вычислить l+/l--4tg4¥o./2) 2tg(y„/2) а при -]80°<фо<0, то вычислить l Kl + 4tg4¥,/2) 2tg(9„ 2) 2. Выбрать стандартное номинальное значение емкости Ci (предпочтительно близкое к значению 10/fo мкФ) и вычислить значения сопротивлений Rs=l/amCi; Ri=R2/2K; Rs=Rh/Ro\ Ri=R5/K, где сопротивление R имеет произвольное-значение и выбирается таким образом, чтобы минимизировать разброс значений сопротивлений. Приемлемое значение составляет R5=R2 и также Rs=R2- 3. Выбрать номинальные значенпя сопротивлений как можно ближе к вычисленным значениям и реализовать схему в соответствии с рис. 7.7. Комментарии а. Комментарии пп. а и б для фильтра с МОС в § 7.6 используются непосредственно, за исключением того, что сопротивление Reg каждого ОУ равно сопротивлению Ri или i?5, соединенного с его инвертирующим входом. б. Инвертирующий коэффициент усиления -К(К>0) задается соотношением KR-JRi. в. Настройка схемы осуществляется следующим образом: изменяя сопротивле-ление Rs, устанавливают фазовый сдвиг,, а сопротивление Ri - коэффициент усиления. На параметр а воздействует изменение сопротивления R-2. Биквадратный всепрспус:;ающий фильтр, был рассмотрен в § 7.3. Рис. 7.7. Схема биквадратного всепропускающего фильтра. 7.8. РАСЧЕТ ФИЛЬТРА БЕССЕЛЯ С ПОСТОЯННЫМ ВРЕМЕНЕМ ЗАМЕДЛЕНИЯ Для расчета фильтра Бесселя или фильтра с постоянным временем замедления с заданным временем замедления т секунд в диапазоне частот 0<f<fc (Гц), или 0<w<toc=2nfc (рад/с), коэффициентом усиления и порядком я=2, 3, ..., 6 необходимо выполнить следующие шаги. 1. Если задано т, то найти частоту fc из соотношения fc=0,I59I5/t. Наоборот, может быть точно задана частота fc, которая определяет t=0,159I5/fc. 2. Найти нормированные коэффициенты В и С из соответствующей графы в приложении Д. 3. Выбрать схему или схемы для реализации фильтра или его звеньев среди Кратко рассмотренных в гл. 2 схем нижних частот. Реализовать фильтр в соответст-гвии с материалом § 2.10-2.12 или 2.13. Комжнтарии а. См. комментарии для схемы филь-ров нижних частот, используемой в гл. 2. б. Время замедления на частоте fc менее заданного значения т. Если требуется, чтобы время замедления на частоте fc было более близко к т, необходимо выбрать фильтр более высокого порядка. Для порядка п-2 время замедления на частоте fc составляет 92,3% значения т, для п=3 99,6%, для п=4 99,99%, а для п=5 или п=6 фактически 100%. Фильтр Бесселя был рассмотрен в 7.4. 7.9. РАСЧЕТ ВСЕПРОПУСКАЮЩЕГО ФИЛЬТРА С ПОСТОЯННЫМ ВРЕМЕНЕМ ЗАМЕДЛЕНИЯ Для расчета всепропускающего фильтра с постоянным временем замедления с заданным временем замедления т, коэф-фициентом усиления К и порядком п- =2, 3, ... 6 необходимо выполнить следующие шаги. I. Найти частоту fc (Гц), или Мс= -2nfc (рад/с), из соотношения fc=0,I5915/t. 2. Найти нормированные коэффициенты В и С из соответствующей графы в приложении Д. 3. Выбрать номинальное значение емкости Ci (предпочтительно близкое к значению 10/fc мкФ). 4. Для фильтра второго порядка или звена второго порядка фильтра более высокого порядка можно использовать а) фильтр с МОС из § 7.6 или б) биквадратный фильтр из § 7.7. Для п. а (фильтр с МОС) неинвертирующий коэффициент усиления К=С/{С+В), а сопротивления /?2=1/В<о<:С,; В В R, = Ri/K; Ri = Для п. б (биквадратный фильтр) коэффициент усиления является инвертирующим -С(С>0) и значения сопротивлений равны /?2=l/2B«)cCi; Ri=Ri/2K; Rs=BWi/Rs; Ri=RblK, где сопротивление Rs имеет произвольное значение и должно выбираться таким образом, чтобы минимизировать разброс значений сопротивлений. 5. Если фильтр имеет нечетный порядок, то кроме звеньев второго порядка будет присутствовать одно звено первого порядка, соответствующее звену первого порядка из приложения Д с коэффициентом С. Неинвертирующий коэффициент усиления, равный 1, можно реализовать, если использовать схему, изображенную на рис. 7.5,а, а инвертирующий коэффициент усиления - схему, приведенную на рис. 7.5,6. В обоих случаях i?=l/2a)cCCi. 6. Выбрать номинальные значения сопротивлений, более близкие к вычисленным значениям, и реализовать фильтр или его звенья в соответствии со схемой, приведенной на рис. 7.5, 7.6 или 7.7. Комментарии См. соответствующие комментарии в § 7.6 нли 7.7. ПРИЛОЖЕНИЯ Приводимые приложения содержат исходные данные для расчета нормированных фильтров Баттерворта, Чебышева; инверсных Чебышева, эллиптических и Бесселя нижних частот. Передаточные функции можно представить в виде произведения функций звеиьев второго порядка, а для фильтров нечетного порядка как сомножитель входит функция одного звена первого порядка. Для фильтров Баттерворта, Чебышева и Бесселя функция звена второго порядка определяется следующим образом: V, КСшК У, - BwsS + Сыс Для инверсных Чебышева и эллиптических фильтров функция звена этого порядка имеет вид: [КС/А) (s + Ai:) Функция звена первого порядка фильтров типа Баттерворта, Чебышева, инверсного Чебышева, эллиптического и Бесселя задается в виде У2- КСыд У, ~ s + Cc • В каждом случае К представляет собой коэффициент усиления звена, а Мс-частота среза фильтра, за исключением фильтра Бесселя, где на частоте а)с=время замедления равно приблизительно I/wc(c). Для нормированного фильтра Wc=l) коэффициенты А, В к С приведены в строках таблиц приложений. Каждая строка описывает звено, а для звена первого порядка приводится только значение С. Ис- ходные данные располагаются в соответствии с порядком фильтра Л. Исходные данные фильтров Баттерворта и Чебышева приведены в приложении А, в котором представлен перечень коэффициентов в и С. Неравномерность передачи в полосе пропускания PRW для фильтра Чебышева равна 0,1; 0,5; I; 2 и 3 дБ, а порядки выбраны Л=2, 3, ..., 10. Исходные данные инверсных фильтров Чебышева приведены в приложении Б. Дан перечень коэффициентов А, В к С для различных значений минимального затухания в полосе задерживания MSL, выраженного в децибелах. Параметры WZ, WM и КМ используются при настройке звеньев фильтра в соответствии с методикой, описанной в § 3.6. Указаны следующие порядки N= =2, 3, ..., 10. В приложении В приведены исходные данные эллиптических фильтров. Приложение В аналогично приложению Б, за исключением того, что добавлены нормированные значения ширины переходных областей TW. Для каждого порядка (2, 3, 10) исходные данные распределены в соответствии с неравномерностью передачи в полосе пропускания PRW, равной 0,1; 0,5; 1; 2 и 3 дБ. В приложении Г указаны нормированные значения ширины переходных областей TW эллиптических фильтров с заданными неравномерностью передачи в полосе пропускания PRW, минимальным затуханием в полосе задерживания MSL и порядком ЛГ. Для каждого значения PRW (0,1; 0,5; 1; 2 или 3 дБ) строки таблицы дают значения TW в зависимости от MSL, а порядок ЛГ определяет соответствующую колонку. Коэффициенты фильтров Бесселя В и С приведены в таблице приложения Д для для 1ЛГ=2, 3, ..., 6. 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 [21] 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 0.0128 |