среза или граничную точку полосы, частот с пульсациями. Если интересуются значением частоты со здБ, т. е. точкой, в которой характеристика спадает lih 3~ йБ, то получают [16]

arch-

)•

(2.11)

Следует отметить, что <Вс=Шзд5, если

е=Г, и в этом случае получаем фильтр Чебышева с неравномерностью передачу 3 дБ.

Передаточные функции фильтров Чебышева нижних частот по форме идентичны функциям фильтра Баттерворта, определенным ранее уравнениями (2.2)-(2.4). Полиномы знаменателя для произведений сомножителей (2.3) и (2.4) табулированы и для сйс=1 рад/си я=2, 3, ..., 10 приведены в приложении А для неравномерности передачи в полосе пропускания 0,1; 0,5; 1; 2 и 3 дБ- •

1,0. .1,5 2,0 и1,рар,/с г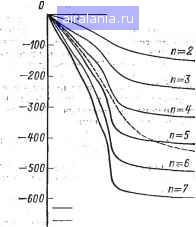

-Чебышева fs=0,B) - Баттерворта (пВ)

Рис 2.9. Фазо-частотные, характеристики фильтров Баттерворта и Чебышева.

Рис. 2.10. Амплитудро,-частот.ная характе--ристика реального фильтра, Чебышева четвертого, п,орядкз.,

Амплитудно-частотная характеристика фильтра Чебышева данного порядка лучше амплитудно-частотной характеристики Баттерворта, так как у фильтра Чебышева уже ширэна переходной области. Однако фазо-частбтная характеристика фильтра Чебышева хуже (более нелинейна) по сравнению С: фазо-частотной характеристикой фильтра Баттерворта. Фазо-частотные характеристики фильтра Чебышева для 2-7-го порядков приведены на рис. 2.9. Для сравнения на рис.. 2.9 штриховой линией изображена фазо-чаСтотная характеристика фильтра Баттерворта шестого порядка. Можно также отметить, что фазо-частотные характеристики. фильтров Чебышева высокого до-рядка хуже фазо-частотных характеристик фильтров более низкого порядка. Это согласуется с тем фактом, что амплитудно- . частотная характеристика фильтра Чебышева высокого порядка лучше амплитудно-частотной характеристики фильтра более низкого порядка.

Амплитудно-частотная характеристика реального фильтра Чебышева четвертого порядка с неравномерностью передачи 1 дБ показана на рис. 2.10.

2.4, ВЫБОР МИНИМАЛЬНОГО ПОРЯДКА

На основе рис. 2.6 и 2.8 можно сделать вывод, что чем выше порядок фильтров Баттерворта и Чебышева, тем лучше их амплитудно-частотная характеристика. Однако более высокий порядок усложняет схемную реализацию и вследствие этого повышает стоимость. Таким образом, для разработчика представляет интерес выбор минимально необходимого порядка фильтра, удовлетворяющего заданным требованиям.

Другими словами, предположим, что в изображенной на рис. 2.2 общей характеристике заданы максимально допустимое затухание в полосе пропускания аг (дБ), минимально допустимое затухание в полосе задерживания Сг (дБ), частота среза сОс (рад/с) или /с (Гц) и максимальная допустимая ширина переходной области TW, которая определяется следующим образом:

TW=(o,-СОс.

(2.12)

(Следовательно, полоса задерживания должна начинаться с некоторой частоты <02<cui.) Задача состоит в нахождении минимального порядка п, который будет удовлетворять всШ этим условиям.

Для фильтраБаттерворта с 01 = 3 дБ минимальный порядок можно определить, подставив приведенные выше условия в (2.1) и решив его относительно порядка п. в результате получаем

log(№°-1) 2 log (со,/(Ос)

где логарифмы могут быть или натуральными, или десятичными.

(2.13)

Уравнение (2.12) можно записать а виде

co,/cuc=(TW/cuc)--l (2.14)

и пюлученное соотношение подставить а (2.13) для нахождения - зависимости порядка п от ширины переходной области, а не от частоты сО]. Параметр TW/oic называется нормированной шириной переходной области и является безразмерной величиной. Следовательно, TW и Юс можно задавать и в радианах на секунду, и в герцах.

Подобным же образом на основе (2.6) для К=1 найдем минимальный порядок фильтра Чебышева

arch V (10"/0-1)/(10"-/0-1)

arch (и,/лЗс)

(2.15)

Уравнение (2.14) снова можно использовать для исключения частоты соь

В качестве примера предположим, что заданы «1=3 дБ, «2=20 дБ, fc=1000 Гц, а ширина переходной области TW не должна превышать 300 Гц. Из (2.14) получаем

сй,./сйе=(300/1000)--1=1,3,

а из (2.13) следует, что удовлетворяющий этим требованиям фильтр Баттерворта должен иметь следующий минимальный порядок:

log (10==-1)

21og,„1.3 =6-

Поскольку порядок должен быть целым числом, то берем ближайшее большее целое число: и=9.

Минимальный порядок фильтра Чебышева, удовлетворяющего этим требованиям, находится из (2.15):

archK(10=-l)/(2-l)

" =-ШГй-= 39S-

Снова находя ближайшее большее целое число, получаем и=4.

Этот пример наглядно иллюстрирует преимущество флльтра Чебышева над фильтром Баттерворта, если основным параметром является амплитудно-частотная характеристика. В рассмотренном случае фильтр Чебышева обеспечивает ту же самую крутизну передаточной функции, что и фильтр Баттерворта удвоенной сложности.

Уравнения (2.13) и (2.15) можно также использовать для нахождения ширины лереходной области TW фильтров Баттерворта и Чебышева фиксированного порядка. Например, подставляя уравнение (2.14) в (2.13) и решая его относительно TW/cOc, получаем

TW 2п/-

- = YiO-l - l (2.16)

для фильтра Баттерворта. Повторяя эту процедуру с уравнением (2.15), получаем для фильтра Чебышева

=ch(-arch/

10"/о 1 \

- 1.

(2.17)

Для иллюстрации использования этих формул найдем ширину переходной области TW фильтра Баттерворта из предыдущего примера для ai=3 дБ (рассматривается только фильтр Баттерворта), =20 дБ, fc=IOOO Гц-и п=9. Из (2.16) находим

Ш=99-1=0,2Ш

и, следовательно, TW=0,29lcuc рад/с "или 0,291/"с=291 Гц. Этот результат согласуется с предыдущим примером, в котором было показано, что TW300 Гц.-

2.5. ФИЛЬТРЫ НИЖНИХ ЧАСТОТ "С МНОГОПЕТЛЕВОИ ОБРАТНОЙ СВЯЗЬЮ И БЕСКОНЕЧНЫМ КОЭФФИЦИЕНТОМ УСИЛЕНИЯ

Существует много способов построения активных фильтров нижних частот Баттерворта и Чебышева. Далее будут рассмотрены некоторые из наиболее применяемых в настоящее время общих схем, начиная с простых (с точки зрения числа необходимых схемных элементов) и переходя к наиболее сложным.

Для фильтра нижних частот второго порядка с частотой среза сОс типовая полиномиальная передаточная функция имеет следующий вид:

(2.18)

Постоянные В и С представляют собой вормированные коэффициенты, поскольку для сйс=1 эта передаточная функция приводится к виду (2.2) при п=2. Для фильтров Баттерворта и Чебышева эти коэффициенту приведены в приложении А. Постоянная К определяет коэффициент усиления, который, конечно, также необходимо точно задать.

Для фильтров более высокого порядка уравнение (2.18) описывает передаточную функцию типового звена второго порядка, где К - коэффициент его усиления; В и С - коэффициенты звеиа, приведенные в приложении А.

Одна из наиболее простых схем активных фильтров, реализующих передаточную функцию нижних частот согласно (2.18), приведена на рис. 2.11 [3]. Она иногда называется схемой с многопетлевой обратной связью (МОС) и бесконечным коэффициентом усиления из-зг наличия двух путей прохождения сигнала обратной связи через

-f--l-

о г

Рис. 2.11. Схема фильтра нижних частот с мое второго порядка

Элементы Ci и R, а также вследствие того, что ОУ в этом случае работает как прибор с бесконечным коэффициентом усиления. (Пример фильтра, на усилителе с конечным коэффициентом усиления рассмотрен в следующем параграфе.) Эта схема реализует уравнение (2.18) с инвертирующим коэффициентом усиления - К (К>0) и

С(о=

(2.19)

нению

Сопротивления, удовлетворяющие урав-(2.19), равны

Rr = R,/K; i?3= l/CC,C4>%R,,

(2.20)

где значения Ci и Сг выбираются произвольно. Сопротивления задаются в омах, а емкости - в фарадах.

Следовательно, по заданным К, В, С и СОс можно выбрать значения Ci и Сг и вычислить требуемые значения сопротивлений. Емкости должны иметь номинальные значения, которые в результате расчета дают реальное значение сопротивления Ri. Это условие выполняется, если

C,B2C2/[4C(K-fl)]. (2.21)

Целесообразный подход состоит в том, чтобы задать номинальное значение емкости Сз, близкое к значению 10/fc мкФ и выбрать наибольшее имеющееся номинальное значение емкости d, удовлетворяющее уравнению (2.21). Сопротивления должны быть близки к значениям, вычисленным по (2.20). Чем выше порядок фильтра, тем более критичными являются эти требования. Если в наличии отсутствуют вычисленные номинальные значения сопротивлений, то следует отметить, что все значения сопротивлений можно домножить на общий коэффициент при условии, что значения емкостей делятся на тот же самый коэффициент.

В качестве примера предположим, что необходимо разработать фильтр Чебышева с мое второго порядка с неравномерностью передачи 0,5 дБ, полосой пропускания 1000 Гц и коэффициентом усиления равным 2. в этом случае К=2, Шс=2я(1000), а из приложения А находим, что В= 1,425625 и С=1,516203. Выбирая номинальное значение Cs=10/fc=10/1000=0,01 мкФ=10-8 Ф,. из (2.21) получаем

(1,425625)=-0,01 < 4.1.516203-3 = ООО"

Выберем номинальное значение емкости Ci=0,001 мкФ=1 нФ и вычислим по (2.20) значения сопротивлений. В результате

23

[ 1,425625 -Ю-" -4-/(1,425625)=-10-«- -4-1,516203.10-9.10--3] 2000я== = 0,506-10 Ом = 50,6 кОм; Ri = 50,6/2 = 25,3 кОм

п !

»- l,516203-10--10-(20007t)=•50,6-I0=~ =0,330•10= Ом=33 кОм.

В заключительном примере предположим, что необходимо разработать фильтр Баттерворта шестого порядка с МОС, частотой среза fc=1000 Гц и коэффициентом усиления /С=8. Он будет состоять из трех звеньев второго порядка, каждое с передаточной функцией, определяемой уравнением (2.1). Выберем коэффициент усиления каждого звена К=2, что обеспечивает требуемый коэффициент усиления самого фильтра 2-2-2=8. Из приложения А для первого звена находим 6=0,517638 и С=1. Снова выберем номинальное значение емкости С2=0,01 мкФ и в этом случае из (2.21) найдем Ci0,00022 мкФ. Зададим номинальное значение емкости Ci=200 иФ к. из (2.20) найдем значения сопротивлений /?2=139,4 кОм; i?i = 69,7 кОм; /?з=90,9 кОм.

Два других звена рассчитьшаются аналогичным способом, а затем звенья соединяются каскадно для реализации фильтра Баттерворта шестого порядка. Результирующая схема имеет амплитудно-частотную характеристику, показанную ранее на. рис. 2.7.

Из-за своей относительной простоты фильтр с МОС является одним из наиболее популярных типов фильтров с инвертирующим коэффициентом усиления. Он обладает также определенными преимуществами, а именно хорошей стабильностью характеристик и низким выходным полным сопротивлением [9]; таким образом, его можно сразу соединять каскадно с другими звеньями для реализации фильтра более высокого порядка. Недостаток схемы со-