стоит в том, что невозможно достичь высокого значения добротности Q без значительного разброса значений элементов и высокой чувствительности к их изменению. Для достижения хороших результатов коэффициент усиления К и добротность Q должны быть ограничены значением, приблизительно равным 10. Коэффициент усиления может быть больше, если значение добротности выбрано меньшим и выполняется ограничение, например: KQ = 100 при

Из (1.11) можно установить, что добротность Q определяется соотношением Q= -VC/B. В фильтре Баттерворта нижних частот шестого порядка первое звено имеет наибольшее значение добротности Q=l/0,517638=1,93 (см. приложение А). Следовательно, в этом примере можно обоснованно применять фильтр с МОС, получая достаточно хорошие результаты.

Краткое изложение методики расчета фильтра с МОС и практические рекомендации даны в § 2.10.

2.6. ФИЛЬТРЫ НИЖНИХ ЧАСТОТ НА ИНУН

На рис. 2.12 (26] приведена широко распространенная схема фильтра нижних частот второго порядка, реализующая не-инвертирующий (положительный) коэффициент усиления. Эта схема иногда называется фильтром на ИНУН, поскольку ОУ и два подсоединенных к нему резистора Rs и Ri образуют источник напряжения, управляемый напряжением (ИНУН).

Эта схема реализует функцию фильтра нижних частот второго порядка (2.18) с параметрами:

Сч>%= l/R,RC,C;

1/1 IN

Ki=l+RJR,.

(2.22)

Величина [xl представляет собой коэффициент усиления ИНУН, а также и коэффициент усиления фильтра. Удовлетворяющие уравнению (2.22) значения сопротивлений определяются следующим образом:

~[ВС, +V[B+iC{K-l)]x

R,= l/CC,CR,cc; R,K(R, + R2)/{K-R, = K{R, + R,),

(2.23)

где значения С, и Cs выбираются. Сопротивления Rs и 4 задаются таким образом, чтобы минимизировать смещение по постоянному току ОУ. (Напомним, что в идеальном случае напряжение смещения между входными выводами должно быть равно нулю).

Если требуется К=1, то значения Ri и i/?2 также определяются из (2.23), но в этом случае получаем Rs=oo (разомкнутая цепь) к Ri=0 (короткозамкнутаяцепь). Для минимизации смещения по постоянному току должно выполняться условие i?4= =?1+2. но в большинстве некритических применений будет достаточна короткоза-мкнутая цепь. В этом случае ИНУН работает как повторитель напряжения, т. е. его выходное напряжение равно входному илн повторяет его.

Расчет фильтра на ИНУН производится так же, как и расчет для фильтра с МОС в § 2.5. Номинальное значение емкости Сг выбирается близким к значению lO/fc мкФ, а номинальное значение емкости Си удовлетворяющим неравенству

CiIB2--4C(K-1)]С2/4С. (2.24)

(Это гарантирует вещественное значение 1.) Значения сопротивлений находятся затем из (2.23) с приведенной выше модификацией при К=1.

Как было подчеркнуто ранее, фильтр на ИНУН позволяет добиться неинверти-рующего коэффициента усиления при минимальном числе элементов. (Для него требуется только на один резистор больше, чем для фильтра с МОС.) Он обладает низким полным выходным сопротивлением, небольшим разбросом значений элементов и возможностью получения относительно высоких значений коэффициента усиления. Кроме того, этот фильтр относительно прост в настройке. Точная установка коэффициента усиления осуществляется, например, с помощью подстройки сопротивлений

и Ri потенциометром. Однако подобно фильтру с МОС фильтр на ИНУН должен использоваться для значений добротности Q<10.

Полная методика расчета приведена в § 2.11.

2.7. БИКВАДРАТНЫЕ ФИЛЬТРЫ НИЖНИХ ЧАСТОТ ,

В заключение рассмотрим фильтр нижних частот второго порядка, реализующий передаточную функцию (2.18) на основе изображенной на рнс 2.13 [31] биквадратной схемы. Хотя эта схема содержит больше элементов, чем схемы с" МОС и на ИНУН, по характеристикам она лучше и имеет преимущества за счет простоты настройки и лучшей стабильности. Сравнительно просто реализуются значения добротности Q. вплоть до 100, и относительно легко формируются фильтры высокого порядка на основе каскадного соединения нескольких биквадратных звеньев.

-oVp

Рис. 2.12. Схема фильтра нижних частот на ИНУН второго порядка.

Эта схема реализует уравнение (2.18) при неинвертирующем коэффициенте усиления К и

Cco=c=l/i?3/?4CS; B(Oc=l/i?sC,; (2.25)

Значении сопротивлений определяются из следующих соотношений:

/?2= 1/£С,(0с; (2.26)

i?3=l/CC>/?,

где Cl и Ri выбираются. Если значение С] выбрано близким к iO/fc мкФ, то прием-лимое значение R равно

Й4=1/<0сС,, (2.27)

в этом случае получаем:

RRJKC; • R2=RJB: (2.28)

R, = RJC.

Из (2.28) следует, что биквадратная схема относительно легко настраивается. Для выбранного значения Rt изменение /?2 приводит к изменению коэффициента В, а изменение Rz - коэффициента С. Затем при правильно установленном значении коэффициента С с помощью изменения Ri задается коэффициент усиления К-

Если же требуется инвертирующий коэффициент усиления, то выходной сигнал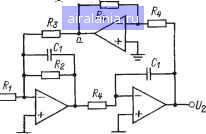

Рис. 2.13. Схема биквадратного фильтра нижних частот второго порядка.

Vi можно снимать с узла а, сохраняя зна-. чения элементов такими же, как и раньше.

Полная методика расчета приведена в § 2.12.

2.8./НАСТРОИКА ФИЛЬТРОВ ~ ВТОРОГО ПОРЯДКА

Настройку фильтра второго порядка или звена второго порядка фильтра более высокого поридка можно осуществить намного проще, если разработчику известен общий вид характеристики. Для функции фильтра нижних частот второго порядка! (2.18) амплитудно-частотная характеристика будет иметь максимальное значение Km, расположенное на частоте fm при условии, что В1С<2. Вид такой характеристики изображен на рис. 2.14,а, а значения Km и fm определяются следующим образом:

Km = 2СК/В V4C- В=; (2. 2

(2.30>

Подъем амплитудно-частотной характеристики происходит при выполнении условия <?> 1 2=0,707. Если же <3<0,707 (или BVC>2), то подъем отсутствует и вид характеристики показан на рис. 2.14,6. На обоих рисунках fc - частота среза фильтра, а соответствующее ей значение амплитудно-частотной характеристики равно

Кс = КС/У (0-1)+ В\ (2.31>

В качестве примера рассмотрим фильтр Баттерворта четвертого порядка с частотой среза 1000 Гц и коэффициентом усиления каждого звена, равного 2. Из приложения А найдем для первого звена: 5=0,765367 и С-\. Следовательно, иа уравнения (2.29) получаем

= fc Ус-(В72).

Km =:

2-1.2

(0.765367)== 1 --о-= 841 Гц.

0,765367 К 4-1 -(0,765367)= = 2.8284.

а из (2.30)

f„= 1000/

На частоте fc из (2.31) находим значение амплитудно-частотной характеристики

Кс = 2. \/V(\ - 1)2 + (0.765367)= = 2,6131..

что соответствует затуханию 3 дБ.

Вследствие этого амплитудно-частотная характеристика должна быть подобна характеристике, приведенной на рис. 2.14,а-(поскольку С= 1/0,765367= 1,31). Максимальное значение на частоте 841 Гц равно 2,8284, а на частоте 1000 Гц -2.6131. При этом на постоянном токе значение амплитудно-частотной характеристики равно 2.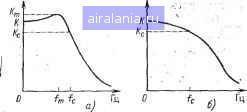

Рис. 2.14. Амплитудно-частотные характеристики фильтра нижних частот:

а -О>0,707; б - QO.m.

Для второго звена находим, что В= = 1,847759 и С=1. Следовательно, Q = = 1/В=0,54 и сама характеристика будет иметь вид, подобный характеристике на рис. 2.14,6, при К=2 значение амплитудно-частотной характеристики на частоте 1000 Гц равно

Кс= 2.1/У(1 - 1)= -f (1,847759)= = 1,0824.

В качестве проверки заметим, что при каскадном соединении двух звеньев значение амплитудно-частотной характеристики на частоте О равно 2-2=4, а на частоте 1000 Гц составит 2,6131X1,0824= =2,828. Последнее значение равно 0,707-4, как и следовало ожидать.

Рекомендации по настройке различных типов фильтров приведены в методиках их расчета в § 2.10-2.12.

2.9. ФИЛЬТРЫ НЕЧЕТНОГО ПОРЯДКА

Для фильтров Баттерворта и Чебышева нечетного порядка одно звено должно обладать передаточной функцией первого порядка вида первого сомножителя в (2.4). Для обобщенной частоты среза о)с= =2я/с (рад/с) этот сомножитель первого порядка определяется следующим образом:

V2/l/,=/CCcuc/(s-f-Ccuc), (2.32)

где К - коэффициент усиления звена, а С задается как коэффициент звена 1 в приложении А.

Схема, с помощью которой осуществляется реализация функции (2.32) при К>\, приведена на рис, 2.15. Значение емкости С] должно выбираться близким к значению 10 с, мкФ, при этом значения сопротивлений

i?,= l/cocC,C;

RKRJ(K-\y, (2.33)

R, = KR,.

Если желательно получить коэффициент усиления /С=1, то в качестве звена первого порядка можно использовать схе-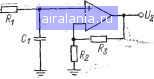

Рис. 2.15. Схема"фильтра нижних частот первого порядка.

-о и.

Рис. 2.16. Схема звена нижних частот первого порядка с единичным коэффициентом усиления.

му, приведенную на рис. 2.16. В этом слу чае находнтся из (2.33), а Ci снова выбирлется.

В качестве примера предположим, что необходимо реализовать фильтр Баттерворта третьего порядка с частотой fc-= 1000 Гц и коэффициентом усиления. К=2. Из приложения А находим, что для звена первого порядка в (2.32) С=], а для звена второго порядка в (2.18) В= = С=1. Выберем коэффициенты усиления для звена первого порядка К=1, а для звена второго порядка К=2. Следовательно, звено первого порядка реализуется схемой, показанной на рис. 2.16. Выбирая номинальное значение емкости С,= =0,01 мкФ, из первого соотношения уравнения (2.33) получаем

Ri==2GO(\o-s.iOul5.9lZyOM.

Звено второго порядка можно реализовать для неинвертирующего коэффициента усиления с помощью методики, приведенной в § 2.6 или 2.7, а для инвертирующего коэффициента усиления - в § 2.5.

(2.10. РАСЧЕТ ФИЛЬТРА НИЖНИХ ЧАСТОТ С МНОГОПЕТЛЕВОИ ОБРАТНОЙ СВЯЗЬЮ

Для расчета фильтра нижних частот второго порядка или звена второго порядка фильтра Баттерворта или Чебьш1ева более высокого порядка, обладающего заданной частотой среза fc (Гц) или сйс = =2зх/с (рад/с) и коэффициентом усиления К, необходимо выполнить следующие шаги.

1. Найти нормированные значения коэффициентов В и С из соответствующей таблицы в приложении А.