Рис. 3.2. Амплитудно-частотная характеристика реального инверсного фильтра Чебышева шестого порядка.

Если «2=-20 logio2 представляет еобой минимальное затухание в полосе задерживания (дБ), то

!=l/"/lO"=/°-1.

(3.4)

Следовательно, для заданного порядка- п, минимального допустимого затухания в полосе задерживания и частоты (Qi (начала полосы задерживания, содержащей пульсации) можно из (3.4) найти значение 8, а нз (3.1) требуемую амплитудно-частотную характеристику. Тогда частоту среза «с и ширину переходной области можно определить из (3.2) и (3.3). Наоборот, можно точно установить частоту «с (легче, чем coi) и из (3.2) найти частоту Оь

Амплитудно-частотная характеристика лабораторного образца инверсного фильтра Чебышева приведена на рис. 3.2. Минимальное затухание в полосе задерживания составляет 20 дБ.

Минимальный порядок п, требуемый для обеспечения заданных технических требований «2, сОс и coi из (3.2) и (3.4), определяется следующим образом:

arch 1/10"=/°-1

arcn у - - I

Соотношение между шириной переходной области TW и отношением частот toi/coc находится из (3.3) и равно

«,/(Oe=(TW/cOc)--l. (3.6)

Из (3.5) и (3.6) можно также получить нормированную ширину переходной области

«с

= zb(&KbV\Ql-\ -1.

(3.7)

Следовательно, видно, что для более узкой переходной области требуется большее значение порядка п, что связано с увеличением числа пульсаций.

В качестве примера предположим, что надо найти минимальный порядок, необходимый для реализации 02=20 дБ, fc = =Шс/2я=1000 Гц и TW<300 Гц. Из (3.6) находим Ш1/шс=1,3, так что из (3.5) требуемый порядок

arch Kl02- 1 "=-arch 1.3 =3-Q5-

Таким образ9м, минимальный порядок п=4, который обеспечивает TW<300 Гц. Точное значение находится из (3;7)

TW = 1С00

arch -

.= 292.

Данный пример рассматривался в § 2.4 для фильтра Чебышева и привел к идентичным результатам. Этот факт иллюстрирует общее положение, а именно что для заданных допустимых отклонений в полосах пропускания и задерживания и частот tOc и TW фильтры Чебышева и инверсный Чебышева имеют одинаковый порядок, который, в свою очередь, меньше требуемого порядка фильтра Баттерворта. Таким образом, если требуется монотонная характеристика в полосе пропускания, то инверсный фильтр Чебышева по параметрам превосходит фильтр Баттерворта того же порядка. Если же можно допустить пульсации в полосе пропускания, то лучше фильтр Чебышева, поскольку, как увидим в дальнейшем, его передаточная функция проще, чем у инверсного фильтра Чебышева. Однако, если желательна монотонная характеристика, хорошие результаты дает часто и фильтр Баттерворта, поскольку его передаточная функция также проще, чем инверсного фильтра Чебышева.

Передаточная функция инверсного фильтра Чебышева имеет вид, описываемый общим уравнением (1.6). Следовательно, этот фильтр в общем случае более сложен в реализации, чем полиномиальные фильтры, такие, как фильтры Баттерворта и Чебышева. В виде произведения сомножителей функция инверсного фильтра Чебышева нижних частот четного порядка п записывается следующим образом:

(S.8)

а нечетного порядка п (п-1) /2

где Ло, Со, Ai Oi, bi и Ci - заданные постоянные числа.

Для удобства читателя в таблицах приложения Б приведены передаточные функции инверсного фильтра Чебышева нижних частот для нормированного случая (шс=1 рад/с). Таблицы соответству-

ют порядкам п=2, 3, ..., 10 и в большинстве случаев даны минимальные пульсации в полосе задерживания от 30 до 100 дБ с шагом 5 дБ. Каждый сомножитель в (3.8) или (3.9) соответствует функции фильтра при п=2 или функции звена при п>2. Исходные данные заданной передаточной функции определенного порядка п (обозначенного как Л?) и с минимальным затуханием в полосе задерживания (MSL) сгруппированы вместе. Для сомножителей второго порядка коэффициенты Яг, bi и с,- (обозначенные как А, В и С) расположены в строках. Первая строка соответствует первому сомножителю, вторая строка - второму сомножителю и т. д. Для фильтра нечетного порядка (3.9) коэффициент Со обозначается как С и приводится в последней строке исходных данных. Колонки WZ, WM и КМ используются при настройке фильтра и будут рассмотрены в § 3.6.

Постоянные числа Ло и Л, связаны с коэффициентом усиления фильтра или одного из его звеньев. Например, если Ki представляет собой коэффициент усиления звена второго порядка, то Kt определяет значение сомножителя второго порядка при 5=0 и задается следующим образом:

Кг=АгШ/с1.

Следовательно, получаем

Аг=КгСг/аи (3.10)

Для звена первого порядка, соответствующего сомножителю первого порядка уравнения (3.9), его коэффициент усиления Ко определим из соотношения Ко= =Ао/Со и, таким образом, получим

Ао=КоСо.

(3.11)

В качестве примера предположим, что необходима передаточная функция инверсного фильтра Чебышева пятого порядка с С0с=1 рад/с, коэффициентом усиления /С=8 и минимальным затуханием в полосе задерживания MSL=40 дБ. Из приложения Б находим для первого звена второго порядка

Л=2,887037; В=0,503909;

С= 1,037939;

для второго звена второго порядка

Л=7,558361; В=1,696117;

С= 1,334444

и для звена первого порядка

С= 1,273011.

3.2. ЭЛЛИПТИЧЕСКИЕ ФИЛЬТРЫ

Как было показано в гл. 2, эллиптический фильтр имеет амплитудно-частотную характеристику, которая содержит пульсации как в полосе пропускания, так и в полосе задерживания и является луч-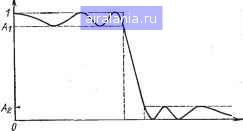

Рис. 3.3. Амплитудно-частотная характеристика эллиптического фильтра нижних частот для случая п=5.

шим среди всех фильтров нижних частот в том смысле, что для заданного порядка и допустимых отклонений характеристики в полосах пропускания и задерживания обладают самой узкой шириной переходной области. Пример амплитудно-частотной характеристики эллиптического фильтра пятого порядка изображен на рис. 3.3.

Пульсации в полосе пропускания равны по значению и могут характеризоваться максимальным допустимым затуханием и полосе задерживания. Эта величина, которую мы также будем называть не-равномерностью передачи в полосе пропускания (PRW), дБ, согласно обозначению на рис. 3.3 равна

PRW=-20 logioA,. (3.12)

Пульсации в полосе пропускания также равны по значению (хотя не обязательно равны размаху пульсаций в полосе пропускания) и характеризуются минимальным затуханием в полосе задерживания (MS.L), дБ, следующим образом:

MSL=-20 1од,оЛ2. (3.13)

Ширина переходной области TW, как и для других типов фильтров, составляет

TW=co,-СОс. (3.14).

Для заданных значений PRW и MSL. повышение порядка приводит к увеличению числа пульсаций в полосах пропускания и задерживания и уменьшению TW. Следовательно, можно задать обозначенные на рис. 3.3 параметры Аи Лг и сйс и,. увеличивая порядок, достичь любого требуемого значения coi>coc.

Для иллюстрации преимуществ эллиптического фильтра рассмотрим рис 3.4. На нем изображены две кривые, показывающие зависимость порядка фильтров Чебышева и эллиптических от ширины переходной области. Рассмотрен случай с неравномерностью передачи в полосе пропускания 0,1 дБ и минимальным затуханием в полосе задерживания 60 дБ при частоте среза 1 рад/с. Другие случаи дают аналогичные результаты.

40 35

I-го

10 1,0 0,10 0,01 Нормированная ширина-Переходной области

Рис. 3.4. Зависимость порядка фильтров Чебышева (2) и эллиптических (1) от ширины переходных областей для PRW=0,1 и MSL=60 дБ.

В качестве примера применения рис. 3.4 предположим, что необходимо обеспечить ширину нормированной переходной области не более 0,1. Другими словами, если иметь в виду рис. 3.4 с <йс= 1, то необходимо, чтобы coi была ми1ьше или равна 1,1. Из рис. 3.4 следует, что подходит эллиптический фильтр с порядком 10. (Для обеспечения ширины 0,1 требуется значение п между 9 и О, и следовательно, выбирают п=10.) Однако для фильтра Чебышева потребуется минимальный порядок, равный 22. Преимущество эллиптического фильтра над фильтром Чебышева еще более заметно при узкой ширине переходных областей. Например, если ширина не превосходит 0,03, то достаточно использовать эллиптический •фильтр 12-го порядка, а минимальный порядок фильтра Чебышева будет 39.

Передаточная функция эллиптического фильтра по форме идентична передаточной функции инверсного фильтра Чебышева, определенной ранее уравнениями (3.8) и (3.9) [16]. Постоянные параметры а,, bi и Сг, которые отличаются от параметров инверсного фильтра Чебышева, вьиис-ляются крайне сложно. Этот процесс требует знания эллиптических функций Якоби-[И].

Для удобства читателя передаточные функции в виде произведения сомножителей приведены в таблицах приложения В для нормированного случая (<Вс=1 рад/с) и порядков-«=2, 3, 10. Они даны для пульсаций в полосе пропускания 0,1; 0,5; 1; 2 и 3 дБ и для большинства случаев приведены минимальные пульсации в полосе задерживания от 30 до 100 дБ с шагом 5 дБ. Для каждого случая указана соответствующая ширина переходной области.

а именно ее нормированное значение

COl-1.

Исходные данные передаточной функции с определенным порядком .n=N, неравномерностью передачи в полосе пропускания (PiRW) и минимальным затуханием в полосе задерживания (MSL) сгруп= пированы под заголовком Л и PRW. В этой группе находят исходные данные для заданного значения MS-L, вынесенного в первую колонку. Для сомножителей второго порядка вида ([3.8) его коэффициенты Яг, bi и d (обозначенные как А, В и С) приведены в строках. Первая строка соответствует первому сомножителю, вторая строка - второму сомножителю и т. д. Для сомножителя первого порядка (для нечетного Л), а именно вида Ao/{s+co) (3.9), коэффициент Со обозначен как С и приведен в последней строке этих исходных данных. Данные в колонке TW указывают результирующую ширину нормированной переходной области, а данные в колонках WZ, WM f КМ используются прп настройке фильтра. Они будут рассмотрены в § 3.6.

Постоянные числа Ао и Л, определяют требуемый коэффициент усиления, как и для инверсного фильтра Чебышева, рассмотренного в § 3.1.

В качестве альтернативы может потребоваться нахождение передаточной функции минимального порядка N с заданными PRW, MSL и максимально допустимой шириной переходной области TW. Это можно осуществить с помощью данных приложения Г, в котором приведены значения TW для каждого эллиптического фильтра. Необходимо только найти наименьший порядок N, которому соответствует не превосходящая заданного значения TW ширина переходной области. В обоих приложениях В и Г приведены нормированные значения TW (сОс=1 рад/с), которые необходимо домножить на заданную частоту СОс. Другими словами, приведенная ширина переходных областей в

Рис. 3.5. Амплитудно-частотная характеристика реального эллиптического фильтра нижних частот пятого порядка.