41)0-

-czi-I

-Ot/2

Рис. 3.15. Схемы фильтров нижних частот первого порядка.

и неравномерностью передачи в полосе нро-шускания (PRW), необходимо выполнить следующие шаги.

1 Найти нормированное значение коэффициента С звена первого порядка из

соответствующей таблицы в приложении В или Г.

2. Выбрать номинальное значение емкости Cl (предпочтительно близкое к значению 10/fc мкФ).

За. Если К>\, использовать приведенную на рис. 3.15,а схему, для которой значения сопротивлений равны

i?i=l/cocCiC; R2KRi/{K-l); Rs=KR,.

36. Если К=1, использовать схему, изображенную на рис. 3.15,6, и значение сопротивления Ru как определено в п. За.

4. Звенья второго порядка этого фильтра нечетного порядка можно реализовать, как указано в § 3.8-3.10 и сформировать фильтр, соединив их каскадно с звеном первого порядка.

Комментарии

Эти комментарии идентичны с комментариями, изложенными в § 2.13 по расчету звена фильтра нижних частот первого порядка.

ГЛАВА ЧЕТВЕРТАЯ ФИЛЬТРЫ ВЕРХНИХ ЧАСТОТ

4.1. ОБЩИЙ СЛУЧАИ

Фильтр верхних частот представляет собой устройство, пропускающее сигналы высоких частот и подавляющее сигналы низких частот. На рис. 4.1 изображены ;идеальиая и реальная амплитудно-частотные характеристики, где для практического случая обозначены полоса пропускания (0>Шс, полоса задерживания O:co<ui, переходная область coi<co<«c и частота среза Шс (рад/с), или fc=4>cl2n (Гц).

Передаточную функцию фильтра верхних частот с частотой среза Шс можно но-.лучить из передаточной функции нормированного фильтра нижних частот (имеющего СОс, равную 1 рад/с) с помощью замены неременной s на coc/s [32]. Следовательно, функция фильтров верхних частот Баттерворта и Чебышева будет со-.держать следующие сомножители второго порядка:

где СОс - частота среза, а В и С представляют собой приведенные в приложении А нормированные коэффициенты звена -фильтра нижних частот второго порядка. При нечетном порядке присутствует также звено первого порядка, обладающее передаточной функцией вида

Н = -гг=

(4.2)

где С - нормированный коэффициент нижних частот первого порядка.

Фильтр верхних частот Баттерворта имеет монотонную характеристику, подобную-характеристике на рис. 4.1, тогда как характеристика фильтра верхних частот Чебышева характеризуется пульсациями в полосе пропускания. Например, фильтр верхних частот Чебышева с неравномерностью передачи 1 дБ, подобно его прототипу нижних частот, имеет пульсации 1 дБ в диапазоне полосы пропускания. Для иллюстрации этого случая на рис. 4.2 приведена характеристика реального фильтра верхних частот Чебышева седьмого порядка с неравномерностью передачи 0,5 дБ.

Коэффициент усиления фильтра верхних частот представляет собой значение его передаточной функции при бесконечном

\H(Jw)\

Идеальная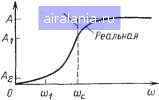

Рис. 4.1. Идеальная и реальная амплитудно-частотные характеристики фильтра верхних частот.

Рис. 4.2. Амплитудно-частотная характеристика реального фильтра Чебышева верхних частот.

значении переменной s. Следовательно, для звеньев второго и первого порядков, описываемых соответственно уравнениями (4.1) и (4.2), коэффициент усиления звеиа равен К-

Инверсные Чебышева и эллиптические фильтры состоят из звеньев второго порядка с передаточными функциями следующего вида:

-s=+(Bco/C)s + coVC

(4.3)

где Л, В и С - нормированные коэффициенты нижних частот из приложения Б или В. В передаточные функции фильтров нечетного порядка входит звено первого порядка с передаточной функцией

(4.4)

где С - коэффициент звеиа первого порядка нижних частот из приложения Б или В. В обоих уравнениях (4.3) и (4.4) К является коэффициентом усиления звена.

Как для фильтра верхних частот Баттерворта или Чебышева второго порядка (4.1), так и для инверсного Чебышева и эллиптического фильтров (4.3) добротность Q, аналогично фильтру нижних частот, определяется соотношением Q-Vc В.

Амплитудно-частотная характеристика инверсного фильтра Чебышева верхних частот монотонна в полосе пропускания и обладает пульсациями в полосе задерживания, значение которых характеризуется минимальным затуханием в полосе задерживания (MSL) в децибелах. В каждом случае частота Юс выбирается по уровню затухания 3 дБ. Амплитудно-частотная характеристика эллиптического фильтра верхних частот содержит пульсации в полосах пропускания и задерживания и характеризуется соответственно неравномерностью передачи в полосе пропускания (PRW) и минимальным затуханием в полосе задерживания (MSL) в децибелах.

Ширина переходной области TWgq фильтра верхних частот связана с нормированной шириной переходной области TW его прототипа нижних частот следующим соотношением (рад/с)

или (Гц)

(4.6)

Например, эллиптический фильтр верхних частот второго порядка с PRW=0,5 дБ и MSL=60 дБ имеет в нормированном прототипе нижних частот значение TW=0,4014 (из приложения Г). Следовательно, если частота /с=1000 Гц, ширина его переходной области определяется из (4.6):

0,4014

"64 = 1:40°°° = Гц.

Наоборот, можно найти TW по заданному значению TWgjj из (4.5) или (4.6) и в-

результате получим

TW=1/[(ioc/TWb4)-1]. (4.7).

Минимальный порядок фильтра верхних частот, ширина переходной области которого не превышает TWgq, следовательно, такой же, как и порядок нормированного фильтра нижних частот с шириной переходной области, не превышающей TW. Например, если необходимо получить минимальный порядок эллиптического фильтра верхних частот с fc=1000 Гц, PRW=0,5дБ, MSL=6p дБ и с TWgij, не превышающей 100 Гц, то из (4.7) получаем

TW=1/(1000/100-1)=0,1]]1.

Следовательно, для нормированного-случая нижних частот ширина переходной области не должна превышать 0,1111. Из приложения Г находим, что минимальный порядок п=9.

4.2. ФИЛЬТРЫ ВЕРХНИХ ЧАСТОТ С МНОГОПЕТЛЕВОИ ОБРАТНОЙ

СВЯЗЬЮ И БЕСКОНЕЧНЫМ КОЭФФИЦИЕНТОМ УСИЛЕНИЯ

Фильтр верхних частот Баттерворта; или Чебышева второго порядка, так же как. и его прототип нижних частот, можно реализовать на схеме с многопетлевой обратной связью (МОС) и бесконечным коэффициентом усиления, схеме на ИНУН и-биквадратной схеме. В этом параграфе будет исследована схема с МОС [9], а два других типа рассматриваются в следующих параграфах.

Фильтр с МОС, показанный на рис. 4.3, реализует функцию верхних частот второго порядка типа (4.1) с инвертирующим коэф-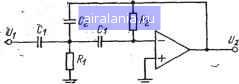

Рис. 4.3. Схема фильтра верхних частот с МОС и бесконечным коэффициентом усиления.

<фициентом усиления - К(К>0) при

(4.8)

Bto/C = (2С,-f C,)/i?AC2;

mVC=1/i/?2CA- •

Решение относительно знэчений элементов имеет вид:

/, = £/(2С, + С2)со,; (4.9)

/?, = (2С, + С2)С/ВСАйс.

-где Cl имеет произвольное значение. Следовательно, можно выбрать значение емкости

Cl (предпочтительно близкое к значению 10/fc мкФ) и определить значения емкости и сопротивлений. Если 1/К представля-

>ет собой номинальное значение емкости, допустим, 1,2 или 1/2, то Сг также будет

-иметь номинальные значения: Ci, 2Ci или

Что касается достоинств фильтра верхних частот с мое, то они такие же, как у его прототипа фильтра нижних частот, описанного в i§ 2,5. Краткое изложение методики расчета приведено в § 4.8.

4.3. ФИЛЬТРЫ ВЕРХНИХ ЧАСТОТ НА ИНУН

Схема на ИНУН, реализующая функцию фильтра верхних частот Баттерворта

или Чебышева второго порядка вида (4.1), изображена иа рис. 4.4 [26]. Анализируя эту

схему, получаем

Выг 1 „. 2 I

(1-К) +

(4.10)

С RC,

o>cVC= l/R,R,JC,.

Коэффициент усиления схемы - неин-вертиругощий, а значения сопротивлений определяются следующим образом:

[В + Ув-\-8С{К-1)1 соС, .J?, = C/VC,=R2; .Rs = KR/(K-\); R = KR2,

.тде Cl имеет произвольное значение.

(4.11)

Щ Cl -1Ь-

Рис. 4.4. Схема фильтра верхних частот на ИНУН.

Если К=1, то в качестве сопротивления йз можно взять разомкнутую, а сопротивления Ri - короткозамкнутую цепь и в этом случае ОУ работает как повторитель напряжения, а сопротивления Ri и Rz не изменяются.

Преимущества схемы верхних частот иа ИНУН такие же, как у схемы нижних частот на ИНУН, рассмотренной в § 2.6. Краткое изложение методики расчета приведено в § 4.9.

4.4. БИКВАДРАТНЫЕ ФИЛЬТРЫ ВЕРХНИХ ЧАСТОТ

Биквадратная схема второго порядка, реализующая фильтр верхних частот Баттерворта или Чебышева с инвертирующим коэффициентом усиления, изображена на рис. 4.5 [8]. Анализ этой схемы дает

К = RJR\ Bwc, С = l/RjCi; oЛC=l ?з?5C,

(4.14)

RtR.RR. (4.13)

Значения сопротивлений определяются следующими соотношениями:

/?, = С/В/СюС,; = KR; R, = C/C,c,R,; R = R,/K

где С] и /?5 имеют произвольные значения.

Как и для фильтра нижних частот, биквадратная схема фильтра верхних частот содержит большее число элементов, чем фильтры с МОС и на ИНУН. Однако этот недостаток компенсируется большими воз-

.,Ci

-rt>

Рис. 4.5. Схема биквадратного фильтра

верхних частот. j