Or

/ /л

V / /

На О-

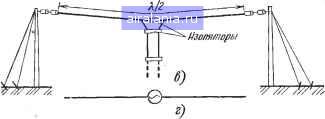Рис. 3.5. Вертикальная заземленная антенна (а) и ее электрическая схема (б); симметричный горизонтальный вибратор - диполь (е) и его электрическая схема (е); условное обозначение проволочной антенны (д) и ее эквивалентная

схема (е)

. Рассмотрим вопрос о технических показателях работы антенн. Антенна как радиотехническое устройство характеризуется рядом электрических (радиотехнических) параметров. Следует отметить, что некоторые из параметров, такие как характер распределения излучаемых электромагнитных волн в пространстве, их поляризация, коэффициент полезного действия и др., относятся к антеннам любого типа. Такие же параметры, как входное сопротивление (в омах) или так называемая действующая высота, являются характерными для проволочных антенн.

Одна и та же антенна, не содержащая нелинейных элементов, может служить для радиопередачи и для радиоприема и в силу известной в теории антенн теоремы взаимности обладает свойствами обратимости. Параметры антенны в режиме передачи обычно характеризуют также антенну и при использований ее для приема, при этом некоторые из параметров несколько изменяют свой смысл.

Основным параметром антенны как нагрузки для генератора или фидера является ее входное сопротивление.

Входное сопротивление антенны, питаемой проводной линией, определяется отношением напряжения высокой частоты f/a на зажимах антенны к току питания /а (рис. 3.5,е):

2а = f/a a-

(3.3)

Антенна

Передатчик

в общем случае это сопротивление зависит от частоты и содержит как активную Ra, так и реактивную составляющие, так что модуль полного сопротивления

Zal=l/"!T3cf. (3.4)

Сопротивление излучения и коэффициент полезного действия антенн. Под

водимая к антенне мощность Ра частично излучается, а частично расходуется бесполезно в активном сопротивлении проводов антенны, в земле, в окружающих антенну проводниках и других предметах (оттяжках, строениях и т. д.).

Излучаемая антенной мощность Pj. пропорциональна квадрату действующего значения тока в антенне h:

P = fil (3-5)

где - коэффициент пропорциональности, который измеряется в омах и называется сопротивлением излучения антенны, отнесенным к току /а.

Таким образом, сопротивлением излучения антенны Rj. называется сопротивление, в котором могло бы теряться столько же энергии, сколько излучается антенной в пространство. При определении сопротивления излучения следует оговаривать, к какой точке антенны оно относится, так как сила тока в разных точках вдоль антенны различна. Сопротивление излучения зависит от формы антенны, ее геометрических размеров и от длины волны, на которой работает антенна.

Понятие (и термин) «сопротивление излучения антенн» было введено М. В. Шулейкиным. Используя выражение для мощности излучения, полученное Герцем для элементарного электрического диполя, М. В. Шулейкин вывел формулу для сопротивления излучения (в омах) такого диполя, которая имеет вид

Л£ = 80я2( Я)2~800(/Д)г. (3.6)

Здесь l/X - отношение длины диполя к длине волны. Из полученной формулы видно, что сопротивление излучения проволочной антенны получается не очень малым лишь для размеров, соизмеримых с длиной волны.

Следует подчеркнуть, что по формуле (3.6) сопротивление можно рассчитать лишь при условии (как для диполя Герца), что ток вдоль антенны не меняется по амплитуде. Если это условие не выполняется, в формуле (3.6) длину I надо заменить действующей длиной антенны (понятие о ней дается ниже).

Излучаемая антенной мощность является полезной мощностью, и соответственно сопротивление излучения является полезным активным сопротивлением антенны, в отличие от другой части активного сопротивления антенны, обусловливающего потери.

Мощность потерь в антенне, так же как и мощность излучения, пропорциональна квадрату тока в антенне. Поэтому можно записать, что мощность потерь

PnllRn. (3-7)

где - эквивалентное сопротивление потерь, отнесенное к току /а в точках

питания антенны. Сумма мощности излучения Pj, и мощности потерь Рп дает полную мощность в антенне:

Pa=P2 + Pn = /a(2: + n)=/f?a. (3.8)

где Rs,=R-i-Ra - полное активное сопротивление антенны. Для оценки эффективности работы антенны вводят понятие коэффициента полезного действия антенны, под которым понимают отношение излучаемой мощности к полной мощности антенны:

Г]=-

(3.9)

Из последнего выражения видно, что для увеличения КПД антенны надо по возможности уменьшать Рп по сравнению с Rj..

HanpaBjieHHoe действие антенн. В некоторых случаях необходимо, чтобы антенна передающей радиостанции одинаково интенсивно излучала во всех направлениях. Например, при работе радиовещательной станции, обслуживающей определенный район, в центре которого она расположена. Но иногда, например, когда передатчик должен обслужить радиоприемник, расположенный в определенном направлении, а также при работе радиолокационных установок необходимо концентрировать электромагнитную энергию в определенных направлениях. В таких случаях целесообразно применять антенны направленного действия, отличающиеся способностью концентрировать излучение в заданных направлениях.

Наглядное представление о распределении энергии волн дает амплитудная характеристика направленности, определяемая зависимостью амплитуды напряженности создаваемого антенной поля (или величины, ей пропорциональной) от направления в пространстве. Направление определяется азимутальным ф и мерндиальным 6 углами сферической системы координат, как показано на рис. 3.6. При этом поле определяется на одном и том же (достаточно большом) расстоянии г от антенны и предполагается, что потери в среде отсут-втвуют. Графическое изображение характеристики направленности называют диаграммой направленности (ДН).

Пространственная диаграмма направленности изображается в виде поверхности /(ф, 6), где / - знак функциональной зависимости. Построение такой

диаграммы неудобно. Поэтому на

Меридиональный угол

Азимутальный I угол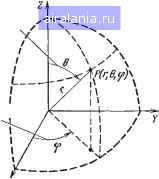

практике обычно строят диаграмму направленности в какой-нибудь одной плоскости, в которой она изображается плоской кривой /(ф) или или /(6) в полярной или декартовой системе координат.

Данное определение относится к диаграмме направленности по полю. В некоторых случаях используется понятие характеристики (диаграммы)

Рис. 3.6. Сферические координаты точки наблюдения