Применение ЭВМ

МЕТОДЫ РАСЧЕТА СРЕДНИХ ТЕМПЕРАТУР

ПО МОДЕЛЯМ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ

§ 1.1. СИСТЕМЫ УРАВНЕНИЙ ТЕПЛОВОГО БАЛАНСА

Наиболее полные математические модели процессов теплообмена протекающих в различных технических устройствах, учитывают наличие неравномерных пространственно-временных полей у искомых величин - температур твердых тел и жидкостей, тепловых потоков, интенсивностей излучения и т. д. Такие модели представляют собой системы дифференциальных уравнений в частных производных, интегральных и интегродифференциальных уравнений. Однако при решении реальных технических задач, как правило, не ограничиваются использованием только таких моделей, что объясняется несколькими причинами.

Во-первых, для многих технических устройств непосредственная реатизация полных математических моделей затруднительна даже с применением современных ЭВМ из-за сложной структуры устройств и большого числа входящих в них элементов. Возникающие трудности связаны как с проблемой выбора метода решения и требуемыми объемами машинного времени и памяти, так и с объемом исходной информации, входящей в полную модель. Для анализа теплоюго режима таких систем применяется метод поэтапного моделирования [5], предполагающий последовательное использование более простых, по сравнению с полной, моделей, описывающих всю систему и отдельные ее части с разной степенью детализации.

Во-вторых, основным методом проектирования сложных систем является блочно-иерархический [17], при котором в процессе проектирования система рассматривается последовательно на разных уровнях иерархии с постепенно нарастающей степенью детализации. При этом анализ процессов теплообмена на каком-либо высшем уровне нужно проводить в условиях, когда внутренняя структура подсистем этого уровня еще детально не определена, и поэтому полную .модель нельзя использовать из-за недостатка информации.

Наконец, решение многих технических задач просто не требует знания детальной информации о пространственных распределениях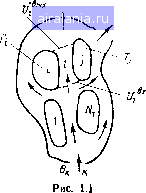

искомых величин, что позволяет ввести упрощения в полную модель и ответить иа интересующие вопросы более быстрым и дешевым путем.

Все это делает весьма актуальным рассмотрение упрощенных моделей, позволяющих рассчитывать интегральные характеристики процессов теплообмена и описываемых системами алгебраических иобыкновенных дифференциальных уравнений. В дальнейшем такие модели будем называть моделями с сосредоточенными параметрами, отделяя их тем самым от моделей с распределенными параметрами, которые учитывают пространственные распределения физических величин.

Практика показывает, что при реализации моделей с сосредоточепны.ми параметрами целесообразно выделять достаточно общие модели этого вида и разрабатывать для каждой из них универсальное программное обеспечение, позволяющее решать широкий круг конкретных задач. В данном разделе рассмотрим методы численного расчета и программную реализацию для одной из таких моделей, которая позватяет проводить расчет средних температур в системе тел и потоков теплоносителей, находящихся во взаимном теплообмене. Описываемые ниже методики и приемы типичны и для других моделей с сосредоточенными параметрами.

Перейдем к описанию модели для расчета средних температур. В этой модели рассматриваются объекты трех видов: Лт объемов - твердых тел с равномерными температурными полями (т), в которых действуют источники теплоты с мощностями Я,-; Nобъемов - каналов с протекающими в них теплоносителями, имеющими средне-объемные температуры Ui{x) и сред немассовые температуры на входе и выходе каналов Ui (т) и бТ" (f); Лс объемов - сред с постоянными температурами (рис. 1.1).

Твердые тела находятся в теплообмене друг с другом, а также с теплоносителями и со средами. В данной модели предполагается, что тепловые потоки, приходящие к данному телу i от соседних тел {Р]}), а также от теплоносителей (ЯГ) и от сред {Р]1), можно выразить через разности их средних температур в виде

P]]ojj{Tj~Tiy, P]f = fiUi~Tt), P]l=°]l(-i)

где aJJ, aJJ, a]l - тепловые проводимости между телами i и /, телом i и теплоносителем /, телом ( и средой k соответственно. Тепловые проводимости рассчитывают на основе соответствующих коэффициентов теплоотдачи и размеров [5, 12. 31]. Они могут учитывать различные механизмы переноса теплоты.

Поскольку МОЩНОСТЬ Pi, выделяющаяся в теле расходуется на его нагрев и передается окружающим телам, теплоносителям и средам, уравнение теплового баланса для него записывается в виде

4.2)

где С} - полные теплоемкости тел.

Тепловой поток, поступивший от тел к теплоносителю в объеме /, расходуется на его нагрев в этом объеме, а также выносится из объема вытекающим потоком теплоносителя. Поэтому уравнение теплового баланса для теплоносителя имеет вид

а-(Г,-= Cf + c,Gr(VTVri (1.3)

гдеСГ

полная теплоемкость теплоносителя в объеме /; ci - удельная теплоемкость; G; - массовый расход теплоносителя, протекающего через объем /.

В модели допускается, что на входе в /-й канал можег происходить смешение нескольких потоков, одни нз которых вытекают из других каналов (индекс т), а другие - из объемов (индекс k), имеющих известные температуры 6. Тогда для среднерасходной температуры теплоносителя на входе в /-й канал Uf" справедливо соотношение

2 o„]vf ft -1 /

т = I

г 7ВЫХ

ml L-rti

ft = 1

hi Oft,

(1.4)

\ m = I

где G,t,i, - массовые расходы теплоносителей, втекающих в /-й канал из m-ro канала и /г-й среды с постоянной температурой соответственно.

Для замыкания системы уравнений {1.2)-(1.4) необходимо иметь соотношение, связывающее среднюю температуру L/j с температурами VY, t/f". Это соотношение можно получить на основе того или иного допущения о -чарактере пространственного изменения температуры теплоносителя. Например, при линейном изменении температуры подлине канала справедливо равенство V [ = {VY + и])!2\ При интенсивном перемешивании теплоносителя в объеме VI = f/". Обобщением этих соотношений является выражение

которое и будет использоваться в дальнейшем.

Подставив выражение (1.5) для Ui и выражение для иГ из (1.4) в уравнения (1.2), (1.3), получим систему (Nr + /V ж) уравнений от-носительно неизвестных температур /;(: = !, 1т) и (* =

1.....Л"). Для полной постановки задачи задаются значения искомых температур в начальный момент времени

It---о - TiQ,

(1.6)

Таким образом, задача определения нестационарных средних температур твердых тел и теплоносителей сводится к решению системы обыкновенных дифференциальных уравнений при заданных в начальный момент времени значениях неизвестных функций Ti (т), t/f"" (т). т. е. к решению задачи Коши 2).

В случае, когда температуры постоянны во времени, производные по времени следует приравнять нулю, и в результате получается система алгебраических уравнений относительно искомых температур.

Тепловьсе проводимости, теплоемкости и мощности могут зависеть от искомых температур. Поэтому в общем случае получающиеся системы уравнений являются нелинейными. Однако при решении систем нелинейных уравнений обычно организуют итерационный процесс, при котором определение очередного приближения проводится путем решения системы линейных уравнений, в которой проводимости, теплоемкости и мощности рассчитаны по значениям температур, найденным иа предыдущей итерации. Решение систем линейных алгебраических уравнений лежит также в основе некоторых методов решения систем обыкновенных дифференциальных уравнений-

Изложение методов решения систем алгебраических уравнений, начнем с линейных систем.

§ 1. МЕТОДЫ РЕШЕНИЯ СИСТЕМ АЛГЕБРАИЧЕСКИХ УРАВНЕНИИ

Рассмотрим методы решения системы N линейных алгебраичее-fux уравнений вида

которую будем записывать далее в сокращенном виде

V OijUjbi, 1 = 1.....N,

(1.7)

(1.8) 9

или в матричной форме

Q21 О22

AU-B,

/"1 \

\bN/

(1.9) (1.10)

где A - квадратная матрица размером N X N; В - вектор-стол-: бец правых частей; U - вектор-столбец неизвестных с Л компоиен-у, тами.

Методы решения систем линейных алгебраических уравнений разделяют на две группы: прямые и итерационные. В прямых методах решение находят за конечное число действий, зависящее от числа неизвестных jV, и это решение было бы точным, если бы при выполнении арифметических операций не было погрешностей округления, т. е. если бы действия проводились с неограниченным числом знаков.

В итерационных методах сначала задается некоторое начальное приближение к решению а затем реализуется повторяю-

щийся процесс определения последовательных приближений {"nInP в котором каждое s-e приближение находится на основе предыдущего (s - ])-го {"*~При возрастании номера итерации S приближенное решение стремится к точному. Итерационные методы применяют для решения не только линейных, но и нелинейных систем алгебраических уравнений.

Выбор метода решения иа ЭВМ системы линейных алгебраических уравнений зависит от свойств матрицы А, числа уравнений Л и возможностей ЭВМ - объема оперативной памяти, быстродействия и числа значащих цифр, с которыми ведутся вычисления. В настоящее время в прикладном программном обеспечении ЕС и СМ ЭВМ имеется достаточно большое число программ, реализующих прямые методы. Здесь мы рассмотрим только одни прямой метод - метод Гаусса. Некоторые другие прямые методы - метод прогонки, метод квадратного корня - будут рассмотрены ниже в главах 3 и 4 при обсуждении алгоритмов решения тех задач, где их использование наиболее эффективно.

Метод последовательного исключения Гаусса. Этот метод основан на простой процедуре, которой многие интуитивно пользуются при «ручном» решении систем. Это последовательное исключение неизвестных «1, «iv-i и получение в конечном итоге уравнения с од- ним неизвестным и. Одновременно осуществляется преобразование уравнений системы, которое позволяет после определения пооче- редно найти остальные неизвестные в обратной последовательности:

прпвом шаге алгоритма исключают неизвестное и, из уравне-" . ипмепами 2 3, N. Чтобы исключить из к-го уравнения, поступают так: первое уравнение умножают на aja,, н вычитают из kTO уравнения:

у ajUj-(аг/ап) % ау щ==ЬаМау .

В результате получают преобразованное k-e уравнение, в котором присутствуют неизвестные и.,, "з. . и отсутствует неизвестное

V a\iU.==bl, al, = a„j-ak,aijlai, (1.11)

bk- b - Qkibjaji,

Здесь верхний индекс «I» означает, что выполнен первый шаг исключения.

Повторяя такую процедуру для уравнений с номерами 2, после окончания первого шага получают следующую систему:

022 Н----"Ь 2iV = b\.

(1.12)

Отметим, что первое уравнение осталось неизменным и оно (т. е. его коэффициенты) «оставляется на хранение» в машинной памяти.

Далее приступают ко второму шагу алгоритма, на котором ча уравнений системы (1.12) с номерами 3, jV аналогичным образом исключают неизвестное Ыа и получают систему с преобразованными по сравнению с (1.12) последними (Л - 2) уравнениями вида

ah "з + --- + UNbl, (I-13)

033 "a + ... +аз u

cthiij-l- ...-\-a%N uj=b%,

alf-----al/ - al2a2)/ah-2, blbi - al?blla2. (1-Й)

К уже хранящимся коэффициентам первого уравнения системы (1-12) добавляются коэффициенты второго уравнения системы (1.13).