ции ф/. Это обстоятельство можно качественно нстоткова благоприяТ11ый исход «борьбы» между уменьшением painJ " "е-н разностных уравнений (невязок,/) и увеличением

у-

разностных уравнений (невязок.ф/) и увеличением общего уравнений (при Лт О, /i- О число узлов сеткн NJ оо) - тнм, что в реальных задачах заметная раскачка схемы может яаст пить после нескольких десятков нлн даже нескольких еднниц ща-;

Для устойчивых схем такого роста погрешности не происходи! Величина е> остается ограниченной и уменьшается при уменьшенян погрешности аппроксимации ф, несмотря на то, что при нзмельчеицц

пространственно-временной сеткк увеличивается число решаемых уравнений (число узлов NJ). Таким образом, условие устойчивости можно записать как условие выполнения неравенства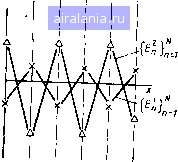

(3.21)

прн Достаточно малых h н Дт н постоянной В, независящей от h н x Прн более оби1ей математической трактовке устойчивость рас-сматривается как свойство разностной схемы. Которое заключается в том, что малым изменением правых частей в системе алгебраических уравнений разностной схемы соответствуют малые изменения разностного решения.

Еслн условие (3.21) РыПолняетсй прн любом соотношении между шагами Дт и Л. to схему называют безусловно устойчивой. Еслн устой чивоСть имеет место лишь при условии выполнения определенного соотноШ&нйя между шагами по Пространственной координате и по Времени* то схёМу называют условно уаПойчивдй.

Математический анализ устойчивости разнОСтйых схем ЧлстО представляет собой достаточно сложную задачу, методы решения ко торой рассматриваются в книгах 14,14. 24, 25]. В данном кур* будем Приводить peзyЛbfatы Исследовэиня yctoft4HBOtTH различных XeU без их дЬказательств.

Как уже было отмечено выше, на практике отсутствие устойчивости легко устанавливается экспериментальным путем прн появ1б= ннй «разболтки» численного решеййЯ в процессе пробных раСчетОВ.

Теперь рассмотрим связь между аппроксимацией, устойчиво Стью н СХОДИМОСТЬЮ: при наличии аппроксимации [условия (3.20)1 н устойчивости [условия (3:21)] всегда имеет место и сходимость. Действительно, из условия аппрокснмйции

условия устойчивости

тогдз

u-t-*o. ft-0

= limlri-

пазностное решение сходится к точному, причем порядок точ-схемы совпадает с порядком аппроксимации.

ЯВНАЯ И НЕЯВНАЯ СХЕМЫ

Д7Я решения нестационарных одномерных задач теплопроводности можно построить большое число «разумных» разностных схем. Однако мы рассмотрим только те разностные схемы, важность которых подтверждена вычислительной практикой.

В связи с наличием в иестационарном уравнении теплопроводности двух дифференциальных операторов -- по временной и пространственной переменным - различают два вида схем: явные и неявные. Рассмотрим особенгюсти этих схем на примере решения одномерной нестационарной задачи (3.1) -(3.3) на равномерных пространственной и временной сетках (см. рис. 3.1).

Разностную схему для определения разностного решения будем по-прежнему строить, заменяя в уравнении (3.1) и граничных усло-внял (3.2), (3.3) производные конечными разностями. Рассмотрим аппрокснмаиню производной по времени. В принципе для построения соотношений, аппроксимирующих временную производную, в /й момент времени можно использовать значения температур в различные моменты времени: Tj, 7"". 7"" ... . Однако на практике в подавляющем большинстве случаев используются только значения температуры в /-й и (/ - 1)-й моменты времени. Такие схемы называются двухслойными ((Ю времени). Значительно реже учитывают значение температуры в (/ -2)-й момент времени н получают Трехслойные схемы. Дальше мы будем рассматривать только двухслойные схемы. В этом случае производную по времени аппроксимируют разностью назад

дх 4т

При двухслойной схеме пространственный дифференциальный Оператор целесообразно аппроксимировать также на основе значений температуры в /-й и (/ - ])-й моменты времени. При этом Нанболь-Щее распространение получили два «крайних» случая. В первом "Тучае при аппроксимации используются только значения температуры для искомого, «настоящего» /-го момента времени:

дх"-

(способ аппроксимации второй производной dTIdx был рассмотри § 3.1), а во втором - только значения температуры для «прощ го», предыдущего момента времени (/ - )):

Соответстоеииополучают два различных разностных уравнен,,, аппроксимирующих уравнение теплопроводности (3-i):

-2ui

,/-1

(3.22,

(3.23}

Для аппрокси.мации граничных vcioru /-iП омся простейшим снособом\замень производных ппГ ""У" вои и левой разностями. СоответственГполучаем ™P««3e пра-

и, - и

1г---1- о«/"-о,

(3.241 (3.25)

зо,м

Начальное условие для раяностной схемы задается точным обра-

(3.26)

В $ 3.1 мы уже доказали, что записанные разностные уравнения аппроксимируют уравнение теплопроводности с порядком О (Дт + -К) и граничные условия с порядком О (h). Уравнения (3.22) или (3.23) вместе с уравнениями (3.24) - - (3-26) образуют разностные схемы, позволяющие найти сеточную функцию иЛ Рассмотрим, в чем заключается принципиальная раз-ница между схемами, использующими уравнения (3.22) и (3.23).

Начнем со схемы (3,23) - (3.26). Уравнение (3.23) позволяет выразить в явном виде неизвестное значение ui сеточной функции на «новом» временном слое / через известные значения сеточной функции на предыдущем {/ - 1)-м слое:

п1, -«Ат{ г!--2»; -Ч "1) 1-Ь.Лт/грН- иГ. (3.27f Так как в начальный момент времени значения и\ заданы условием (3.26), то ио формуле (3.27) можно найти сначала а\ для внутренних узлов п 2, .... N - \, а затем из граничных уравнении (3.24), (3,25) о((ределить uf и а\>. Аналогичная процедура проводит-ся для отыскания сеточной функции па втором временном слое и т. Д-

разностная схема (3.23)~(3.26) называется явной, так как поз-j,fleT искомые значения сеточной функции и/ б явном, виде выразить через найденные ранее значения и-. Алгоритм численного расчета по явной схеме очень прост и легко программируется. Перейдем к разностной схеме, заданной уравнениями (3.22), (3.24)-(3,26). Здесь ситуация сложнее, поскольку в каждое уравнение вида (3.22) кроме неизвестного значения и/, для п-й пространственной точки входят еще два искомых значения сеточной функции "„1 Ачя соседних {п - 1)-й и {п + 1)-й точек. Поэтому рас-

/, . и

смотренный выше для явной схемы прием получения явной формулы для неизвестного значения в этой ситуации не проходит. Все искомые значения {uJ оказываются «завязанными» друг с другом в общую нераспадающуюся систему уравнений. Эта система состоит из (Л/ - 2) уравнений (3.22) для внутре1ших узлов и двух уравнений (3.24), (3.25), соответствующих граничным условиям. Всего имеем N уравнений относительно Л неизвестных Таким об-

ра.зом, в данном случае на каждом временном слое значения сеточной функции ип определяются не по явным формулам, а из решения системы N уравнений, поэтому рассмотренная разностная схема называется неявной. Эффективный алгоритм решения системы уравнений (3.22), (3,24), (3.25) рассмотрим ниже.

На первый взгляд явная схема предпочтительнее, так как она имеет такой же порядок аппроксимации О (Дт + h), как и неявная, но не требует решения на каждом шаге по времени систем N уравнений. Однако более подробный анализ показывает, что явная схема условно устойчивая, т. е. устойчивая при определенном ограничении на величину шага по времени Дт. Условие устойчивости для явной схемы (3.23) - (3.25) имеет вид

Ат Дту,,-/12а. (3.28)

Из условия устойчивости следует, что измельчение пространственной сетки должно сопровождаться измельчением временной сет-и. Например, при увеличении числа пространственных узлов Д в рзза, требуется увеличить число шагов повремени в 16 раз. Необ-одимость соблюдения условия (3.28) приводит к тому, что при определении шага повремени для решения реальной нестационарной задачи мы не можем исходить только из характера протекания во вре-"ни изучаемого физического процесса. Это в ряде случаев приво-Д*т к неприемлемым затратам машинного времени. Кроме того, при Неоправданно больпюм числе временных шагов может начать проявляться погрешность округления, возникающая в ЭВМ при реа--изации арифметических операций.

Неявная схема (3.22) безусловно устойчивая, т. е. явление не-Утойчивости не возникает при любых величинах Дт. Поэтому при

НИИ задачи по неявной схеме величину шага по времени задают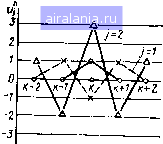

только из соображений обесп требуемой погрешности решения.

Проиллюстрируем «физический м хаиизм» возникновения неустойчив сти при расчете по явной схеме примере плоской стенки без нсточц. ков теплоты. Положим, что нача;[ь ная температура стеики равна HyitQ во всех точках простраиственно}! сетки, кроме одной точки с номером п = k (рис. 3.4); и« = О, п -. 1, /V, п 7 fe; и% 1. Пусть h \, а = 1. Выберем 4т = 1, т. е. величина шага вдвое превышает условие устойчивости (3,28). Расчет по явной схеме ведется по формуле (3.27), которая в данном случае записывается в виде:

Рис. 3.4

Выполняя расчет, получим следующие данные:

Из рис. 3.4 видно, что возникает «разболтка» и получается разностное решение с возрастающими по величине от слоя к слою значениями не имеющее ничего общего с точным решением, представляющим функцию, которая принимает только положительные значения и убывает в точке с номером к. «Разболтка» началась из-за того, что температура и\ «упала» в отрицательную область и стала меньше, чем температуры соседних точек, что противоречит физическому смыслу. Нетрудно убедиться, что при расчете иа границе устойчивости с шагом 4т = 0,5 получим ul = 0,5, til О, Um~i ~ 0,5, т. е. все температуры положительны и не превышают температур соответствующих им соседних точек на предыдущем временном слое. Дальнейший расчет с шагом 4т = 0,5 привел бы к получению колеблющегося решения с убывающей нормой

Расчет же по неявной схеме при любом 4т дает решение, правильно отражающее качественный характер изменения температУ" ры.

Рассмотренному отличию в поведении решений, полученных по явной и неявной схемам, можно дать следующее физическое объяс-

1,ри расчете по явной и неявной схемам предполагается, что шя меняется линейно на интервале hj-i, Т;1, но значение фУ" рдиой по времени при явной схеме вычисляется по значениям мой функции в начале временного интервала, поэтому прираще-искомой функции (и! - ") зависит от получаемых зна.. "ий а абсолютная величина этого приращения пропорциональна см. (3.27). В результате при некотором критическом шаге 4т можем получить новые значения и, противоречащие физиче-"пмУ смыслу задачи, как это и было в рассмотренном примере.

неявной же схеме приращение {uj - W) зависит от всех значений ИОВОМ временном слое, т. е. имеется как бы йобозтиая связь», не позволяющая получать абсурдные приращения сеточной функции. Например, при решении задачи нагрева тела внутренними источниками теплоты по неявной схеме при любом Ат тюлучается решение с температурами, ие превышающими стационарные значения.

Можно построить разностную схему, являющуюся линейной комбинацией явной и неявной схем с весовыми коэффициентами с и

(1-<):

(3.29)

Эту схему называют схемой с весами. Видно, что схема (3.29) при о Ф О неявная, так как содержит в правой части искомые значения uj, ",tli Иовом временном слое. Чтобы отличить неявную схему (3.22), последнюю называют чисто неявной.

Схема с весами безусловно устойчива при а 1/2, а прн а <1 < 1/2 условие устойчивости имеет вид

4r<AV[2d(l-2о)Ь (3.30)

Кроме предельных случаев явной (о = 0) н чисто неявной (сг=1) схём достаточно часто применяют схему с весом сг = 1/2, иазывае-Myfc схемой Края-ка Никйлсона, Эта схема имеет более высо *йя (второй) порядок аппроксимации по времени; Hvi I =

О (Дт -f а также Является безусловно устойчивой. Однако схёма Кранка - Николсоиа имеет недостаток, который мы обсудим далее; в коНцё § 3.3.

В заключение отметим, что обычно в книгах после проведения Сопоставления явной и неивной схем, подобного рассмотренному biUie, делается вывод о нецелесообразности применений явных Хем. Однако практика решения реальных задач не подтверждает безусловную правильность такой рекомендации. В пользу явной