виду, что иа - ЭТО некотороб приближение к искомому зна ип. Таким образом, разностная схема (3.67) принимает вид

(3.70)

где номер итерации s принимает значения 2, т. е. урав

нения (3.70) решаются на каждом шаге по времени k раз, Уравнр ния для граничных точек преобразуются аналогично.

В качестве нулевого приближения uf* берутся значения температур с предыдущего вре.менпого слоя, т. е. и] t--- и{г\ Далее k раз решают уравнеиия разностной схе.мы вида (3.70) и определяют значения температур иа новом временном слое: ип - иЦК Число итераций k либо фиксируется (обычно задают к = 2~f 4), либо определяется из условия получения заданной пограпиости решения системы нелинейных разностных уравнений на текущем шаге. В последнем случае итерации прекращают при выполнении условия

В такой схеме объем вычислений возрастает по сравнению с квазилинейной схемой, так как иа каждом шаге по времени приходится решать методом прогонки систему разностных уравнений не один, а к раз. Однако нелинейная схема дает меньшую погрешность численного решения исходной задачи (3.64) - (3.66), чем квазилинейная. Это объясняется тем, что коэффициенты в выражениях для сеточных аналогов тепловых потоков вычисляются в тот же момент времени, что и температуры [т = /). Для уменьшения погреишости квазилинейной схемы следует уменьшать величину шага Дт, т. е. увеличивать число шагов по времени в рассматриваемом интервале. Поэтому во многих случаях оказывается более выгодным даже с точки зрения затрат машинного времени применять нелинейнук схему и делать более крупные шаги по времени Дт, выполняя на каждом несколько итераций.

Рассмотрим еще ОДИН получивший распространение иа пракпи1 способ построения итерационного процесса для решения систем нелинейных разностных уравнений. Этот способ основан иа линтр зации уравнений по методу Ньютона и обычно применяется в гол случае, когда зависимости коэффициентов от температуры заданы аналитическими зависимостями, которые могут быть продиффср цированы. Искомое значение температуры на текущей итерации "j представляется в виде

"« ~ Un -г IUn у

(37i

изменение температуры на s-й итерации, которое также

еизвестио и подлежит определению. Коэффи1""ь1 уравнений (3.67) ~ (3.69), зависящие от темпера-

пит f/*. заменяют следующими приближенными выражениями, вы-турь J: „ (5-!).

текающнмн из разложения в ряд Тейлора в точке и

(S-1)

In -f-

(s- 1)

f один из коэффициентов Х, q.. an, q, cci, qi. Производная вычисляется no значениям температуры иа предыдущей ите-

рации т. е. неизвестным в правой части (3.72) является т.чько Аи,,

Выражения (3,71) для температур и,," и (3.72) для коэффициент тоБ подставляют в систему нелинейных разностных уравнений (3.67). Затем, пренебрегая слагаемыми, содержащими {Аи[)-, получают систему линейных разностных уравнений относительно приращений Aun \ Эта система имеет также трехдиагоиальную матрицу и реишется методом прогонки.

Таким образом при линеаризации по методу Ньютона на каждой итерации решают задачу относительно приращений Аип, а затем вычисляют температуры иР согласно (3.71). Этот .метод имеет более высокую скорость сходимости по сравнению с методом последовательных приближений, по оказывается несколько сложней в про-

граммной реализации и требует вычисления производных , для

которых могут получаться громоздкие выражения.

Отличие алгоритма расчета по нелинейной схе.ме от описанного в § 3.5 состоит в том, что иа каждом шаге по времени организуется итерационный процесс, в котором вычисляются новые значения коэффициентов разностных уравнений и решаются методом прогонки системы разностных уравнений относительно ип (или Aun). Для этого в программе в цикл по времени следует «вложить» цикл по Итерациям (5 --- 1, k). Особенностью программной реализации является также то, что следует предусмотреть одномерные массивы длиной N для хранения следующих температур: - темпера-

""Уры предыдущей итерации данного шага повремени. -температуры предыдущего временного слоя; uj, температуры "•Ущей итерации (или приращения температур Auli), вычисляемые в процессе решения системы разностных уравнений. Алгоритм программы для решения задачи по нелинейной схеме с помощью "Юда простой итерации приведен иа рис. 3.10. Отметим, что после

ьшолнеиия каждой итерации содержимое массива температур ,Ун.й итерации следует перевести в массив температур преды-

Ущей итерации, а после вьшолнения каждого шага по времени

ёвод ucxodHh/x

dOHHblX

7 -- 1

Иочапа циппа по Времени

5 - 1 Начало итерации

Вычисление и т. о.

Вь/л/сление /коэффициентов г, Cn,dn

Подпрограмма SYSTRD

П = 1. ..А/ --Un

тт-1

Остомоб

имое массива температур текущей итерации в массив гем-рпятУР предыдущего временного слоя.

Нети"ейная схема можегбыть применена и для решения стаиио-X задач. В этом случае шаги по времени не выполняются, а инГпроводятся итерации до сходимости решения нелинейной сис-емы разностных уравнений, соответствующих стационарной зада-те системы {3.67) - (3.69) при ср - 0. В качестве начального

приближения можно, например, задать решение разностной схемы при постоянных коэффициентах, вычисленных при какой-либо постоянной температуре Т из рассматриваемого интервала изменения температур. Программа решения 1естационарной задачи но нелинейной схеме может быть использована для решения стацноиар-ион задачи, если положить ср - Г).

§ г.7. КОНЕЧНО-РАЗНОСТНЫЕ СХЕМЫ ДЛЯ МНОГОМЕРНЫХ ЗАДАЧ

Построение разностных схем. При построении разностных схем для многомерных задач обычно используется рассмотренный иышс метод баланса. Для его применения необходимо разбить исследуемую область на элементарные объемы. Очевидно, что по сравнению с одномерным случаем, где элементарный объем всегда является отрезком, здесь имеется гораздо Otubiiiee число видов этих объемов. Например, двумерную область можно разбить на элементарные объемы прямоугольной (рис. 3.11, а), треугольной (рис. 3,11, б) формы

Рис. ЗЛ 1

или какие-либо более сложные (например, рис. З.М. в). Вычислительная практика показала, что конечно-разностные схемы целесообразно, как правило, применять для элементарных объемов, ограниченных поверхностями, параллельными ортогональным координатным поверхностям. Для декартовых координат -- это прямоугольники в двумерном случае и параллелепипеды в трехмерном, полярных координат - кольцевой сектор и г. д. При использовании других элементарных объемов (в форме треугольников, Тетраэдров, призм с различной формой основаеи1н и др.) следует применять для численного решения задачи метод конечных элементов, рассматриваемый в главе 4, кaзaннoe обстоятельство на-адывает определенные ограничения на виды областей, для кото-

ln,ml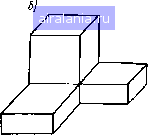

Рис. 3.12

рых применение конечно-размостиых схем наиболее эффективно с точки зрения удобства составления алгоритма расчета и его программной реализации. Эти области должны хорошо покрываться прямоугольниками нли параллелепипедами (рис. 3.12, а, б). Если область имеет криволинейную границу сложной формы, то задачу чаще решают методом конечных элементов.

Далее для наглядности будем рассматривать двумерный случай. Возьмем простеЙЕиую область прямоугольной формы (рис. 3.13), в которой требуется найти решение уравнения

XI

./л- ду- ;

с граничными условиями третьего рода

Яг {X, У)

(3.73)

дТ ди

(3.74)

и начальным условием

Тио-Т,{х, у).

рис. 3.13: {.V,,, Уга}п=и

(3.7.1)

Введем неравномерную простраиствепную сетку, показанную иа

71 =п + 1 ~Хп, hyjr, ----- Ут-i-l Ут

и равномерную сетку по времени. {тЛ/=о, - /Ат. Грани элемен-тарнь[х объемов разместим посередине между узловыми точками.

Сначала составим конечно-раз-ностиое уравнение для

.Ут)

ного точ-

Рнс, 3.13

либо внутреннего элементар объема, содержащего узловую i" Мы,У1 КХп,У.пУ от объем окру>к J- четырьмя соседними. Поэтому

отличие от равенства (3.50) в УР неиии теплового баланса слеДУ

гчнтывать не два, а четыре тепловых потока от соседних объемов, равнение баланса имеет вид

ср(Г/ -r/-)d/dx=

"i-i

""+1/2

- Pm+i /2 4 Prn-l /9. Ч" j f d I/ dx

Для расчета тепловых потоков Pn±i/2. Рт±\/2 используются выражения, аналогичные (3.44):

Рп+ \ /2 - Х

т-\ /2

Множители {hm + /im-i)/2 и (/г f h„y) I 2 соответствуют «площадям» граней элементарного объема, через которые проходят тепловые потоки.

Тогда для неявной схемы имеем

п. tn "n-i m

i - J

n. m-f-1 n . in

hn-x

71 +1/2 m+i. 3

\ qv{x,y)dydx.

(f,t +V -1)

(3.76)

Заменяя в правой чисти (3.76) индекс времени / иа {j - 1), по- Учаем явную схему.

С помощью метода баланса несложно составить пазностиые уравнения и для граничных элементарных объемов. При этом в Равнениях теплового баланса следует учитывать тепловые пото-На Границе области в окружающую среду, выражения для кото- вытекают из граничных условий (3.74). Например, для объема,