так же, как и в одномерном случае, действуют циклы для фор, мирования коэффициентов d,, разностных уравнений канонического вида, выполняются обращения к подпрограмме прогонки, и резул таг решения системы разностных уравнений для соответствующего кстержня» (температуры нз одномерного массива W) переписывается в трехмерный массив U.

Результаты расчета - температуры и/,, т. к - выводятся на печать в заданные моменты времени т в заданных сечениях перпендикулярных оси z. В каждом сечении выводятся все темпера!

туры и;,. k (« 1, N\ т 1, М). Сечения и моменты времени Ту задаются с помощью массивов KVV и TV.

ГЛАВА

МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ

ДЛЯ РЕШЕНИЯ ЗАДАЧ ТЕПЛОПРОВОДНОСТИ

§ &Л. ОСНОВНЫЕ КОНЦЕПЦИИ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ ]МКЭ)

Все рассмотрен[1ые нами ранее разностные схемы для решения уравнений теплопроводности являются реализациями метода конечных разностей. Системы алгебраических уравнений для определения численного решения мы получали путем за.мены производных в дифференциальном уравнении и в граничных условиях или в уравнениях теплового баланса для элементарных ячеек конечными разностями. Таким образом, в методе конечных разностей отправной точкой для получения приближе[Пшго решения является дифференциальная краевая задача. Однако искомое поле можно находить и из решения соответствующей вариационной задачи. На ее численном решении основан получивший lunpoKoe распространение метод конечных элементов (МКЭ) [7, 271. „

Сущность А1КЭ рассмотрим на примере решения двумерно станиопарной задачи теплопроводности в области D произволь пой юрмы (рис. 4.1):

д i дТ \ ох \ ох

дТ \

1ри граничных условиях третьего рода: ,

(4.1)

uc" - объемная и поверхностная плотности мощности ис-

теплопроводность; а- коэффициент теплоотдачи на Г)а-

.очииков теплоты

Величины/., а, могут быть заданы в виде произвольных

функций координат X, у, в том числе и кусочно-непрерывных функций-

Метод конечных элементов основан на определении температур-[loro поля путем приближенного решения соответствующей вариационной задачи. Для формулировки этой задачи напомним поня-fiie функционала. Оператор / [/ (х)] называется функционалом, заданным иа некотором множестве функций, если каждой функции f(A)H3 этого множества по некоторому правилу ставится в соответствие числовое значение / [/ (х)\. Иными словами, функционал является как бы «функцией от функции». В практических приложениях обычно встречаются функционалы, заданные в виде некоторых интегралов, в подынтегральные выражения которых входят функции / (х).

Многие краевые дифференциальные задачи теплопроводности н конвективного

теплообмена эквивалентны задачам отыскания функций, доставляющих минимум некоторым специально сконструированным функционалам. Задача на отыскание функции, минимизирующей функционал, называется вариационной. На основе перехода от краевых дифференциальных задач к вариационным развиты многие приближенные аналитические методы решения задач теплопроводности. Сними можно познакомиться по книгам [3, 6, 11]. Отметим, что возможность вариационной формулировки задачи определения температурного поля (4.1), (4.2) обусловлена свойствами дифференциального оператора уравнения теплопроводности [ 11 ]. Вд Приведем вариационную формулировку рассматриваемой краевой дифференциальной задачи (4.1), (4.2) без доказательства. Зада-3 решения уравнения (4.1) с граничными условиями (4.2) эквива-HTTia задаче определения функции Т (х, у), минимизирующей нкционал /[Г (X. у)] вида

Рис. 4.1

дТ V

дх J \ ду + J(ar-2, r)d/.

(4.3)

нног- широко распространенный прием получения прибли-

блц решения вариационных задач состоит в следующем. При-ие для искомой функции Т (х, у) разыскивается в виде

2217

Т{х, У) « 2 ""/"(•У)

(4.4)

подстановке в аппроксимацию (4.4) координат т-го узла (л: =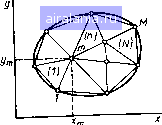

Рис. 4.2

где - неизвестные постоянные коэ4)фнцненты, а (х, у) вестные функции пространственных координат. Если подставить (4.4) в функционал (4.3), то можно провести интегрирование по пространственным переменным н получить величину /, завнсящу] уже не от неизвестной функции, а от неизвестных коэ4х1)нциентов разложения (4.4):

/ - }{а,, ...,ам). (4.5)

Очевидно, что для определения приближенного решения вариационной задачи в виде (4.4) следует найти значения а, ам, обес-

печнвающне минимум функции (4.5), т. е. задача сводится к отысканию точки минимума «обычной» функции нескольких переменных. Как известно, значения а,. ам, обеспечивающие минимум функции /, находятся из решения системы уравнений

д} а/

7-0....,0. (4.6)

Решив систему (4.6), можно найти значения а, ам н, подставив их в (4.4), ОП редел нть п р нбл нжен ное реше-нне вариационной задачи. Центральным местом в изложенном методе является назначение координатных функций разложения (4.4) /i, /м. Метод конечных элементов основан на использовании описанной схемы приближенного решения прн специфическом выборе вида координатных функций /ь ...,/л1. Благодаря этому выбору неизвестные коэффициенты в разложеннн (4.4) приобретают ясный физический смысл.

Построение координатных функций проводится в МКЭ после разбиения области определения искомой непрерывной величины на N подобластей, называемых элементами, и фиксации в них М узловых точек, выбираемых на границах элементов (см., например, рнс. 4.2). Отметим, что число членов в разложении (4.4) равно числу узловых точек. Каждая из функций (х, у) обладает следуют свойствами. Значение функции (х, у) в т-й узловой точке с ординатами х = х, У = Ут равно единице, а в остальных уз вых точках - нулю. Кроме того, функция (х, у) может быть лнчна от нуля только в элементах, содержащих т-й узел. В ост ной части области D она считается равной нулю. л й нС"

При таком выборе координатных функций (х, у) yyo-

известный коэффициент в разложеннн (4.4) равен "Рно. му значению температуры и„, в т-й узловой точке. Действите

X , у - Ут) значения всех координатных функций, кроме т-й jjVHKUHH, будут равны нулю, а значение т-й функции - единице и, едовательно,

Т{Хт, Ут) «т (« У" "mfma-

(4.7)

При использовании разложения (4.4) в каждой точке области D «работают» только те координатные функции, у которых коэффициенты равны приближенным значениям температур узловых очек конечного элемента, содержащего данную точку.

Отметим два важных факта, вытекающих нз рассмотренных свойств координатных функций.

Во-первых, функция / (а,, ам), получающаяся прн подстановке разложения (4.4) в функционал (4.3), будет функцией от неизвестных приближенных значений температуры в узловых точках Ui, .... "л*:

/-/(И1,...,ыл,), (4.8)

а уравнения, вытекающие нз условия минимума (4.6),

а/ а/

-О.....

(4.9)

будут алгебраическими уравненнямн разностной схемы метода конечных элементов относительно искомых температур в узлах.

Во-вторых, пространственное распределение температуры внутри любого элемента аппроксимируется суммой произведений координатных функций на коэ4х1)нциенты, равные приближенным значениям температуры в узловых точках, принадлежащих данному элементу.

Координатные функции (х, у), т \, М строятся на основе так называемых функций формы элементов. Каждая нз функций формы конкретного элемента равна единице в одной «своей» узловой точке, принадлежащей данному элементу, н нулю в остальных узлах этого элемента, т. е. для элемента вводится столько функций формы, сколько в нем содержится узлов. Вне элемента все его функ-ии формы считаются равными нулю. Таким образом, функция фор-п-то элемента, равная единице в принадлежащей ему т-й точ- яется «представителем» координатной функции (х, у) в ritvT элементе. Поэтому температурное поле в д-м элементе ап-gfPycTCfl суммой произведений его функций формы на при-ijbie значения температур в его узловых точках. Очевидно, fpa/ •каждого элемента получается своя аппроксимация, но на ицах элементов должна сохраняться непрерывность темпера-•Риого поля.

(4 2РДм к реализации изложенной методики для задачи (4.1),

§ 4.2. ПОСТРОЕНИЕ ДИСКРЕТНОЙ МОДЕЛИ И ФУНКЦИЙ ФОРМЫ ЭЛЕМЕНТОВ

Первый этап численного решения задачи методом конечных эле-ментов включает выбор вида элементов и способа расположения g них узловых точек, разбиение области на элементы и размещение узлов, а также определение функций формы. Отметим, что эти функции существенным образом зависят от вида используемых элементов и способа расположения узлов. При решеиин двумерны.х задач

1 г 3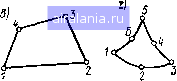

Рис. 4.3

применяют Элементы различной формы (рис. 4.3, а - г): треугольные, четырехугольные, элементы с криволнненными границами, с узловыми точками, расположенными по границам элементов. При ре-уиении трехмерных задач элементы могут быть выбраны в виде тетраэдров, косоугольных параллелепипедов, призм с треугольным ос-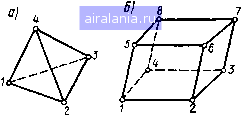

Рис. 4.4

нованнем (рнс. 4.4, а - Ь). Ниже ограничимся рассмотрением наиболее простых и часто применяемых линейных треугольных эле-.ментов с узлами, расположенными в их вершинах (см. рис. 4.3, 4 Название «линейные» у этих элементов обусловлено тем, что пр" наличии на границе трех узлов допустимо использовать только функции формы F (х, у), линейные по координатам хну:

f{x,y) = a + bxcy. С-]

Три коэффициента а,Ь ц с определяются нз трех условий: в ДбУ вершинах значения F (х, у) равны нулю, а в одной - едкн"" Применение более сложных элементов позволяет нспользовать

аппроксимации температурного поля в элементе полиномы более высоких степеней. Например, для треугольного элемента с шестью узлами (см. рис. 4.3, б) нужно применять более сложные по сравнению с (4.10) функции формы вида

F (х, у)=а -г Ьх су-с А ху-\- ех + fy.

(4.11;

Отметим, что при построении функций формы кроме сформулированных выше условий на их значения в узловых точках (единица в одном узле н ноль в остальных) необходимо обеспечивать непрерывность аппроксимации на границах смежных элементов. Методика лопучения функций формы для различных видов элементов рассмотрена в [7, 27].

Итак, разобьем двумерную область D иг N треугольных элементов и введем М узлов во всех вершинах треугольников (см. рис. 4.2). Причем вершины одних треугольников не должны находиться на сторонах других треугольников, т. е. каждый элемент должен содержать три узла. Присвоим сквозную нумерацию всем элементам [п --- I. N) и всем узлам (т = 1, М). Номер узла в ойцем случае не связан с но.мером элемента. Вопрос об оптимальном способе нумерации узлов обсудим далее.

На рис. 4.5 отмечен некоторый д-й с»лемент, содержащий вершины с номерами г, /, /г, которые могут принимать значения от I до М. Эти узлы имеют координаты Xt, Xj, Х), пооси х и У(, у, у поосн у.

Выполненное разбиение удобно описать для дальнейшего использования в программах следующим образом:

задать массивы координат всех узлов {x}=i и {ут)т = \ в порядке их нумерации;

указать для каждого п-то элемента по три номера узлов, лежащих в его вершинах;

указать для каждого п-го элемента признак, определяющий принадлежность его сторон внешней границе области D.

Номера узлов в вершинах и признаки принадлежности сторон раиице будем задавать в виде следующей таблицы:

Кот " таблицу можно задать в виде матрицы размером N х4, оторую будем называть индексной матрицей. Номера узлов i, /, k индексной матрице будем записывать в порядке, соответствующем стн элемента против часовой стрелки. Признак принадлежно-сторон границе принимает значение О, если стороны элемента не легают к внешней границе; значение 1, еслн граничной является