

|
|
Главная -> Применение эвм 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 [21] 22 23 24 25 26 27 28 29 30 31 32 33 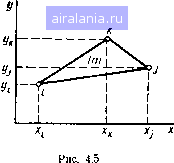 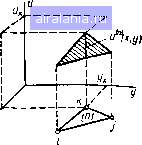 Рис. 4.6 сторона между узлами i и /; значение 2, если граничными являются две стороны - между узлами / и / и между узлами / и k. Ясно, чтх> других ситуаций можно избежать путем соответствующего выбора узла 1. с которого начинается запись номеров в строке индексной матрицы. Предложенный способ полностью описывает выполненное разбиение на элементы и нумерацию узлов н не содержит избыточной информации. Искомыми величинами в МКЭ являются приближенные значения температуры Um в узлах т = \, М. Согласно основной идее метода распределение температуры в каждом элементе представляется в виде суммы, в которую входят три функции формы элемента, умноженные иа приближенные значения температуры в его трех узловых точках. Поэтому распределение температуры в п-м треугольном элементе и" {х, у) имеет вид (рис. 4.6); ui"Hx, y)=UiFl"Hx, y)UjFf){x. У)+"лП"(л-, у), Ct) где FT\ FT\ Ff - линейные функции координат х, у вида (4.9), равные единице в узлах /, / или k соответственно н равные нулю в двух других узлах (рис. 4.7), Индекс (п) указывает, что функции формы относятся к п-му элементу. 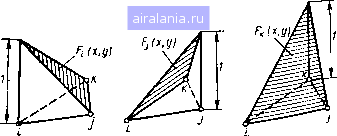 Рис. 47 Таким образом, для функции формы [х, у) должны выпол- няться равенства FlHXu Уг)=-\, /=;."> (;. f/j)=/<."(A. Уи)=0. (4.13) Аналогичные соотношения имеют место и для двух других функций f*."* {X, f/)> Н" {Х-, у)- Используя условия (4.13), можно выразить коэффициенты ат\ Ь, с"* {т = i, /, k) через координаты узлов I, /» " определить функции формы. Приведем выражения для этих коэффициентов. Здесь и далее индекс элемента (п) будем опускать, помня, однако, что функции формы различны для каждого элемента. Из условий (4.13) следует: = {Х}Ук - ХкУ})125 {yj-yu)/2S {ХкУ1~Уь Xi)/2S (ak=-{Xiyj - Xjyi)J2S --{yk-yi)l2S = (Xi-x,)/2S bu-{yi-yi)!2S W--{x~Xi)!2S, (4.14) где5 - площадь треугольника, значение которой может быть вычислено через координаты узлов: S = {X}Уи - ХиУ} + У:Xi~уXi + х„ У; - Xjyi)/2. (4.15) Градиент температуры в каждом элементе имеет постоянное значение, и производные по координатам определяются соотношения- =biUibjuj + 6 и,,, - =CiUi-cj uj + сиь- (4.16) дх ду При выводе разностных уравнений МКЭ иам понадобится вычислять интегралы по площади треугольника и по отдельным сторонам от выражений, содержащих функции формы. Приведем ряд используемых в дальнейшем формул. Интеграл по площади элемента от любой его функции формы равен ]рт\х, ,v)dxd = SW/3, m = /, k. (4.17) Как видно нз рис. 4,7, этот интеграл равен объему пирамиды с треугольным основанием и высотой, равной I. Интегралы по стороне Ly вычисляются по формулам: J Fi{x, y)dlLi}/2, J F!{x, y)dl = Lij/3, I] I Pi{x, y)Fj{x, y)dlLi}/6, (4.18) Лами- ~ ~ ~У} ~~ Д-ина стороны между уз-PmwV" Данные выражения справедливы для всех функций ь F. § 4.3. СИСТЕМА УРАВНЕНИЙ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ. ЛОКАЛЬНАЯ И ГЛОБАЛЬНАЯ МАТРИЦЫ Перейдем к следующему этапу - составлению системы разнос ных уравнений МКЭ. Система уравнений для определения темпп тур в узлах {Ujn}m=\ составляется на основании условий mhhhmv ма функционала (4.8). Этот функционал можно представить в виде суммы интегралов по всем элементам, на которые разбита область «= 1 (4.19) { ди \ { ди dxdy- (4.20) Второй интеграл в (4.20) вычисляется лишь для граничных элементов вдоль тех их Сторон, которые прилегают к внешней границе L области D. Условия минимума функционала можно с учетом (4.19) переписать в виде п= 1 = 0, т=], М. (4.21) Структура системы разностных уравнений. Рассмотрим подробнее Структуру системы разностных уравнений (4.21). Возьмем /77-е уравнение, получаюш,ееся прн дифференцировании функционала (4.19) по значению температуры в т-м узле. Напомним, что распределение температуры ы" [х, у) в любом элементе зависит только от температур щ, Uj, Uk в узлах этого элемента. Соответственно н значение функционала /t) зависит только от этих температур. Поэтому в сумме (4.19) от будут зависеть только i элементов, которые включают т-й узел. Это обстоятельство юзв0-ляет формировать систему (4.21) одним нз двух способов. Первый способ основан иа переборе узлов. Он заключается в выделении какого-то т-го узла, определении элементов, содержащих Этот узел, н суммировании частных производных от функционалов этих элементов по температуре выделенного узла. Таким образом, при получении системы (4.21) последовательно формируется первое, Второе, .... М-е уравнения. Второй способ основан на переборе элементов. В этом случа выделяется какой-то п-й элемент и три производные от функциона- этого элемента по его узлам заносятся в левые части соответст-""lOiUHX трех уравнений системы (4.21), т. е. производится формирование сразу всей системы, которое реализуется путем посте- нного «наращивания» левых частей уравнений. Этот способ по-"учил более широкое распростраиенне н рассматривается инже. Очевидно, что для его реализации понадобятся выражения для поизводных от функционала п-го элемента по температурам еро узлов Ui, Uj, Uk. Для нх получения поменяем порядок дифференцирования н интегрирования, т. е. сначала проведем днффереицн-пованне подынтегрального выражения в (4.20), а затем вычнслнм интеграл по элементу от получившейся функции. Прн реализации этой процедуры будем использовать выражение (4.12) для распределения (х, у), причем индекс (п) для сокращения записей опустим. Учитывая выражения (4.16) для производных, имеем / ди дх } ( ди \- 2{biUi + bj Uj-\-buUk)bu dui д dui 2{CiUiCj Ujt\ u)Ci, {2qu)2qFi{x, у), {2q,u) = 2qsFi{x, y). (4.22) [au] - 2a [Fi щ. -iFjUj F u) Ft. Будем считать, что разбиение выполиеио таким образом, чтобы величины Я,, а можно было бы считать постоянными в преде- лах каждого элемента. Если эти величины являются кусочио-не-прерывнымн функциями координат, то разбиение проводят так, чтобы границы элементов совпадали с линиями разрыва. Если величины являются непрерывными, но резко изменяющимися функциями координат, то нужно построить в области нх сильного изменения более густую сетку. Вычислим сначала интеграл по площади элемента, используя выражение (4.17) для интеграла от функций формы: I ди , дх I ди ~ 2qu dxdy = 2 [X (bi Ui -b,Uji- bh Uk) bi + X (Ci Ui + cjuj + u) Ci- Qv Pt (x, y)] dxdy 2S() [X (6? Ui + bt bj Uj + bi b w) + + X{c! Ui+CiCjUj-\-CiChUk) -qjSl (4.23) Если стороны элемента принадлежат границе области, то в фуц кцнонале следует учесть интеграл по этим сторонам. Пусть границ" ной является сторона 1ц между узлами г и /. Тогда с учетом выр. жений (4.18) для интегралов по сторонам от функций формы полу чаем: {au-2q,u)dl = f 2{{Fl щ +FiF jUj)-q,F-М - 2Lij i<xUi/3 -h auj/6 gj2). (4.24) Здесь учтено, что Fk (x, у) О на стороне Lij (см. рис. 4.7). Если граничной является сторона Ln,, то выражение для интеграла запишется аналогично, но вместо Lu следует подставить Lj. а вместо - Mft. Если же к границе прилегает сторона Ljh, то рассматриваемый интеграл равен нулю, так как функция формы (х, у) для узларавна нулю на стороне Lj н, следовательно, распределение температуры на этой стороне не завнснт от температуры и/. Таким образом, окончательно получаем для производной от функционала /<" по температуре м,-следующее выражение: = SCi (bt Ui -f bi bj Uj + bi bk u + cf Ui + Ci c щ + Ci CkUi,)+ altj(Ui/3 + U;/6) + aLik («с/З + u,j6} - -q, S(")/3 q, Lij/2-q, 2, (4.25) причем слагаемые с Lij н Li записывают лишь в том случае, когда соответствующие стороны принадлежат границе. Аналогичным образом можно получить и выражения для производных от по температурам Uj н и. Проанализируем теперь с учетом (4.25) структуру системы (4.21). Видно, что производная dHVdui представляет собой сумму произведений неизвестных температур и,-, Ыу, uu на постоянные известные коэффициенты, завнсящне от координат узлов и параметров задачи, а также постоянных известных членов, не зависящих от искомых температур. Левые части уравнений (4.21), получаемые путем суммирования частных производных, имеют такую же структуру, н, следовательно, приравнивая нх нулю, мы получаем линеи- ную систему разностных уравнений относительно неизвестных тем ператур узловых точек. Локальные матрица и вектор-столбец. Для формирован матрицы лниейной системы разностных уравнений удобно запис полученные выше соотношения для частных производных фун. нала п-го элемента в матричном виде. Для получения матричной пнсн принято использовать так называемую локальную нУР,. узлов н соответствующих нм неизвестных температур, •я-щую только в рамках каждого конкретного элемента разбие Остановимся на этом подробнее. Возьмем п-й треугольный эле-jeHT разбнення, имеющий трн узловые точки с «глобальными» номерами /, /. к, н будем условно считать в рамках п-то элемента i-н узел - первым, /-й узел - вторым, а k-a узел - третьим. Соответственно введем локальные номера 1,2,3 для неизвестных температур И(. "j. "ft в узлах этого элемента н будем использовать следующие обозначения: Ы;-Ы<", Uj-4«>, ы,-ыЧ (4.26) Отметим, что соответствие между глобальными н локальными номерами для каждого элемента разбнення задается с помощью индексной матрицы, о которой шла речь в § 4.2. При нспользованнн локальной нумерации выражения для частных производных от функционала в п-м элементе можно записать следующим образом: (4.27) где g" -матрица размером 3x3; трех элементов: ие»), - столбцы из а/С)
0(1) gin) 0(1) pin) &з1 Saa баз (4.28)
Из выражений вида (4.25) вытекают следующие формулы для элементов матрицы g(") н вектора ср": gin) (й? + ф XS<") + {aL,j + aL,ft)/3, g[V = {bibj + CiCj)XSi-) g{V = (bibk-\CiC„)XSfi+ aLik/6, giV = [bJ + c}) XS("> + (ccL.j + aLfyS, giV=(bJbk + CJC„)XS>+ aLj, gif-g[Vr (4.29) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 [21] 22 23 24 25 26 27 28 29 30 31 32 33 0.0079 |