

|
|
Главная -> Применение эвм 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 [22] 23 24 25 26 27 28 29 30 31 32 33 o(rt) = ai") - q, S*)/3 + (t/, Lij + L)/2, 4.(3") - q, S(")/3 + Lift -f (7« L,)/2. (4,30) В выражениях (4.29), (4.30) для элементов матриц gti „(л, слагаемые, содержащие множители L, Lj, Lj,, следует учитывать лишь в том случае, еслн соответствующая сторона элемента п прн, надлежит внешней границе L, Ясно, что матрица системы линейных уравнений относительно неизвестных температур {u,n}m=i будет формироваться на основе матриц g<"i, а вектор-столбец свободных членов - на основе векторов-столбцов (р(". Матрицу gc* часто называют локальной матрицей жесткости нли локальной матрицей теплопроводности, а вектор q)("- лолгйль-ным вектором нагрузок нли локальным вектором тепловых потоков. Термины «жесткость» и «нагрузка» используются исторически потому, что сначала МКЭ развивался применительно к задачам прочностного расчета, В задачах теплопроводности в матрицы g*") входят теплопроводности X и коэ4хнциеиты теплоотдачи а, а в векторы q)" - свободные члены неоднородного уравнения теплопроводности и граничных условий, т. е. объемные и 1юверхност-иые плотности теплового потока источников теплоты. Геометрические параметры расчетной области учитываются коэффициентами Ьт \ Ст функций формы элсмента, а также значениями L;,, Lj, Если рассмотреть предельно крупное разбиение, при котором вся область состоит лишь из одного элемента {N = I), то система уравнений для определения трех неизвестных температур его узлов будет иметь вид где g*, <р<4 - локальные матрица и вектор-столбец первого н единственного элемента, т- е, в случае разбиения, состоящего из одного элемента, его локальные матрица и вектор-столбец совпадают с матрицей и вектором правых частей линейной системы ур иеинй МКЭ. Глобальные матрица и вектор-столбец. В реальном случае, когда в разбиение входят N элементов, эти матрицы и вектор-стобш естественно ие совпадают. И в связи с использованием термина «ДО кальный» для матрицы и вектор-столбца элемента матрица и вектор- свободных членов снЬз-емы уравнений для всей области иа-:то-" глобальными. Эту сиЬуему будем записывать так:
(4.31) j-де G - глобальная матрица жесткости (теплопроводности) разме-jjjXi; и - вектор-столбец искомых значений температур в М узлах; Ф - глобальный вектор-столбец нагрузок (тепловых потоков). На первый взгляд введение дополнительной локальной нумерации неизвестных в элементах разбиения и использование матричной формы записи (4.27) представляется излишней процедурой. Однако, как показала практика, на самом деле это позволяет сделать более удобной процедуру формирования глобальной матрицы G и вектор-столбца Ф при составлении программ расчета по методу конечных элементов, § 4.4. ФОРМИРОВАНИЕ ГЛОБАЛЬНЫХ МАТРИЦЫ И ВЕКТОР-СТОЛБ14А. РЕШЕНИЕ СИСТЕМЫ УРАВНЕНИЙ МКЭ Прежде всего отметим, что процедура построения уравнений в МКЭ имеет важную особенность по сравнению с методом конечных разностей. Прн построении конечно-разностной схемы мы рассматривали уравнение теплового баланса для элементарного объема, построенного около узла сеткн с номером (см. § 3.3), и сразу получали т-е уравнение общей системы. В случае МКЭ в пье уравнение системы (4.21) входит сум-«а производных от функционалов /с, вычисленных для различных элементов, которое содержат узел с номером т. Поэтому при составлении каждого уравнения надо производить суммирование «вкладов» от разных элементов. Из-за этой особенности роцедура построения системы уравнений КЭ нескол ько менее нагл ядна, чем в УЧае конечных разностей, и прн ее пер-Оачальном нзученнн возникают некоторые трудности. Для про-стоты изложение начнем с разбора конкретного примера для ооласти, изображенной на рис, 4.8 и состоящей всего из трех эле-Нтов, которые содержат пять узлов. Пример построения системы разностных уравнений, Нумера-Элементов, глобальная и локальная нумерация узлов приведе- 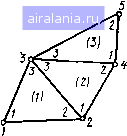 Рис. 4.8 ны на разбиен рис. 4.8- Индексная матрица,/ответствующая выбран нию н нумерациям, имеет виД; *biM
Соответствие между глобальными и локальными обозначениям неизвестных температур имеет вид: 1 -«1, «; «4, <*=U5, U" (4.32) «о. Теперь рассмотрим структуру глобальной матрицы и глобального вектор-столбца. Начнем с первого уравнения. Поскольку узел / содержится только в первом элементе, то в первом уравнении (4.21) остается только частная производная от функционала первого элемента н оно принимает вид В соответствии с (4.27), (4.28) в локальных координатах это уравнение записывается в виде Для первого элемента локальные и глобальные номера совпадают [см. (4.32)1 н поэтому окончательно первое уравнение системы записывается так: Отсюда вытекает, что>, g[\ и g[\ являются первым, вторым и третьим коэффициентами первой строки глобальной матрицы G, а чр**~ первым коэффициентом глобального вектор-столбца: Gv=ig[\\ g[\\ g[[\ О, 0). Ф, = ф(1>. Сложнее обстоит дело со вторым узлом, принадлежащим ДвУ** элементам 1 п2. Второе уравнение системы имеет вид ьз (4-27), (4.28) вытекаетлчто в локальных обозначениях неиз-ных это уравнение записывается следующим образом: g[V <+g[\ «-ф1» + + g[V "i «г" ф(2>- 0. Обратим внимание, что при записи -5/(>/5u2 использованы ко-аЛкЬнЦиенты первой строки локальной лЫтрицы и первый коэффи-столбца для второго элемента, поскольку температура «2 в локальных обозначениях имеет первый номер: и. = и[- Те-еоь получения искомого уравнения необходимо в соответст-длй С (4.32) заменить локальные обозначения неизвестных на глобальные: ф" + 11«4 + <Гз*"з~Ф-0. (4.33) (4.34) Группируя слагаемые с одинаковыми неизвестными и складывая постоянные коэффициенты, получаем вторую строку глобальной матрицы G и второй коэффициент глобального вектор-столбца Ф в виде G2j = {g[\K gi[ + g[V, 1з + ?11. g[\K 0). Аналогичным образом можно получить и остальные три уравнения. Алгоритм формирования глобальных матрицы н вектор-столбца. Полученные выражения (4.34) позволяют изложить принцип формирования т-го уравнения глобальной системы. Это формирование целесообразно проводить путем постепенного суммирования вкладов от различных элементов. При машинной реализации перед началом формирования массивы, в которых помещаются глобальные G и Ф, обнуляются, а затем к их текущим значениям постепенно добавляются соответствующие коэффициенты локальных матриц и столбцов. Ясно, что вклад в т-е уравнение системы дадут только те элементы, у которых в строке индексной матрицы имеется номер т. Если т-й узел числится в локальной нумерации какого-либо нз этих элементов /-м (/-1, 2 илн 3), то будет использована •й строка локальной матрицы gt" и 1-й коэффициент локального вектор-столбца ф(" Найденный нужный коэффициент локального столбца прибавляется к текущему значению т-го коэффициента глобального столбца. Коэффициенты выделенной строки локальной матрицы элемента прибавляются к соответствующим коэффициентам т-й строки глобальной матрицы, имеющим порядковые номера. Указанные в строке индексной матрицы, т. е. первому коэффнциен- У строки локальной матрицы соответствует первый номер «отсылки» в строке индексной матрицы, второму коэффициенту - второй омер третьему - третий. Описанная процедура лежит в орнове алгоритма формипп глобальной матрицы и глобального вектор-столбца. Как быю""" отмечено выше, она реализуется элементов следующим ализуется путем последовательного перео образом. Берется первый элемент, aHanJ руется его строка в индексной матрице и устанавливается, в к» три уравнения этот элемент «дает вклад». Далее рассчитываются локальная матрица и век тор-столбец. При этом расчете использу ся информация о наличии у данного элемента граничных стоппи содержащаяся в четвертом столбце индексной матрицы. Пусть ло кальным номерам 1, 2, 3 соответствуют фактические номера [, у Тогда первая строка локальной матрицы и первый коэ()фнцц,. локального вектор-столбца участвуют в формнрованнн :-й стпо ки глобальной матрицы и г-го коэффициента глобального вектоп-столбца. Производится сложение найденных локальных коэсх})ицн-ентов g\\K glV.gia с имеющимися значениями глобальных коэффициентов Gii, Gij, Gih. Затем аналогичная процедура повторяется для второй и третьей строк локальной матрицы н второго и третьего коэффициентов локального столбца. Они участвуют в формировании строк глобальной матрицы и коэффициентов глобального столбца с номерами / и к, которые соответствуют локальным номерам 2 и 3. Изложенный на примере треугольных элементов разбиения метод формирования глобальных матрицы и вектор-статбца, основанный на введении локальной нумерации узлов и неизвестных, легко переносится и на случай более сложных элементов разбиения. Он является наиболее общим, часто используемым н тем более -эффективным, чем сложнее применяемые конечные элементы. Свойства системы разностных уравнений н методы ее решения. Теперь рассмотрим ряд важных свойств, которыми обладает гла-бальная матрица. Во-первых, можно доказать, что она является симметричной. Во-вторых, глобальная матрица для задач большой размерности М является сильно разреженной, т. е. большинство ее элементов - нулевые. Наконец, путем введения разумной нумерации узлов ее можно сделать ленточной. Остановимся на двух последних свойствах матрицы. Очевидно, что коэффициент Gjj в т-й строке глобальной матрицы отличен от нуля, только когда узлы с номерами т и / являются вершинами какого-то общего для них элемента. В этом случае в строке индексной матрицы, соответствующей этому общему элементу, будут держаться номера т. н /. Укачанное обстоятельство и объясняет разреженность глобальной матрицы, поскольку, например, Д- треугольных элементов при значительном числе треугольников большинство возможных пар узлов m и /е не являются вершинами общего треугольника и, следовательно, соответствующий элемент глобальной матрицы Gjnk = О- Рассмотрим влияние нумерации узлов иа структуру глобальной матрицы G. Из сказанного выше вытекает, что расположение ну-~ элементов в матрице зависит от способа нумерации узлов. На-мер в рассмотренном BbiV конкретном примере при нумера-указанной на рис. 4.8, глЬ.бальная матрица G выглядит так: 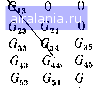 55 (4.35)
Если же перенумеровать узлы так, как это сделано на рис. 4.9, те матрица G примет вид (4.36) Обшее число пулевых элементов в (4.36) не изменилось яо сравнению с (4.35), однако в (4.35) ненулевые элементы расположены лишь на главной диагонали и на двух прилегающих к ней верхних и нижних диагоналях, а в (4.36) эти элементы ({разбросаны» по всей матрице. Таким образом при разумной нумерации узлов глобальная матрица G имеет ленточный вид, т. е. все ненулевые коэффициенты расположены в пределах полосы, образованной рядом верхних н нижних диагоналей, примыкающих к главной диагонали. Из симметрии матрицы следует, что число верхних и нижних диагоналей с отличными от нуля коэффициентами одинаково. Поскольку для треугольного ра.збиения коэффициент Gfe отличен от нуля только в случае, когда узлы тик принадлежат одному треугольнику, то положение наиболее удаленного от главной ди-згоцали ненулевого элемента матрицы определяется мгксималь-ой по всем парам общих вершин треугольников разностью номеров у:*лов, 7. е. величиной L=iuax\m~k\, (4.37) >п, к ~ номера узлов п-го треугольника. Схематичный вид глобальной ленточной матрицы показан иа 4.10. Символами «Х)> обозначены ненулевые коэффициенты. *се Коэффициенты, расположенные за пределами полосы, ограни- 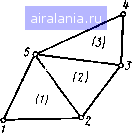 Рис, 4.9 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 [22] 23 24 25 26 27 28 29 30 31 32 33 0.024 |