хх О X X X о X о О о\ XXX X X X X о X О О X О X X X О

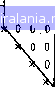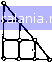ченной линиями, параллельными глажюй диагонали, равны нулю В общем случае нулевые коэффициенты встречаются и внутри полосы. Число (4-1) будем называтьjaupuHou полосы (шириной ленты) матрицы. /

Ленточный характер и симметрия глобальной матрицы позволяют значительно сократить объем машинной памяти, требуемой для ее хранения. При программировании задачи предусматривают запись матрицы не в виде массива длиной /И хМ, а в виде массива, содержащего лишь элементы, находящиеся в пределах полосы на главной диагонали и выше. Например, если требуется решить задачу

с числом неизвестных узловых температур уИ = 300, то для записи матрицы в общем виде необходимо хранить 300x300=9-10 вещественных чисел. Пусть ширина ленты в этой задаче равна L-f-l = 40. Тогда запись матрицы в сокращенном виде потребует массив длиной (L + 1) М = = 1,2-10* элементов, если матрицу запоминать в виде «прямоугольника» с L -f 1 столбцами и М строками, т. е. для облегчения логики программирования предусматривать место для L Хранения фиктивных элементов в последних L строках (заштрихованный

Рис 4 IП

треугольник вне матрицы иа

рис. 4.10). Если же не учитывать фиктивные элементы «хвоста», то потребуется запомнить [(L + 1) X хМ - L{LAr 1)/21 = 1,12-10* чисел.

Наконец, перейдем к вопросу решения системы уравнений. Для решения систем уравнений МКЭ применяют как прямые, так и итерационные методы. Причем последние обычно используют в тех случаях, когда объем оперативной памяти не позволяет хранить всю глобальную матрицу даже с учетом ленточного симметричного вида. Из прямых методов хорошо зарекомендовал себя на практике и получил широкое распространение метод квадратного корня. Этот метод пригоден только для систем линейных уравнений с симметричной матрицей и по затратам машинного времени примерно вдвое быстрей метода исключения Гаусса. В математическом обеспечении ЭВМ имеются стандартные программы, реализующие метод квадратного корня. Предусмотрен и случай систем с ленточной матрицей (стандартная подпрограмма МСНВ из математического обеспечения ЕС ЭВМ [151). В заключение подчеркнем, что испо1Ь-зование той или иной стандартной подпрограммы решения системы уравнений требует определенного способа записи глобальной матрицы в од1юмериый массив. Применяемые способы различны для разных подпрограмм, т. е. может .организовываться запись по 146

.покам или по столбцам, с>негом или без учета «хвоста» ленты, oi, обстоятельство следует учитывать при программировании алго-итма формирования глобальном матрицы.

i.5. ПРОГРАММНАЯ РЕАЛИЗАЦИЯ МК

Существенным достоинством МКЭ является возможность составления программ численного расчета полей в областях сложной геометрической конфигурации, которые проще цо логической структуре и по заданию исход}!ых данных, чем программы, реализующие метод конечных разностей для таких областей. В данном подразделе рассмотрим в качестве примера структуру программы для решения двумерной задачи (4.1), (4.2) в областях произвольной формы при треугольных элементах разбиения.

В программе решения задачи методом конечных элементов выполняются следующие основные процедуры:

1. Разбиение области на элементы, нумерация элементов, глобальная и локальная нумерации узлов и формирование на их основе индексной матрицы.

2. Формирование глобальных матрицы и вектор-столбца системы алгебраических уравнений, реализуемое на основе расчета локальных матриц и столбцов.

3. Решение системы разностных уравнений.

4. Расчет температур и тепловых потоков в различных точках элементов разбиения, проводимый на основе принятой аппроксимации температурного поля в элементе.

Остановимся на особенностях программной реализации первых двух процедур, рассматривая их применительно к решению задачи (4.1), (4.2).

Автоматизация разбиения области. Простейший (но наиболее трудоемкий)способ реализации первой процедуры состоит в ручном разбиении области D на треугольные элементы, ручной нумерации узлов и дальнейшем вводе в качестве исходных данных массивов Координат узлов {Хга)т=\, « индексной мэтрицы. Однако

в реальных двумерных (и тем более трехмерных) задачах число уз-•ов и элементов может составлять несколько сотен, а иногда и ты-яч, и поэтому построение расчетной сетки вручную и ввод боль-4JHx массивов чисел в качестве исходных данных нецелесообразны 3"3а значительных затрат времени на их подготовку и большой вероятности появления ошибок. Следовательно, возникает задача ав-"матизации процедуры разбиения области на элементы, нумерации элементов и узлов и формирования индексной матрицы. При том требуется в качестве входной информации для соответствую-подпрограммы задавать сравнительно небольшое число дан-описывающих геометрию области сложной формы и густоту "•"н, а на ее выходе получать массивы координат узлов и индекс-

формированию глобальной

ной матрицы, позволяющие перейти матрицы системы уравнений МКЭ.

Для областей типа прямоугольника, треугольника или некоторых более сложных, но конкретных конфигураций можно составить частные подпрограммы, реализующие заполнение массивов координат узлов н индексной матрицы на основе данных о размерах области и шагах по осям х, у. Например, можно покрыть область прямоугольной сеткой, а затем построить треугольники путем разбиения элементарных прямоугольников диагоналями, как это сделано иа рис. 4.П. Программирование таких процедур сводится к организации нескольких циклов с переменными пределами.

г 4

Рис. 4Л1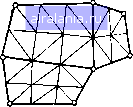

Рис. 4.12

Однако для практических приложений больший интерес представляют универсальные программы автоматического разбиения областей различной сложной формы. В литературе предложены различные способы описания геометрии и алгоритмы дискретизации областей для МКЭ. Наибольшее распространение получил следующий подход. Область сложной формы разбивается вручную на подобласти, которые называются «макроэлементами». Эти подобласти должны достаточно хорошо описывать геометрию расчетной области. Обычно макроэлементы выбирают в форме треугольников п выпуклых четырехугольников, но иногда используют и подобласти, ограниченные кривыми второго порядка. Число таких макроэлементов обычно невелико (несколько единиц или десятков для сложных областей), и поэтому это разбиение можно описать путем задания координат узлов макроэлементов и некоторой условной нумерации макроэлементов и их узлов.

Затем реализуется автоматическое разбиение каждого из макроэлементов на элементарные треугольные элементы. Для этого в исходных данных лишь указывают параметры, характеризующие густоту сетки в каждом из макроэлементов.

Приведем два примера автоматизации разбиения. В первом используются макроэлементы в виде выпуклых четырехугольников (рис. 4.12). Для каждого макрочетырехугольника задается следующая информация: номера узлов в вершинах и признаки принадлежности сторон границе, числа дроблений на отрезки по двУ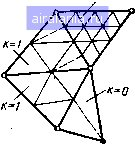

Рис. 4.13

jKHbiM сторонам, массивы кэординат вершин четырехугольников. Каждый из макрочетырехугольников автоматически разбивается маленькие четырехугольники прямыми, проходящими через точки разбиения противоположных сторон на равные отрезки. По-[учеиные четырехугольники в свою очередь ра.збиваются короткими диагоналями на элементарные треугольники. В результате число треугольников в каждом макроэлементе равно 2 kk-i, где А,, - числа отрезков на смежных сторонах. Заметим, что при тако.м способе для общих сторон макроэлементов должна задаваться одинаковая кратность дробления.

Другой способ автоматизации разбиения иллюстрирует рис. 4.13. Здесь в качестве макроэлементов взяты треугольники. Информация о них задается почти в таком же виде, как и для «элементарных» треугольников: массивы координат вершин и индексная матрица, но с одним отличием. В строке индексной матрицы для каждого макроэлемента содержится еще одио число - кратность дробления k. Если k ~~- О, то макроэлемент не дробится и принимается в качестве конечного элемента. При k ---- 1 путем соед1шения центров сторон проводится ра.збиение макроэлемента иа четыре подобных треугольника (рис. 4.13). Прн к - 1 каждый из полученных четырех треугольников еще раз разбивается иа четыре подобных и т. д., т. е. число полученных из макроэлемента треугольников равно 4. Крэтность дробления соседних макроэлементов может различаться не более чем на единицу. При этом, чтобы избежать появления «лишних» узлов на стороне треугольника с меньшей кратностью дробления автоматически проводится построение еще нескольких треугольников. Для Этого узел, лежащий на стороне треугольника, соединяется с противоположной вершиной, как это показано на рис. 4.13 пунктирными линиями. Достоинством данного способа разбиения является Возможность резко сгущать сетку в областях с большими градиентами температур, используя при этом сравнительно небольшое чис-Jo макроэлементов.

Приведенные на «словесном» уровне описания методик автоматического разбиения двумерной области могут создать впечатление •5 простоте их программной реализации. Однако на самом деле про-"раммное «воплощение» этих алгоритмов требует довольно значительных усилии.

В процессе автоматического разбиения области проводится и ну-рация получившихся элементов разбиения. После этого возника- задача оптимальной перенумерации узлов с целью уменьшения "Ширины леиты матрицы. В областях, имеющих форму, близкую к

прямоугольной, нумерацию узлов целесообразно проводить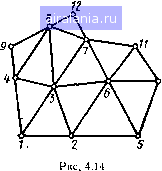

следовательно вдоль направлении, параллельных короткой роне н содержащих меньшее число узлов. В данном случае с° туация аналогична той, что была рассмотрена ранее (см. применительно к решению двумерной задачи методом конечны разностей.

В некоторых программах нумерацию проводят последовательн в пределах каждого макроэлемента в порядке их обхода. При этом в треугольниках, лежащих у границ макроэлементов, могут возни кать большие разности номеров узлов. Можно предложить и другие подходы. Например, хорошо зарекомендовал себя для решения многих практических задач следующей эвристический способ перенумерации узлов. Узел с номером J выбирают где-либо иа границе области. Номера 2, 3 и т. д. присваивают узлам, которые соединены с узлом номер ] сто-10 роной элементарного треугольника (рис. 4.14). После того, как пронумерованы все узлы, соединяющиеся с узлом номер /, в качестве «опорного» берется узел номер 2 н продолжается нумерация узлов, соедниеииых с ним н не пронумерованных ранее. Подобная процедура последовательной нумерации улов, соединенных с наименьшим из ранее присвоенных номеров, продолжается до полной нумерации всех узлов сеткн. После такой перенумерации подсчитывается получившаяся ширина ленты матрицы, которая также является выходным параметром программы разбиения и перенумерации. Поскольку программная реализация описанных автоматических процедур довольно сложна, примеры соответствующих подпрограмм здесь не приводятся.

Формирование глобальных матрицы и вектор-столбца. Перейдем к рассмотрению реализации алгоритмов формирования глобальных матрицы и вектор-столбца. Обычно они строятся на основе методики, изложенной в предыдущем параграфе. В этом случае оформляется подпрограмма для расчета локальных матриц и столбцов.

Входными данными для иее являются координаты узловых точек, передаваемые в соответствии с локальной нумера[(иси узлов, информация о сторонах элемента, лежащих иа границе области, и значения параметров К., q,, q, а. Последние могут вычисляться с помощью специальных подпрограмм, в которых входными параметрами являются координаты узлов элемента, а выходными - значения Х, q, а для этого элемента. В при-

водимом ниже примере (рис. 4.15) предусмотрено использование двух таких подпрограмм: для расчета Х, Ху, (подпрограмма AAA)

q (подпрограмма ВВВ): Обращения к этим подпрограммам имеют вид:

CALL ААА(ХС, YC, АХ, AY, QV) н CALL ВВВ(ХС, YC, ALF, QS).

Эти подпрограммы должны составляться пользователем для конкретной задачи. При формированнн матрицы происходит обращение к ,щм с текущими координатами ХС, УС центра элемента (для AAA) или центра стороны элемента (для ВВВ). Прием, аналогичный описанному, использовался в главе 3 прн решении одномерной задачи теплопроводности методом конечных разностей. Напомним, что при выводе уравнений МКЭ мы считали свойства и мощности постоянными в пределах элемента, поэтому в случае разрывных функций желательно, чтобы лиинн разрыва совпадали с границами элементов.

Входными данными для подпрограммы формирования глобальных матрицы и столбца, приведенной на рис. 4.15, являются: N -число треугольных элементов, М - число узлов, MS - шнрниа ленты матрицы, X, У - массивы координат узлов х, Ут длиной М, 1ND - индексная матрица - массив длиной 4*N. Все эти данные получаются в результате выполнения процедуры разбиения н перенумерации узлов.

В нидекс1юй матрице для каждого треугольного элемента {п Л) записываются четыре целых числа. Первые три числа соответствуют глобальным номерам г, /, k узлов данного треугольника, записанным в порядке обхода против часовой стрелки, начиная с любой вершины. Четвертое число - это признак, с помощью которого задается внешняя граница области. Напомним, что согласно принятому нами способу этот признак принимает значения: О - если ни одна из сторон треугольника не принадлежит границе, 1 - если граничной является сторона между узлами i и /, 2 - если граничной являются две стороны между узлами t и / н между узлами / и к. Другие ситуации с расположением граничных сторон можно исключить соответствующим выбором порядка записи номеров (, /, к.

В приводимой подпрограмме из-за малой размерности локальных матрицы и столбца для расчета их коэффициентов ие используется специальная подпрограмма, а они вычисляются непосредственно в Ней по формулам (4.29), (4.30) (операторы 83-122).

В подпрограмме производятся следующие процедуры. Сначала обнуляются массивы G н F, соответствующие глобальным матрице Столбцу. Далее организуется цикл по всем элементам, в ко-1"ором: