Тепловые потоки {х„ + Ш2) и Q"" {х„ - h/2) аппроксимируются так же, как и в случае одномерного уравнения теплопроводности, см. (3.44):

"""" Qx,h/2)l ".-х-п

Для аппроксимации {х„ + h/2) и Q*" {х„ ложить несколько вариантов:

h/2) можно пред-

Q(x + h/2)riivun+i, Qix-h/jcpvu, (5.6) (х„ + h/2) cpv (Un+i + Un)/2,

(Xn - h/2) cpv(u-Un-i)!2, (5.7)

Q*(x, \-h/2)cpvUn, Q(xn - h/2)cpvun-. (5.8)

Проанализируем соотношения (5.6) - (5.8), учитывая, что жидкость течет в направлении оси х, проходя через элементарные объемы в порядке возрастания их номеров.

В аппроксимации (5.6) принято, что температура втекающей в объем Vn жидкости равна температуре центра этого элементарного объема, а температура вытекающей - температуре центра следующего за ним по течению объема Это приближение является весьма неудачным, поскольку получается, что иа тепловой режим элементарной ячейки V„ не оказывает никакого «конвективного» влияния температура жидкости в предшествующем ей объеме V„ i, но воздействует температура следующего объема Vn+i- Однако физика процесса конвективного переноса такова, что температура жидкости в объеме Vn должна определяться только условиями ее протекания и теплообмена в предшествующих объемах, т. е. жидкость при течении собирает и несет дальше информацию о своем прошлом, но не знает о своем «будущем». Формулы же (5.6) противоречат этому факту, н поэтому их использование приводит во многих случаях к абсурдным результатам расчетов.

При использовании формул (5.7) принимается, что в элементарный объем Vn втекает жидкость с температурой, равной полусумме температур данного и предыдущего объемов, а вытекает жидкость с температурой, равной полусумме температур данного Vn и следующего за ним по течению объема Vn+i. Принципиальных возражений против аппроксимации вида (5.7) нет. Однако следует ожидать, что она будет «плохо работать» при больших скоростях течения. кое свойство схемы можно объяснить следующим образом. Зафнкс руем температуры и„ и u+i в точках с координатами Хп и n+i рассмотрим, как будет изменяться профиль температуры жидкое

Рис. 5.1

между этими точками при увеличении скорости ее движения. Перестройка профиля, как показано иа рис. 5.3, будет приводить к уменьшению изменения температуры на большей части участка 1х„. Xn+i\ и стремлению ее к значению и„. Этот факт следует как из физических соображений, так и из формулы для соответствующего точного решения уравнения (5.3) иа участке U„, х+Ь

u(x)=Un-\-(Un+i - u)

exp(Peh{x~Xn)/h) - l ехр (Рел) -I

(5.9)

г, Cpvfl

где Нед = - так называемое сеточное число Пекле, характеризующее соотношение между конвективным переносом н теплопроводностью на участке длиной h.

Из формулы (5.9) и рис. 5.2 следует, что при больших сеточных числах Пекле, которые соответствуют большим скоростям течения у, целесообразно считать, что через левую границу элементарного объема протекает жидкость с температурой Un-i предшествующего объема а через

правую - жидкость с температурой данного элементарного объема. Сформулированному требованию как раз и удовлетворяет третья аппроксимация вида (5.8). Из приведенных соображений следует, что эта аппроксимация должна хорошо работать при больших скоростях течения.

Формулы (5.6) - (5.8) можно трактовать и так. При использовании (5.6) производная дТ/дх в (5.3) аппроксимируется разностью вперед по направлению движения жидкости (разностью «по потоку»)

дТ Un+1 - Un дх h

в случае (5.7) - центральной разностью: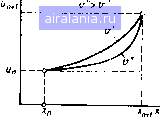

Рас. 5.2

дх 2h

3 В случае (5.8) - разностью назад или разностью «против потока»:

дТ и,,-и.

4t - Чп~1

jj Риваденные рассуждения носили качественный характер. Для Роведеиия более подробного анализа и сопоставления разных видов чроксимации конвективного члена в уравнении (5.3) применим "Дику, использованную нами в §3.3 для исследования коиечио-

разностных схем для уравнения теплопроводности. Запишем приб лнженное выражение для конвективного члена в виде

обобщающем формулы (5.6) - (5.8). Тогда с учетом (5.4) н (5.5) ко-иечно-разностное уравнение для (5.3) записывается так;

cpv (Й1 + a-i Un + из = X ("гц-i - + Un-i}/h

2л \

- acpv

hi -1-1

(5.11)

Как и в § 3.3, будем использовать следующий критерий пригодности разностной схемы для расчетов: при любых ситуациях она не должна давать численных решений, противоречащих физическому смыслу. Рассмотрим с этих позиций две «перспективные» аппроксимации: центральной разностью н разностью против потока.

Для аппроксимации центральной разностью в (5.10) следует положить Й! --= l/2/i, а.2 О, Из - l/2/i. Подставляя этн значения коэффициентов в (5.11), получаем разностную схему

(5.12)

2 АХ

Теперь предположим, что температура жидкости монотонно возрастает по длине канала н > u„ i. Тогда температура «„ должна лежать между н Однако из уравнения (5.12) следует, что при большой скорости V температура может «упасть» ниже значения В частности, если 100, u+i = 102, то прн

h \, Х/ср =-1, 1! - 4 нз уравнения (5.12) получаем и„ = 99. Чюбы не произошло такого чрезмерного падения необходимо выполнить условие

-.„,,-.„ И< нлн-£<2. (5.13)

Таким обра.зом, соотношение (5.13) определяет максимальное значение скорости, для которого .можно проводить расчет ярн данном шаге по пространственной координате. Еслн скорость будет превы шать это значение, то в численном решении может возникнуть, иа пример, немонотонность в распределении температуры.

Приведем пример «плохого» поведения численного решения, лученного при нспользованни аппроксимации центральной Р стью при малых скоростях. В § 5.3 будет рассматриваться Р уравнения энергии для жидкости, находящейся в теплообмене стенкой канала, имеющей постоянную температуру Tw, Д-

когда «теплопроводным» членом в уравиеиии энергии можно Пренебречь по сравнению с конвективным, а изменение энтальпии (щкости обусловлено только ее теплообменом со стенкой:

(5.14)

где сс - коэффициент теплоотдачи; / ~ периметр; 5 - площадь фечного сечения канала.

Конечно-разностная схема прн применеинн центральной раз-

„,.11 UUPpiT RHTT

достн имеет вид

2afh

{Tw - u},

2afh

(5.15)

cpvS "" cpvS

Если температура жидкости на входе в канал меньше Г*-, то по длине канала происходит ее монотонное возрастание, при котором Гстремится в пределе к Гр (рис. 5.3). Прн расчете же по схеме (5.15) при достаточно большом TJ, которое получается прн малых скоростях или больших шагах по пространственной координате, наблюдается следующее явление. Прн подходе численного решения достаточно близко к Tip на каком-то его шаге происходит «перескок» за значение Т--, т. е. температура жнд-ьости превышает температуру стен-и. Поскольку разность (Гц? - "n+i)B (5.15) сразу становится отрицательной, то далее разностное решение снова падает ниже уров-Таким образом наблюдаются колебания, противоречащие зрактеру физического процесса.

1азобранные примеры указывают на то, что аппроксимацию чтральной разностью нужно использовать с известной осторожностью.

Ко PfA К рассмотрению аппроксимации разностью назад, (5,Рой соответствуют коэффициентый! = О, l i, Ид = 1 ib )- Разност:1ая схема (5.11) принимает вид

] I cpvh

Рнс. 5.3

и„ =

TajQ (5.16) видно, что для рассмотренного выше .монотонно возрас-%D° По длине распределения температуры прн любых значениях ростн температура «„ всегда располагается между Un., и Un-i-

cpvhjX

X {2 + cpvhlX)

н-г-

(5.16)

2217

при больших скоростях и„ приближается к u„ i, что согласуется с точным решением {5.9). Для задачи (5.14) при аппроксимации конвективного члена разностью против потока получаем конечно-раз, ностную схему

""~--={Г«-а„)

Un =--. Ц

2afh cpvS

(5.17)

Очевидно, что при расчете по формуле (5.17) при любом значении ц всегда будет выполнено неравенство ц„ < Tw-

Отмеченные положите-тьные свойства конечно-разностных схем, получающихся при использовании аппроксимации конвективных членов разностью против потока, обусловливают их широкое применение. Поэтому именно эта аппроксимация была выбрана нри решении рассматриваемых в § 5.2 и 5.3 задач.

Мы рассмотрели конечно-разностные схемы для решения стационарного уравнения энергии. В случае нестационарной задачи построение соответствующих схем производится на основе приведенных аппроксимаций конвективного и кондуктивного потоков точно так же, как это делалось для на:тацнонарного уравнения теплопроводности, т. е. можно использовать явную илн неявную схемы. В явной схеме потоки берут с предыдущего шага, в неявной - с текущего. Можно ввести и схему с весами. Отмеченные выше отрицательные и положительные свойства аппроксимаций (5.6)-(5.8) проявляются и при решении нестационарных задач. В частности, даже неявная схема с разностью вперед является неустойчивой при любом соотношении шагов по пространственной и временной пере менным. С другой стороны, неявная схема с аппроксимацией разностью против потока безусловно устойчива.

Проведенный анализ различных разностных схем носил в большей степени качественный, чем количественный характер- С йХ строгим теоретическим анализом можно ознакомиться по книгам (21, 23, 241

Перейдем к рассмотрению алгоритмов чнс1енного расчета дву задач конвективного теплообмена, основанных на решении уравнения энергии.

§ S.2. РАСЧЕТ СТАЦИОНАРНОГО ДВУМЕРНОГО ТЕМПЕРАТУРНОГО ПОЛЯ ПРИ ТЕЧЕНИИ В ТРУ&Е

В качестве примера численного решения задачи конвективно теплообмена при заданном поле скоростей рассмотрим задачу чета двумерного температурного поля несжимаемой жиД Т (г, г), протекающей в трубе радиусом R и длиной / (рис, 5.4).

ратур жидкости иа входе в трубу постоянна по поперечному се-jo и равна Т. На внутренней поверхности трубы задано либо

,0ределение по длине температуры стенки Tw (2), либо плотно-L-H теплового потока <?Щ7 (г). Течение считается гидродинамически j-габилнзированиым, т. е. поперечная составляющая скорости Vr - О, 3 продольная Vz (г) ие изменяется по длине трубы. Напри-jiep, Д** ламинарного стабнлизиро-зайного течения профиль скорости длеет параболича:кий внд 1311:

(г) = Ов (1 ~rVR = 2(1 ~ r/R),

(5.18)

где Id " скорость на оси трубы; v - средняя по сечению скорость.

Предполагается, что теплофнзнче-ские свойства жидкости не зависят от температуры и что диссипация энергии за счет вязкого трения й работа сил давления пренебрежимо малы. Тогда стационарное уравнение энергии, описывающее распределение температуры в потоке жидкости, имеет вид

У (г)

Рнс, 5.4

дТ дг

(5-19)

При решении многих практических задач переносом теплоты вдоль трубы (по направлению z) путем теплопроводности можно пренебречь по сравнению с конвективным переносом. Это допущение правомерно прн числах Пекле Pt = vd/a >> 1. Уравнение энергии в этом случае имеет вид

X д

дТ \

(5.20)

дг г дг \ дт ТРичные условия для уравнения (5.20) записываются следую-рии* трубы должно выполняться условие симмет-

дТ дг

= 0,

лнке (г = R) задается либо распределение температуры

распределение плотности теплового потока

дТ . .

qw (2),

(5.21)

(5.22)

(5.23)

входном сечеиии z = О задается температура входящего пото-

Т(г, г)г=о = Г„.

(5.24)