

|
|
Главная -> Применение эвм 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 [27] 28 29 30 31 32 33 и жидкостью учитывается путем задания локального коэффициец та теплоотдачи а, который может зависеть от координаты х, расх?>, да G, температуры стенки Tw и температуры жидкости Tf. Темпера, туриые поля стенки и жидкости считаются стационарными и одцу  O-o-o-o~-o-o- b--о-о--о-о-Ь и, U; Un-"U, Рис. 5.7 Ркс. 5.8 мерными. Распределение температуры стенки Tw {х) описывается уравнением для стержня с боковым теплообменом [51: ?.w Sv,-7 -qi{x)-~afiTw-Tf)0, (5.36) a для температурного поля жидкости Tf {х) рассматривается одномерное уравнение вида af(T При формулировании граничных условий будем считать, что на торцах стеики к средам с температурами Гц. Т( с помощью тепловых проводнмостей oq, <J[ задаются тепловые потоки, т. е. Г -1 - -1- Ai = 0. x-O.I a на входе в канал задана температура жидкости (5.38) (5.39) Для построения разностной схемы введем равномерную пространственную сетку х„ = (л - 1) Л, п = ], N, h = / /(Л" - О (рис. 5.8). В узлах сеткн будем искать две сеточные функции и Un, соответствующие приближенным значениям температур стенки Tw ix„) и жидкости Tj (х„). Разностная аппроксимация для урзВ" иения вида (5.36) и граничных условий (5.38) подробно рассматривалась в § 3.3. При аппроксимации уравнения (5.37) заменим производную разностью «против потока», В результате получим а1едую-щую разностную схему: для граничной точки стеики п = 1 Аз/2 5г %{h ~T-~Ui-o,fih~-i,% (5.40) для внутренних точек стеики п - 2 , N - ! \Хп~ \ /2 {tn+\ - in)--п- 1 /2 (r - In -i)l 4 -a„/(/„ - «„)-0, для граничной точки стеики п = N 1 с -V ~ А - 1 лл-1/2->а -- + at(v-r,)- (5.41) = -~[i?.v - ал/(г,¥- "л(). для внутренних точек жидкости п - 2, N Un - и. для первой точки жидкости п = 1 и, Т„, (5.42) (5.43) (5.44) в формулах (5.40) - (5.43) использованы обозначения = qi {nr - CC (X„, G. tn, M„), K±\/2 U ((±1 + .).2). Записанные разностные уравнения образуют систему 2N алгебраических уравнений относитетьио температур Ип = 1,...,Л). Эта система является нелинейной, так как тештопроводиостн коэффициенты теплоотдачи а„ и мощности на единицу длины qn в нашем случае зависят от температуры. Для решения нелинейной системы используем наиболее простой прием: построим итерационный процесс, иа каждом шаге которого коэффициенты Ki--ifi, Яп рассчитываются по значениям температур tn , Мп на предыдущей итерации, а затем рец]ается система линеаризованных уравнений относительно температур 1п\ и на новой s-й итерации с помощью стандартной подпрограммы. На рис. 5.9 приведен текст программы для реп1ения задачи (5.36) - (5.39). Эта программа оформлена в виде подпрограммы н не содержит операторов ввода-вывода. Исходные данные и результаты расчета являются ее формальными параметрами и их описание дано в комментариях к тексту. Исходными данными служат параметры, входящие в постановку задачи (5.36) -- (5.39), причем предполагайся, Что теплопроводность стенки может зависеть от температуры: tt = ?.w {Т\х>), а локальный коэффициент теплоотдачи - от *сюрдинаты, расхода G, температур стенки Tw и жидкости Т,: а == а (х, G, Tw, Tf). Эти функциональные зависимости описываются в подпрограммах-функциях с именами ALAM. и ALF, кого-
ПРОГРАММА ЧИСЛЕННОГО РЕШЕНИЯ СИСТЕМЫ ОДНОМЕРНЫХ УРАВНЕНИЙ ДЛЯ СТЕНКИ И ПОТОКА ЖИДКОСТИ В КАНАЛЕ SUBROUTINE CANAL «(DL.SW,F,CP.G.S0.SL.T0.TL.UBX. .AUM.ALF.QL.T.U.NN.EPS.lTM.A.Bl ВХОДНЫЕ ПАРАМЕТРЫ: DL - ДЛИНА КАНАЛА SW - ПЛОЩАДЬ СЕЧЕНИЯ СТЕНКИ F - ОМЫВАЕМЫЙ ПЕРИМЕТР СР - УДЕЛЬНАЯ ТЕПЛОЕМКОСТЬ ЖИДКОСТИ G - МАССОВЫЙ РАСХОД S0 - ТЕПЛОВАЯ ПРОВОДИМОСТЬ НА ТОРЦЕ Х=0 SL - ТЕПЛОВАЯ ПРОВОДИМОСТЬ НА ТОРЦЕ X=L Т0 - ТЕМПЕРАТУРА СРЕДЫ У ТОРЦА Х=0 TL - ТЕМПЕРАТУРА СРЕДЫ У ТОРЦА X=L ивХ - ТЕМПЕРАТУРА ЖИДКОСТИ НА ВХОДЕ ALAM - ИМЯ ПОДПРОГРАММЫ-ФУНКЦИИ ТЕПЛОПРОВОДНОСТИ ALF - ИМЯ ПОДПРОГРАММЫ-ФУНКЦИИ КОЭФФИЦИЕНТА ТЕПЛООТДАЧИ QL - ИМЯ ПОДПРОГРАММЫ-ФУНКЦИИ РАСПРЕДЕЛЕНИЯ МОЕШОСТИ T(NN) - МАССИВ НАЧАЛЬНЫХ ТЕМПЕРАТУР СТЕНКИ шт - МАССИВ НАЧАЛЬНЫХ ТЕМПЕРАТУР ЖИДКОСТИ ( ЗАДАЮТСЯ ПРИ РЕШЕНИЙ НЕЛИНЕЙНОЙ ЗАДАЧИ NN - ЧИСЛО УЗЛОВ СЕТКИ EPS - ДОПУСТИМАЯ АБСОЛЮТНАЯ ПОГРЕЕШОСТЬ Ш - МАКСИМАЛЬНОЕ ЧИСЛО ИТЕРАЦИЙ РАБОЧИЕ МАССИВЫ: A(10<.N) - ДЛЯ ХРАНЕНИЯ ЛЕНТЫ МАТРИШ B(2«N) - ДЛЯ ХРАНЕНИЯ ВЕКТОРА-СТОЛБЦА ШХОДНЫЕ ПАРАМЕТРЫ; T(NN) - МАССИВ ТЕМПЕРАТУР СТЕНКИ U(NN) - МАССИВ ТЕМПЕРАТУР ЖИДКОСТИ DIMENSION T(1).U(1).A(1).B(1) 1. ВЫЧИСЛЕНИЕ ПОСТОЯННЫХ ВЕЛИЧИН m=NN-l KMAX=(NN-2)#10+I4 fi=DL/NI Rl=F«f!«fi/SW R2=fi.H/SW R3=F#fi/(CP«G) R4=S0«fi/SW R5=SL«fi/SW R6=R4«T0 R7-R5»TL 1T=I НАЧАЛО ИТЕРАЦИОННОГО ЦИКЛА 2. ОЧИСТКА МАТВЩЫ А 1 DO 2 К=1.КМАХ 2 А(К)=0. 3. ФОРМИРОВАНИЕ МАТВЩЫ А И ВЕКТОРА В Рис. 5.9
Р[1г, 5.9. П[1оло.1женне 197 С ПРИСУЩЕ тШ ЭКАЧО«И ТЕЭвБРАТУР Ш 1»5К=1.(Ш не M(=ABS(T(K)-B{2»N-n> III AF-ABS{U(K)-B(2»S)) иг шли.err.DT) DT=A* ИЗ IFCAF.OT.OT) irr=Af 114 T(H)(2#H-i) 115 5 U(H){2rf) 116 С пкжотсА устш m тютшзст И7 IFdrr.LE.SyS) SO ТО 6 IIS С пр(жт(А УСД0Н1Я no числу wrma 119 1Р(1Т.(Ж.Ш) GO тс ? 12в ГТ=ГТ+1 121 GO ТО I 122 6 RETURH 123 М) Рис, 5.9, Продолжение рые ДОЛЖНЫ составляться пользователем. Выходными параметрами являются температуры стенки t„ и жидкости ы„, записанные в массивы Т и и. Программа реализует решение нелинейной системы разностных уравнений (5.40) - (5.44) и организована на основе циклического повторения итераций, на каждой из которых решается линеаризованная система со значениями теплопроводности и коэффициентов теплоотдачи, вычисленными по температурам предыдущей итерации. Начальные приближения температур стенки и жидкости задаются в качестве входных параметров подпрограммы. Основной частью программы является та, в которой производится формирование линейной системы. Формирование матрицы А и столбца свободных членов В производится на основе единой нумерации всех неизвестных температур. Нумерацию можно проводить различным образом. Например, сначала поставить температуры стенки j!], fjv. а за ними расположить температуры жидкости «1, .... Ид/. При этом все неизвестные температуры сводятся в один вектор-столбец длиной 2Л/- {W,n)i\. Однако такой способ нумерации применять нецелесообразно, поскольку он дает слишком широкую ленту матрицы и приводит к увеличению объема требуемой памяти и затрат машинного времени. В этом случае, например, в первое уравнение (5.40) для температуры стенки входит темпе ратура жидкости и,, и поэтому уравнеине линейной системы д неизвестного a,=fj будет содержать также неизвестное Wn+i = т. е. ширина ленты матрицы при данной нумерации оуд равна jV + 1. пьзо- С целью минимизации ширины ленты целесообразно вать другую нумерацию, ири которой температуры стенки и сти входят в-столбец неизвестных {W„) парами: первыми ид, 1 н «1 -=,2, за ними г, -- (Гз, и= и т.д., т. е. ие-цетные элементы равны температурам а четные W2n - .jMnepaTypaM и„. Рассмотрим структуру матрицы линейной сис-1«мы, которая получается при такой нумерации. Эта матрица условно представлена на рис. 5.10, на котором симваточ «х» отмечены отличные от нуля коэффициенты. В первое уравнение (5.40) ддя 1 = fti входят = и «1 = и соответственно отличны от нуля ai3,ai2, а,з. Во второе уравнение (5.44) для «j = входит только W2, и отличен от нуля ago. В третье уравнение системы (см. (5.41) при п = 2) входят /, = W, = Г3, и., W, = Hs, поэтому не равны нулю й,, а., Й34- 35- Наконец, в четвертое уравнение (см. (5.43) при п = 2) входят IN- IN И, = W, и 1 = W и не равны нулю 42. Структура сле- дующих далее нечетных и четных строк (кроме последней и предпоследней) повторяет рассмотренную структуру третьей и четвертой. Предпоследняя и последняя строки получаются из уравнения (5.42) и уравнеиия (5.43) при п = N. Таким образом, ширина ленты матрицы получается равной 5 и не зависит от числа уравнений. Заметим, что, как видно из рнс. 5.10, матрица яв л я етс я несимметрич ной. Для решения данной линейной системы с несимметричной ленточной матрицей испачьзуется стандартная подпрограмма GELB. описанная в главе 1. Особенностью этой подпрограммы является специфическая форма представления матрицы в виде одномерного массива, образованного коэффициентами, лежащими в пределах ленты матрицы и записанными в порядке ее обхода по строкам. Например, коэффициенты матрицы 1, "22 записываются в элементы массива а, а, а, а. Формирование этого одномерного массива производится следующим образом. Сначала весь массив обнуляется, а затем в него заносятся отличные от нуля коэффициенты путем последовательного перебора строк матрицы. Первые две стро-« и последние две строки просматриваются отдельно (см. операторы Ь-65 и 87-100), а строки, соответствующие уравнениям для внут рениих точек стенки и жидкости, перебираются в цикле (операторы ЦьГ Нетрудно увидеть, что номера для коэффициентов матрицы, стоящих в строках уравнений для л-й внутренней точки стенки, адо отсчитывать от номера (rt - 2) 10 -.- 7, поскольку в первых двух ДУк*" енты находятся 7 коэффициентов, а далее в каждой последующей паре строк ~ по 10 коэффициентов. Этим объясняется вид ератора 68, в котором вычисляется номер элемента одномерного ств- 1оторый заносится первый коэффициент строки, соответ-Ующей уравнению для л-й точки стенки. 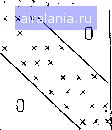 Рнс. 5.10 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 [27] 28 29 30 31 32 33 0.0096 |