вычисления Pf (Г, .... Т/у) на каждом временном шаге решать систему алгебраических уравнений (6.6), в которой собственные лучистые тепловые потоки рассчитываются по известным значениям температур с предыдущего временного слоя. В случае, когда коэффициенты В; не зависят от температуры, коэффициенты матрицы А постоянны для любого временного шага, а изменяются от шага к шагу только векторы свободных членов В, см. (6.7). Поэтому при пе-ализации численной схемы с целью экономии машинного времени целесообразно не решать на каждом шаге по времени систему (6.6), а одни раз перед началом цикла по времени вычислить обратную матрицу D = А", элементы которой обозначим через dtj. Тогда выражения для эффективных потоков примут вид

РФ = ОВ или Pf = 2 diji&jOTj Sf), а для результирующих потоков

/Эре;

V >jiPf-~a,TtSi

N / N \

L/=i Vfei /

(6.10)

Обратная матрица D может быть найдена, например, с использованием стандартной подпрограммы MINV (см. § 1.3). Формирование матрицы А реализовано в приведенной выше подпрограмме (операторы 26-43). При использовании для решения системы (6.9) стандартной программы RKGS, реализующей метод Рунге - Кутта четвертого порядка (см. § 1.5), вычисление правых частей, в том числе расчет РГ согласно (6.10), должно быть реализовано в составленной пользователем подпрограмме.

§ 6.2. РАСЧЕТ УГЛОВЫХ КОЭФФИЦИЕНТОВ. ВЫЧИСЛЕНИЕ КРАТНЫХ ИНТЕГРАЛОВ

Угловой коэффициент излучения [30] между поверхностями Si и вычисляется по формуле

q>i2=

" г cose, cos е., s,dS,, .1 : (6.11) J J

где r - расстояние между элементарными площадками dSi и dSa; 61, 02 - угол между лучом, соединяющим площадки, и нормалями к ним (рис. 6.4). , Таким образом, в общем случае для определения угловых коэф-фициентов необходимо вычислять четырехкратные интегралы (б.И)-Для некоторых видов «взаимодействующих» поверхностей интегри рование можно выполнить аналитически. Получающиеся при это

формулы для угловых коэффициентов приведены в литературе [8,301, Однако для поверхности достаточно сложной формы аналитическое интегрирование часто оказывается невозможным, поэтому прибегают к численному интегрированию.

В главе 2 мы познакомились с методами вычисления одномерных интегралов. При переходе к кратным интегралам возникают новые проблемы, связанные с разбиением области интегрирования и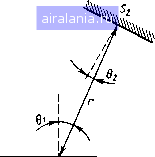

Рис. 6,4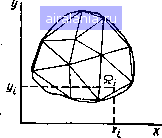

Рис. 6.5

выбором численного метода. Рассмотрим основные методы вычисления кратных интегралов на примере задач расчета угловых коэффициентов.

Область интегрирования для (6.11) такова, что ее разбиение на подобласти можно организовать путем независимого дробления двумерных областей, соответствующих поверхностям Si и S. Поэтому ниже основные методы численного интегрирования будут иллюстрироваться на примере двумерных интегралов.

Метод ячеек. Рассмотрим двукратный интеграл

/ J / (.. У) dxdy

(6.12)

в области Q, представ л еииой на рис. 6.5. При использовании метода ячеек область Q разбивается иа элементарные подобласти и приближенное значение интеграла вычисляется по формуле

Xi, yi) Si,

(6.13)

I 1

*Де Si - площадь г-го элемента разбиения Qj-; х, yt - координаты точки, принадлежащей г-му элементу; - общее число элементов.

Для использования формулы (6.13) необходимо выбрать вид ЗДементов разбиения и положение точки, в которой вычисляется

значение интегрируемой функции, внутри элемента В элементов обычно используют прямоугольники и тпеу е

а точку берут в центре тяжести элемента. При таком попхп""""

ла (6.13) будет точна для линейной

точно разбивается соответствующими элементами"! В случТ"*" вольной дважды иепрерывно дифференцируемой фуикции/Т*" при одинаковом числе п отрезков разбиения по обеим коопдии формула (6.13) имеет второй порядок точности, т. е. ее погпещ убывает пропорционально \/п. пость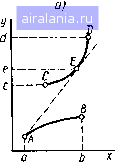

Рис. 6.6

На практике область й часто имеет криволинейную границу, и ее не удается точно разбить иа треугольные или четырехугольные элементы. При этом обычно используются достаточно грубые приближения для граничных слагаемых, и тогда в целом погрешность формулы (6.13) имеет порядок О (1/п).

Если подынтегральная функция имеет лишь первые кусочно-непрерывные производные, то формула (6.13) имеет также погрешность порядка О (1/п).

Сложная форма области и отсутствие непрерывных вторых производных часто встречаются при расчете угловых коэффициентов. Для иллюстрации менее очевидного второго факта рассмотрим расчет флв-CD для плоского случая между кривыми АВ и CD, изображенными на рис. 6.6, а. Этот угловой коэффициент можно представить как интеграл по прямоугольной области, показанной на рис. 6.6, б:

где функция f{x, у) определяется путем проведения соответствующей замены переменных. Остановимся иа особенностях этой фуикции. Зафиксируем какое-либо значение х, например л: = й, и рас-

аптрим поведение фуикции / (а, у) в зависимости от у. Из рис. 56 видно, что на интервале [с, е] значения f {а, у) будут отлич-ы от нуля, а иа интервале [е, d] - равны нулю, так как часть кри-ой ED «не видна» из точки А первой кривой. Поскольку при подходе к точке у = е со стороны меньших значений f (а, у) будет убывать до нуля по косииусоидальиому закону, то в этой точке JJepвaя производная по у будет иметь разрыв.

Рассмотренный пример имеет характерную особенность, обус-;10БЛИвающую некоторые сложности, возникающие прн составлении программ вычисления угловых коэффициентов. Она заключается в наличии у поверхностей взаимной .затененности, которая может быть вызвана кривизной этих поверхностей или наличием в системе других поверхностен. В последнем случае сама подынтегральная функция в (6.II) может иметь разрывы. Из-за затененности для каждой пары элементов разбиения, принадлежащих разным поверхностям, приходится проверять, «видят» ли они друг друга. В многомерном случае реализация такой проверки при наличии многих поверхностей может быть достаточно громоздка.

Метод ячеек непосредственно переносится иа интегралы большего числа измерений. При этом сложности реализации процедуры разбиения для областей сложной формы еще более возрастают по сравнению с двумерным случаем. Поэтому целесообразно проводить замену переменных, обеспечивающую преобразование сложной области интегрирования в многомерный параллелепипед. К сожалению, это ие всегда возможно.

Отметим, что для многомерных областей канонических форм - квадрат, круг, сфера и т.д. - разработаны специальные кубатур-иые формулы вида

где Cl - некоторые коэффициенты; f (х) - значения функций в определенных точках, лежащих в области интегрирования. Коэффициенты d и расположение точек выбираются так, чтобы иа каком-либо классе функций погрешность формулы (6.14) была бы минимальной [2]. Применение подобных формул ограничено требованиями к форме областей.

Последовательное интегрирование. Рассмотрим этот метод иа примере двумерного интеграла по прямоугольнику. Этот интеграл можно представить в виде

/ = j5/(x, y)<xAy==\F{y)Ay,

CO. с

F{y)-\f{x, у)Ах.

(6.15)

(6.16)

прн нспользованнн (6.15), (6.16) сначала с помощью какой-либо квадратурной формулы проводят численное интегрирование по «горизонтальным прямым» и определяют значения функции Р (у) в точках разбиения по переменной у. Затем на основе этих значений также по квадратурной формуле вычисляется окончательное значение двумерного интеграла. В принципе для разных направлений квадратурные формулы могут различаться. Однако обычно используют квадратурные формулы одного порядка точности. Метод последовательного интегрирования можно применять и для областей сложной формы, ио в этом случае при его программной реализации возникают большие по сравнению с методом ячеек сложности.

Метод Монте-Карло. Хотя этот метод целесообразно применять именно для многомерных интегралов и, более того, его эффективность возрастает с увеличением размерности, для простоты сначала рассмотрим основную идею метода на примере одномерного интеграла

Представим этот интеграл в виде

где р {х) - некоторая функция, обладающая свойством

/?(x)dx= 1,

(6.17)

(6.18)

на которую пока никаких дополнительных ограничении не накладываем.

Напомним ряд формул из теории вероятностей. Рассмотрим непрерывную случайную величину X, принимающую значения только из промежутка {а, Ь\ и имеющую функцию плотности распределения вероятности р {х), а также вторую случайную величину Л, связанную с X функциональной зависимостью Л = ф (X). Математическое ожидание величиш.1 X - Е {X} рассчитывается по формуле

Е{Х)=-\хр[х) d.v,

(6.19)

а математическое ожидание Л - 5 {Л} - по формуле

E{h)\-<{x)p{x)dx. (а2С

Сравнивая формулы (6.17) и (6.20), внднм, что интеграл (6.17) можно трактовать как математическое ожидание непрерывной случайной величины Л, связанной с X зависимостью

A-=t(X)

Р(А)

6.21)

Такая трактовка позволяет указать оригинальный способ вычисления интеграла (6.17). Вспомним, что в математической статистике математическое ожидание случайной величины оценивается по среднеарифметическому значению из совокупности результатов ее наблюдений, которые берутся из эксперимента. В методе Монте-Карло применяется такая же оценка, ио результаты наблюдеинй берут не из эксперимента, а получают путем статистического моделирования на ЭВМ. Лля этого реализуется специальная процедура генерирования последовательности значений независимых реализаций X,, .... xn случайной величины X с функцией плотности распределения р (х). Имея набор х,, х, рассчитывают значения X,v реализаций случайной величины Л: Л/ = f{Xi)lp {Xj) и да-дее находят оценку математического ожидания Л по формуле

V \{xi)ip{Xi) 11. (6.22)

Эту оценку считают приближенным значением интеграла (6.17) Процедура получения значении независимых реализаций х,- слу чайной величины X строится на основе стандартных программ для генерации псевдослучайных последовательностей.

Определим погрешность формулы (6.22) для вычисления интеграла. Напомним, что погрешность оценки математического ожидания пропорциональна ее среднему квадратическому отклонению, которое убывает пропорционально Х/Ы. Например, среднее квадра-тическое отклонение а~ выборочного среднего, определенного по выборке >.j, ?.дг нз нормального распределения, равно о- -

= а/уМ, где о - среднее квадратическое отклонение одного результата наблюдения. Для среднего квадрат и чес к ого отклонения оценки (6.22) о~ справедливо аналогичное равенство

(6.23)

Таким образом, погрешность формулы (6.22) можно уменьшать не только за счет увеличения Л, ко н за счет понижения о {Л}. Второй путь можно реализовать специальным выбором функции плотности распределения р (х).

Прн расчете кратных интегралов методом Монте-Карло общая последовательность действий аналогична рассмотренной с единственным изменением: вместо случайной величины X рассматривается