лучайный вектор X. Соответственно при статистическом моделиро-ании каждый раз генерируется не одно знчение xi, а совокупность начений координат случайного вектора X. Обычно это не приво-[ит к существенному усложнению алгоритма, поскольку на практике выбирают функцию р {х) так, чтобы компоненты вектора X мож-ю было считать статистически независимыми. В этом случае любую юординату можно моделировать независимо от остальных анало-ично одномерному случаю.

Остановимся для примера на расчете рассмотренного выше угло-юго коэффициента Флв-сл (см. рис. 6.6) методом Монте-Карло. 3 качестве случайного вектора X здесь выступает совокупность щух значений координат (х, у). Для получения простейшей функции 7Л0ТН0СТИ распределения р (х, у) можно принять, что компоненты с и у статистически независимы и равномерно распределены на соответствующих интервалах своего изменения [а, Ь] и [с, d\:

р{х, )-1/[(Ь-й)(-с)1.

Гогда при вычислении флв-со последовательно генерируются пазы значений координат (xi, yi), для каждой пары рассчитывается значение подынтегральной функции / {xi, yt) и, наконец, после получения реализаций определяется оценка флв-со по формуле

Флл-со= У/(. Уг).

Значения xt, yi генерируются независимо друг от друга с помощью двух обращений к стандартной подпрограмме, рассматриваемой 1алее в § 6.3. При расчете / (Хь yi) остаются все упомянутые выше трудности, обусловленные наличием затененности.

.Мы рассмотрели простейший вариант реализации метода Монте-Карло для расчета интегралов. Существует ряд приемов повышения его точности, с которыми можно познакомиться в [2, 281.

Проведем сопоставление скоростей сходимости методов ячеек и Монте-Карло. Из (6.23) вытекает, что погрешность определения многомерного интеграла с помощью метода Монте-Карло убывает пропорционально MVN, где Л - число многомерных точек. Причем скорость сходимости не зависит от размерности интеграла. В методе ячеек, применяемом для кусочно-аналитических подынтегральных функций, которые, как было указано, часто встречаются при расчете угловых коэффициентов, скорость сходимости пропорциональна Мп, где п - число отрезков разбиения по каждой координате. Поскольку в методе ячеек для расчета т-мерного интеграла необходимо рассчитывать ---= многомерных точек, погрешность численного интегрирования в этом случае будет иметь порядок

liVN. Отсюда вытекает, что для двумерных интегралов (т=2)

оба метода дают одинаковую скорость сходимости, а начиная с трехмерных интегралов скорость сходимости метода Монте-Карло выше. Это позволяет рекомендовать его для численного расчета угловых коэффициентов.

§ 6.3. РАСЧЕТ УГЛОВЫХ КОЭФФИЦИЕНТОВ МЕТОДОМ СТАТИСТИЧЕСКОЙ ИМИТАЦИИ

Основная идея метода. Имитация является одной из разновидностей метода Монте-Карло. Общую идею и схему применения этого метода несколько упрощенно можно сформулировать следующим образом. Для решаемой задачи, котоп-г: lxjctoht в определении некоторого параметра, конструируется случайная величина, распределение которой зависит от этого искомого параметра. С помощью ЭВМ проводится моделирование построенной случайной величины, в результате которого находится набор ее реализаций. Далее по этому набору вычисляется статистическая оценка искомого параметра, которая и принимается за ранение исходной задачи.

В § 6.2 мы разобрали один из вариантов применения метода Монте-Карло, при котором задаче определения интеграла (6.11) ставилась в соответствие случайная величина Л. математическое ожидание которой равнялось искомо.му интегралу. Этот вариант можно назвать статистическим интегрированием. Однако возможны и другие приемы. Ниже мы рассмотрим один из ргаиболее распространенных подходов, основанный на статистической имитации процесса переноса излучения.

Проиллюстрируем его сначала на примере расчета углового коэффициента Ф;;. При подборе подлежащего имитации соответствующего случайного эксперимента надо учитывать в данном случае два обстоятельства. Во-первых, все элементарные площадки dS;, принадлежащие поверхности Si, дают одинаковый вклад в ее общее излучение. Во-вторых, для диффузно излучающей поверхности число фотонов, вылетающих с любой элементарной площадки в направлениях, задаваемых интервалами изменения азимутального угла [т?, + dl и угла отклонения от нормали [9, 9 + dQ] (рис. 6.7), пропорционально произведению cos 9 sin 9 Это вытекает из закона Ламберта

[8, 30], согласно которому интенсивность излучения I рассчитывается по формуле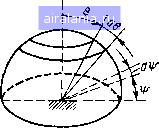

Рнс. 6.7

dQdScose

(6.24)

гдее - полусферическая плотность потока излучения; 0 - угол отклонения от нормали к поверхности; dP - поток, излучаемый а элементарном телесном угле dQ = sin 9d0di:.

Указанные обстоятельства позволяют рассмотреть следующртй случайный эксперимент. На поверхности Sj случайным образом по равномерному распределению выбирается точка. Для этой точка также случайным образом но равномерному распределению для азимутального угла1) и распределению с плотностью вероятности, пропорциональной sin В COS, в, для полярного угла 9 выбирается направление распространения «порции» излучения с энергией Далее рассматривается следующая случайная величина Л: еслв луч, проведенный в выбранном направленик из выбранной точки, попадает иа поверхность Sj, то величина Л принимает значение Q, в противном случае - нулевое значение. Очевидно, что математическое ожидание введенной случайной величины равно

и тогда угловой коэффициент можно определить так;

4>ijBW/Q. (6.25)

Прн проведении статистической имитации иа ЭВМ моделируется случайный эксперимент, по его результатам находится оценка математического ожидания £(Л), а затем нз формулы (6.25) определяется приближенное значение ф;;. Соответствующий алгоритм включает в качестве повторяющегося единичного акта генерацию координат случайной точки иа поверхности S; и значений углов Э И1{}, а также проверку для получившегося направления распространения излучения факта попадания луча на поверхность Sj. Эта проверка похожа на проводимый при расчетах фг по формулам (6.И), (6.13) анализ наличия затенеииости у элементарных площадок. После проведения /V актов испускания излучения оценка математического ожидания Е рассчитывается по формуле

E{A} = nQ/N,

где п - число актов, закончившихся попаданием на поверхность Sj, а приближенное значение ф тогда равно

i,jE{!\}/Q==nlIV. (6.26)

Моделирование случайных величин. Остановимся подробнее на способах генерации случайных координат точки па поверхности Si и случайных углов 9 иф. В основе этих процедур лежит использование стандартных подпрограмм (или подпрограмм-функций), позволяющих получать последовательности псевдослучайных чисел, равномерно распределенных иа интервале [О, П. Например, в программном обеспечении ЕС ЭВМ имеется подпрограмма RANDU (l5i. обращение к которой имеет вид:

CALL RANDU (IX, lY, Z),

где IX - целое случайное число - входной параметр; IY - целое случайное число - выходной параметр; Z - генерируемое подпрограммой веществеииое случайное число нз интервала [0,1].

При первом обращении к подпрограмме входному параметру IX следует присвоить какое-либо нечетное целое значение. При после-дую[цих обращениях входному параметру IX следует присваивать значения выходного параметра IY, полученные при прель1дущем обращении. Часто рекомендуется для уменьшения ки)реляции между ге1{ерируемыми значеииямк Z «прокручивать» датчик несколько раз «вхолостую» перед выбором полученного значения Z в качестве искомого случайного значения.

Отметим, что подпрограммы генерации псевдослучайных после-до1!;1 тельиостей различны дли разных типов ЭВМ (ЕС, СМ ЭВМ, БЭСМ). Это связано с тем, что способы получения псевдослучайных чисел в этих подпрограммах зависят от длины машинного слова (количества двоичных разрядов, отводимых для целых величин).

Очевидно, что если требуется получить случайное значение величины равномерно распределенной на интервале [а, Ь], то с помощью случайного значения Z из интервала [О, 1] это можно сделать следующим образом;

1 Поэтому значение азимутального угла i) из интервала [О, 2п1 оп-[}>еделяется по формуле

-=2л2.

(6.27)

Сложней обстоит дело с выбором случайного значения полярного угла 0, так как его величина должна быть расЕфеделена на интервале Ю, л/2] с функцией плотности распределения вероятности / (6), пропорцнональной sin 9 cos 0, т. е.

/О)-

с sin Э cos 9 при О < О < л/2,

при 6 [О, л/21.

Постоянную с найдем из услорня нормировки функция плотио-распределения вероятности:

(/(6)<iec(sIn«9)/2lJ=l,

да с = 2.

Интегральная фунадия распределения воятности F рШ я в данном случае вероятности попадании зтчшчщ тлпртто ГЛа в интервал (О, 61, имеет вид:

f (0)/(0) de=. sin* 8,

(6.28)

Как было отмечено выше, моделирование иа ЭВМ значений слу. чайных величин с произвольным распределением производится обычно путем специального пересчета значений псевдослучайных чисел, равномерно распределенных иа интервале [0,1]. В основе этого алгоритма часто лежит следующее положение, которое несложно доказать: если имеется случайная величина с интегральной функцией распределения вероятности F (&), то величина z, связанная с соотношением

будет иметь равномерное распределение иа интервале 10, ]]. Так как

f) = f-i(2), (6.29i

то отсюда вытекает, что для получе1ня случайного значения ff можно взять случайное значение z из интервала [0,1] н найти значение из соотношения (6.29). В данном случае

Fe)-sin2e

и случайное значение полярного угла определяется по формуле

e---arcsinV"i. (6.30)

Для выбора случайной точки на поверхности Si, имеющей сложную форму, можно использовать следующий способ. Поверхность Si разбивается иа М элементарных ячеек одинаковой площади Д5. координаты центров которых могут быть вычислены по некоторому правилу. С помощью случайного числа z из интервала [О, П находится целое случайное число k нз последовательности I, 2, по формуле

й = [гУИ]+1. (6.31)

Номер к определяет площадку, из центра которой рассматривается выход луча в направлении, заданном углами и Э.

Программная реализация расчета углового коэффициента. В качестве примера, имеющего чисто учебное значение, рассмотрим программу (рнс. 6.8) расчета методом статистической имитации углового коэффициента сра между двумя бесконечными полосами, расположенными под некоторым углом друг к другу (рис. 6.9)-В данной задаче рассматривается ход лучей только в одной плоскости хОу, т. е. определяется угловой коэффициент между отрезками / и 2. Для упро1цеиия расчетных формул отрезок 1 расположим на оси х между точками хл, хв- Положение отрезка 2 задается двумя парами координат граничных точек {хс. Ус), {хо, Уа)- Для Р

Рис. 6,8