как рассогласование (невязку) между левой и правой частями (1.36), которое возникает при замене и на Р":

Эта величина называется погрешностью аппроксимации исходного дифференциального уравнения разностным уравнением. Из разложения в ряд Тейлора (1.32) нетрудно найти, что

(дТ\ Ат f дТ \ Ат: = - (-

[1.37)

т. е. при достаточно малых Дт погрешность аппроксимации убывает пропорционально первой степени Дт:

[•ф/] < ЙДт, 5 = const или •()/0(Дт).

В этом случае говорят, что разностная схема (1.33) имеет первый порядок аппроксимации. Нетрудно убедиться, что неявная схема Эйлера (1.34) также имеет первый порядок аппроксимации.

Погрешность аппроксимации характеризует различие между уравнениями для точного и для разностного решений- Но малые :и1а-чения еш,е не гарантируют, что сами решения Т/и также будут мало отличаться, т. е. что погрешность е/ будет мала. Возможны ситуации, когда при выполнении условия аппроксимации погрешность численного решения г неограниченно возрастает по мере продвижения по оси т с фиксированным Дт, т. е. при увеличении номера временного слоя /. Для анализа этого вопроса исследуем поведение погрешности численного решения простейшего линейного уравнения теплового баланса

mo Г

.38)

рде то - темп охлаждения [5], а Т имеет смысл перегрева над температурой окружаюш,ей среды. Точное решение задачи имеет вид

Г(т)-Гое-". (1-9)

Разностное решение, найденное по явной схеме Эйлера, можно записать в виде

и/+! = ш (I --то Дт) = и«(1 -то-У\ -"

а по неявной схеме Эйлера - в виде

и/+ I = « (I + то Дт) - uV{l + /По Ат). (1-41)

Точное решение ограничено: Т (т) < То и Т (т->- оо) = 0. Д-*" явной схемы, как следует из (1.40), разностное решение будет огр ничейным только при

1-тоДт<1 или Дт<2/то. (1-42)

Пои -fT > 2/mo разностное решение Ш будет представлять собой илтирующую функцию, амплитуда колебаний которой неогра-"еиио возрастает с увеличением / при движении вдоль оси т. Таким !!\зом, погрешность решения по явной схеме также неограниченно озрастает. Такое явление называется неустойчивостью разностной

схемы.

разностное решение и, наиденное по неявной схеме (1.41), монотонно убывает с увеличением /, и погрешность е=--Т/-иостается ограниченной при любом шаге Дт.

Условие устойчивости разностной схемы для решения задачи (1 29) (1.30) может быть сформулировано в одном из вариантов как требование ограниченности погрешности решения е для любых xj при /

С, С = const.

(1.43)

Более подробно с проблемой устойчивости разностных схем для решения обыкновенных дифференциальных уравнений можно ознакомиться по книге [29].

Таким образом, неявная схема Эйлера устойчива при любых значениях Дт, или безусловно устойчива. Явная схема устойчива лишь при выполнении ограничения на значение шага (1.42), или условно устойчива. При попытках проводить расчеты с шагами Лт, превы-шаюш,ими предельно допустимые из условия устойчивости значения, происходит «раскачка» («разболтка») разностного решения, приводящая к абсурдным числовым результатам или даже к машинному останову из-за переполнения разрядной сетки.

Возникает вопрос, насколько затрудняет проведение расчетов ограничение, накладываемое на шаг Дт в явной схеме. Разумеется при численном решении одного однородного уравнения абсурдно пытаться вести интегрирование с шагом Дт, вдвое превышающим постоянную времени тела. Однако при решении системы уравнений теплового баланса, описывающей нестационарный тепловой режим системы тел с сильно отличающимися постоянными времени, такая ситуация может возникнуть. Если время переходного процесса всей системы определяется телами с большой тепловой инерцией, то может появиться необходимость проводить расчет с шагом Дт, который пре-

шает постоянные времени тел с малой тепловой инерцией. Действительно, если выбрать шаг из условия Дт < 2/ттахт где тах -

ьный из темпов охлаждения отдельных тел, то моает по-реооваться чрезвычайно большое число шагов для расчета зсего тационарного процесса.

(.jJ*OTpeHHbie нами схемы Эйлера имеют первый порядок аппрок-Жеиы / " построения схем с более высоким порядком в разло-W (1-32) нужно оставить члены более высокого порядка малос-

ти по Лт. Например, удерживая члены второго порядка и учитывая что

da г

dT dT V dT

получаем

AxfiTj, и)

dx дт

df dT

дТ dT

IL V

df V

{1-44}

Использование схем, подобных (1.44), затруднено тем, что требуется вычислять производные от функции / {т, Т), и в настоящее время они применяются ие часто. Поэтому возникает необходимость в построении схем с высоким порядком точности, которые не содержали бы производных от / (т, Т). к таким схемам относятся схемы Рунге-Кутта.

Схемы Руиге - Кутта. Для получения схем Рунге-Кутта запишем приращение сеточгюй функции точного решения на промежутке 1т,-, Tj- il в виде

(1.45)

Схемы Эйлера можно трактовать как полученные путем замены интеграла в правой части {1-45) простейшими формулами

h,Hi fij, "О или f{j+, +

Порядок точности разностной схемы можно повысить, если использовать более сложные квадратурные формулы, в которых производная / {т, Т) вычисляется не в одиой, а в нескольких точках отрезка Itj, t; J. При таком подходе возникает задача определения приближений / и соответственно решения и в этих промежуточных точках. Эти приближения вычисляются последовательно по мере продвижения по отрезку [ту, Ту+1 от точки т к точке т-р Так как при этом согласно (1.29) функция/(т, Т) равна производной от решения Т (т), то приближения для решения и строятся на основе оценок значений его производной - значений функции / (т, и). Поэтому в окон-*гательных формулах приближение для / (т, Т) в определенной точке выражается через приближения f (т. Т) в предыдущих точках, сМ. ниже формулы (1.47), (1.48).

Рассмотрим для примера простейшую схему, в которой для вычисления интеграла (1.45) используют две точки: tj и T;+,. Для ее реализации необходимо сначала построить первое приближение значения Т (т) в точке Tjj и. Его находят, используя значения / (ту, «/), по явной формуле Эйлера,

(1.46)

и=«/+Дт(ту, «/).

Подчеркнем, что это первое приближение носит промежуточный ктер. Далее для определения окончательного значения и+ вы-ляют интеграл (1.45) по формуле трапеций с учетом (1.46):

н/+ =ui + At

у/(т>, «о + у/(ту-+1, и)

(1.47)

Нетрудно доказать, что погрешность аппроксимации построенной схемы (1-46), (1.47) равна = О (Дт).

рассмотренная схема являегся простейшей двухэтапнои схемой pyjjj-еКутта. В ней интеграл определяется по двум точкам интервала [т/, ту ,1 и используются два вычисления функции / (т, и) на одном шаге по времени. В общем случае при использовании для определения интеграла Ij, ji гп точек на интервале!ту, Tj-] получается ш-этапная схема Рунге-Кутта. Первая точка для вычисления оценки производной / (т, и) всегда совпадает с ту, а остальные располагаются оптимальным образом с точки зрения обеспечения наивысшего при данном т порядка аппроксимации.

В настоящее время широкое распространение получили четырех-этапные схемы Рунге-Кутта, имеющие четвертый порядок аппроксимации и называемые в связи с этим схемами Рунге-Кутта четвертого порядка. Наиболее употребительная из них имеет вид.

„/+1 = „/ + (д + 2h + 2/з + /4),

(1.48)

Здесь оценки производной вычисляются 4 раза: в точке ту, дважды в точке Tj -j- Дт/2 и в точке т,, а для вычисления интеграла используется квадратурная формула Симпсона.

Схемы Рунге-Кутта (1.47) и (1.48) явные и обладают условной устойчивостью. Например, у схемы четвертого порядка условие устойчивости, проверяемое на модельной задаче (1.38), выполняется только при Дт < 2,8/то.

Рассмотренные два вида схем обладают общей чертой - при определении значения ui+- в узле Xji используется только значение

в предыдущем узле tj. Такие схемы называют одношаговыми. лсно, что в общем случае возможно для определения «+ использовать не только и/, ноии/-\ «/-2 и т. д. В этом случае мы приходим к многошаговым методам, среди которых наибольшее распространение получили линейные.

Линейные многошаговые методы. При построении многошаговых (14к\ в схемах Рунге-Кутта, будем исходить из равенства дпу "" Д-я приближенного вычисления интеграла применим ругой прие.ч, а именно на основе значений функции f (т, и) в k

2 Зак, 2217 33

точках Tj-, Tj- i, Tj--fe i построим интерполяционный полином, kq. торый принимает в этих точках уже известные значения / {tj, «/), .

f {Tj-h+i, u/-*+). Далее, используя продолжение построенного полинома за точку tj {экстраполяцию на отрезок [tj, tji]), можно вычислить интеграл в (1.45), и получить выражение для в котором используются найденные ра. нее значения и,

+ - =

.jj Дт 2 КНу-т+и uf--+% (1.49)

где - постоянные коэффициенты, зависящие от числа точек интерполиции.

Например, если на основе значений ш и «/~ построить линейную функцию {рис. 1.5), продолжить ее иа интервал [tj-. Tj+il н провести интегрирование выражения (1.45), то получим следующую двухшаговую схему: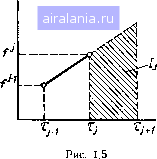

(1.50)

Схемы вида (1.49) явные. Однако несложно получить и неявные схемы. Для этого следует использовать полином, проходящий не только через известные точки Ш, «/-*+\ но и через неизвестную точку «/+. Тогда, интегрируя, получим уравнение неявной схемы относительно «/+

(1.51;

Достаточно часто применяют следующую явную схему при k = 4:

„/4i „/ = [55 --59 ~i+37 -2 9 -3, (j.52)

и неявную при k = 3

(1.53)

здесь = / {tj, ui).

При получении схем (1.49), (1.51) мы исходили из соотношения (1.45). Если же брать за основу равенство

J /(т, u)d%, 0</г<А -I

(1.54)

можно аналогично получить схему

Таким образом, в общел случае линейную /г-шаговую схему можно записать в виде

2 аи- + Дт 2 «-"+)- (1-55)

т= О

В уравнении (1.55) предполагается, что значение «/+вычисляется на основе известных значений ui, Если в (1.55) ро = О»

70 уравнение разрешается относительно ~ схема явная. Если Ро ™ входит и в левую и в правую части, получается в общем случае нелинейное уравнение относительно «/+, схема - неявная.

Остановимся на ряде особенностей многошаговых (при /г 2) методов по сравнению с одношаговыми {k 1).

За счет введения в разностную схему значений функции / (т, «) в й точках, предшествующих искомой (/ -Ь 1)-й точке, удается повысить порядок аппроксимации. Похожий прием использовался для повышения порядка аппроксимации в методе Рунге-Кутта, но там вычисление значений / (т, и) проводилось в точках интервала [tj, Tj- i]. С точки зрения сокращения затрат машинного времени для одного шага новый способ предпочтительнее, поскольку в схемах Рунге- Кутта вычисленные на промежутке [т;, tJ значения / (т, и) не будут использованы на следующем шаге от ту до т j 2. основные затраты времени связаны с вычислением этих значений. В многошаговом же методе прн вычислении «+ мы не сможем использовать только значение /(t i, u/-*+) в наиболее удаленной точке, участвовавшей в определении значения «/+. Остальные значения функции / в точках Ту, Tj fe 2 можно использовать и при вычислении Однако в целом сопоставление затрат машинного времени нужно проводить, учитывая общее число шагов необходимое для достижения заданной погрешности.

В отличие от одношаговых методов многошаговые не являются са-мостартующимн. Действительно, в одношаговых методах вычисления можно начать с и" = То, получить на его основе «, затем на основе аити «2 и т. д. При использовании же многошаговых методов при > 2 вычисления могут начаться только лишь с и* при условии, что f<aKHM-To образом определены и", и, и*-. Эти стартовые значе-•Ия находят с помощью какого-либо одношагового метода, в качестве •которого обычно используют одну из схем Рунге-Кутта.

С точки зрения ограничения на шаг Дт, связанного с требованием •наличия у схем устойчивости, явные многошаговые методы не имеют преимуществ по сравнению с явными методами Рунге-Кутта. 2*