fib)

Рис. 2.2

установить интервалы, в которых следует искать корни. Дальней задача состоит в сужении интервала, в котором лежит корн; столько, чтобы его ширина ие превышала требуемую iiorpejjj онределеиия корня. .

Нелинейные уравнения решаются с помощью итерационных тодов, т. е. процедура решения заключается в многократном шУ нении иекоторого алгоритма. Полученное решение всегда являр! приближенным, хотя для сходящегося а.тгоритма может быть HacTcJ" ко близко к точному, насколько позволяет используемая в ЭВМ г

тема чисел с плавающей точкой. Рассм рим наиболее употребительные итеп-ционные методы.

Метод половинного деления. Эт>[ метод наиболее прост и позволяет на дежно найти корень в ситуации, когда функции / (р) известно только то. что она непрерывна и меняет знак на интервале !а. Ы. Ои состоит из следующих шагов: 1) вычисляется среднее значение --- {а Ч b)i2\ 2) находится значение функции f {с) в средней точке интервала; 3) если знак f [с) совпадает со знаком / (а), то левая граница интервала а заменяется на с; если совпадают знаки / (t) ц / (/;). то правая граница Ь заменяется на с. и в результате интервал сужается вдвое; 4) если ширина вновь полученного интервала мень-Hie заданной погрешности е, то корень считается найденным, в противном случае делается переход к шагу 1.

Описанную процедуру иллюстрирует рис. 2.2. Прекращать вычисления можно не только по разности {Ь - а), но и 1ю абсолютно.му значению / (с). Но обычно этот способ менее наде жен. Например, в нашем случае (см. рис. 2.1) при корнях, близких к {п - 1)л, величина f (ц) может быть достаточно большой даже при узких интервалах !а. Ь\.

Хотя метод половинного деления может потребовать бшьшй число итераций по сравнению с другими методами, он всегда гарантирует получение искомого решения. Поэтому если вычисление однО го значения / (р) в программе происходит за небольшое время, то можно смело использовать этот метод.

После проведения k итераций ширина первоначального интервала, в котором находится корень, убывает в 2* раз. Так, для нашего ин тервала шириной л/2 1,57 после десяти итераций погрешность BfJ-числения корня будет около 0,0015.

Ниже приводится подпрограмма (см. рис. 2.12) для вычислени* корней уравнения (2.15) по алгоритму половинного деления. ВхоД иыми данными являются число корней jV, погрешность е и число Б а результатом - массив корней {р,,В подпрограмме учтен", что каждый корень р„ лежит в интервале 1(п - 1)л, (2п - 1)я/21 54

поскольку функция / (р) на левой границе интервалов Кроме цaтeльнa, для построения нового интервала достаточно сегДЗ ""Р jjgj f [с): если / (с) < О, то с становится новой левой проверит новой правой. Обратим внимание, что i-paHHUg ,дует задавать . чтобы не слишком приблизить-Qi-реш малых числах Bi и не вызвать переполнения по-

*"при вычислении ctgp. Логическан Pvna программы подробио пояснена в f(M} Сентариях к тексту.

Етифуикция /(р) достаточно гладкая.

0/.-ГП есть возможность значительно со--тп 4aci*j „ ,

оатить количество вычислении функции

сравнению с методом половинного деле-"ия Известны различные итерационные методы из которых мы рассмотрим только метод Ньютона, метод секущих и метод простой итерации.

Метод Ньютона. В § 1.2 метод Ньютона был рассмотрен применительно к системе

двух уравнений специального вида. Он может быть использован и при решении трансцендентных уравнений. В этом случае в его основе лежит разложение функции / (р) в ряд Тейлора в окрестности некоторого приближения к корню р***:

/(p) = f(p0 + /4t*)(H-H*)---

Предполагается, что в этой окрестности функция / (р) хорошо описывается линейным членом разложения и следующее приближение к корню р(*+* находится из условия

Рис. 2.3

отсюда

/(H+*)=/(p*) + /4t*) (p*+*-t) = o,

(2.16,1

Значение pC+i) соответствует точке, в которой касательная к кривой в точке ц(> пересекает ось р (рис. 2.3).

В результате корень уравнения находится как предел последовательности, вычисляемой по формуле (2.16). Можно доказать что / (р) = О, / (р) О, а /" непрерывна, то около корня р существует интервал, при попадании в который начального приближения pW метод сходится. Поэтому основная трудность реализации ода Ньютона состоит в выборе начального приближения р>. -чно этот выбор производится с помощью какого-нибудь безуслов-0 сходящегося алгоритма, который может быть основан, например, а Методе половинного деления. После определения р*> выполняется

Феход на ньютоновские итерации, имеющие более быструю сходимость f .

На рис. 2.4 показано, что для нашей функции [ (р) - (2 15 рации по методу Ньютона всегда сходятся при выборе начально ки левее корня р„, но могут привести к выходу из интервала rin боре р* правее корня. \

Если нахождение производной f (р) в методе Ньютона затруд; то можно воспользоваться его модификацией - методом се.кии В этом алгоритме начинают с двух приближений к корню - .S -,ti) .....----- ------------ ------- ------ "

р(\ Функция f (р) заменяется прямой, проходящей через точ/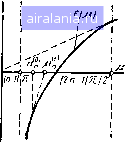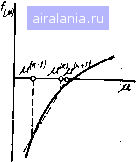

Рис. 2.4

Рис. 2.5

[ (р*"**) И [ (р(>), т. е. вместо касательной в методе Ньютона строится, секущая (рис. 2.5). Тогда по двум приближениям р(*-> и р(*>сле. дующее приближение к корню находится по формуле

[/(и->)-/И>)1/(и<*->-ц<)

(2.П)

в которой по сравнению с формулой (2.16) производная заменена конечной разностью на отрезке [р*"),

Метод простой итерации. В заключен не остановимся на самом простом методе решения нелинейных уравнений, который так и называется - метод простой итерации. Для применения этого метода уравнение (2.14) представляется в виде

р=Ф(р). (2.181

Очевидно, что это всегда можно сделать, если ввести, например

Ф(М) = (М) + М-Итерационная формула метода имеет вид

р(* + 0 =(p(tft)). 2.19

Ясно, что если такой алгоритм сходится, то он сходится к KopHi уравнения. Для сходимости требуется, чтобы в окрестности корня, которой выполняются итерации, соблюдалось неравенство 1ф (р)1

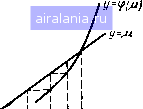Рис. 2.7

\ На рис. 2.6 показан пример сходящегося, а иа рис. 2.7 - расхо-птегося процесса простой итерации.

Отметим, что переход от уравнения (2.14) к уравнению (2.18) моет производиться различными способами и соответственно будут по-Гичаться разные схемы простой итерации. Например, в нашем случае уравнение (2.15) можно представить в виде (2.18) следующими способами:

1) p=Bictgp. ф (р)-Bi/sinV; 2) p = p--p/Bi + ctgp, Ф(М) = 1--\

3) p-i + p/Bi -ctgp, ф(р) = 1 +

Итерационный процесс для варианта 3 будет всегда расходиться» так как ф (р) > 1. Варианты 1 и 2 при некоторых числах Bi в некоторой окрестности точки (2п - 1)л/2 могут давать сходящееся решение.

§ 2.3. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

Задачи вычисления определенных интегралов возникают в расчетах по многим аналитическим решениям. Приведем ряд примеров-

При использовании метода конечных интегральных преобразова. нй [3] приходится вычислять интегралы вида

Де (х), {х) - пространственные распределения объемной и поверхностной плотностей теплового потока; f„ (х) - собственные *РУнкции краевой задачи.

Решения задач с переменными воздействиями (т), (т) -мощью теоремы Дюамеля 1131 представляются в виде

t{x, т)= г7(л:, (уДт-т). gsi---}, т:){1т, о

где i-решение задачи с постоянными юздействиями.

Решения задач в полуограннченном теле с помощью интегра! ного преобразования Фурье представляются в виде несобственны/ интегралов

t(x, у)

в {у, 6>) COS Cd.vdo),

где 6 (у, со) - косинус-преобразование Фурье (изображение) функ, цш[{х,у).

Часто в приведенных интегралах аналитическое выражение длч первообразной найти не удается, дажееслн подынтегральная функции содержит элементарные функции, а во многих решениях под интег ралом встречаются специальные функции (например, функции Бесселя). В этих случаях приходится прибегать к численному интегрированию.

В даниом параграфе рассмотрим методы вычисления одномерных интегралов, а методы вычисления кратных интегралов будут изложены в главе 6 на примере задач нахождения угловых коэффициентов излучения.

Итак, ставится задача приближенного расчета определенного интеграла

1= f{x)6x.

(2.20)

Эти расчеты проводят по так называемым квадратурным формулам, в которые входят значения подынтегральной функции / (х) в конечно\! числе узлов, расположенных на отрезке [а, Ь].

Простейшая из квадратурных формул -формула прямоугольников. При ее построении отрезок интегрирования [а, Ь) разбивается на N элементарных интервалов [ль Xi -i], i = 1, /U, Xi " a, XAf+i = b, и на каждом из них функция [ (х) заменяется постоянным значением (рнс. 2.8)

Тогда на j-M интервале разбиения можно определить приближенное значение интеграла lij+i по формуле

(Xi+i-Xt).

Гуммируя по всем элементарным интервалам при равномерном биении с шагом h = jt+i - л:,-,получаем следующую приближеи-

Рую Wmy-

b - a N

(2.21)

При более общем подходе на отрезке [а, Ь] выбирается (iV + 1) узел {xi)i=\ и приближенную формулу для вычисления интеграла 2 20) записывают в виде

«4-1

1= 1

(2.22)

Задача построения квадратурной формулы состоит в выборе расположения узлов Xi и значений весовых коэффициентов с,-. Довольно часто функция [ (х) бывает задана в табличном виде и поэтому узлы xi оказываются фиксированными.

Рассмотрим общий подход к определению коэффициентов при заданных узлах. Общий интервал интегрирования fa, b] разбивается на совокупность интервалов, ограниченных узловыми точками (рис. 2.9). Хотя в принципе интервалы разбиения могут содержать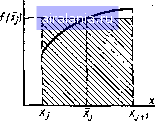

Рис. 2.8

x,-a---Xj Xjt,.,.Xj;-r Xft-tf Рис. 2.9

разное количество узлов, на практике их число делают одинаковым, о /-м интервале разбиения [xj, xj+mh содержащем т + 1 точку, Подынтегральная функция f (х) заменяется интерполяционным полиномом степени т - ф,„ (х), значения которого в узлах Xj, Xji, ...

совпадают со значениями подынтегральной функции. Да-е вычисляют интеграл от интерполяционного полинома по /-му ии-рвалу разбиения:

5!>