Таким образом, святой Георгий настигает дракона в строгом соответствии с условиями и в той элегантной манере, какую мы и могли ожидать от него.

162. Существует много решений этой небольшой сельскохозяйственной задачи. Вариант, который я привел здесь на рисунке, довольно удивителен в том отно-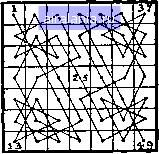

шении, что содержит длинные участки параллельных прямых, образованных ходами.

163. Имеется ряд интересных моментов, связанных с этой задачей. Прежде всего если на положение двух концов пути не накладывается никаких условий, то совершенно невозможно составить такой путь, если только мы

не будем начинать и заканчивать его в верхнем и нижнем рядах конур. Мы можем начинать в верхнем ряду, а заканчивать в нижнем (или, разумеется, наоборот), или же

мы можем начинать в одном из этих рядов и заканчивать в нем же. Но мы не можем начинать или заканчивать путь в одном из двух центральных рядов. Однако начало и конец пути фиксированы условиями задачи. И все же первая половина нашего пути должна целиком ограничиваться теми клетками, которые на рисунке отмечены кружками, тогда как вторая половина пути должна, следовательно, ограничиваться клетками без кружков. Можно заметить, что клетки, обведенные для двух полупутей, расположены симметрично.

Следующий момент состоит в том, что первый полупуть должен заканчиваться в одном из центральных рядов, а второй полупуть обязан начинаться в одном из этих рядов. Теперь это очевидно, поскольку полупути должны быть связаны друг с другом, дабы образовать целый путь, а каждая клетка внешнего ряда связана ходом коня лишь с квадратами своего типа (то есть либо с кружками, либо без кружков). Следовательно, полупути могут соединиться лишь в двух центральных рядах.

Далее: существует 8 различных первых полупутей и соответственно столько же вторых полупутей. Можно заметить, что из них удается составить 12 полных путей, а это и есть число различных правильных решений нашей головоломки. Я не собираюсь их здесь полностью перечислять, однако приведу ответ в такой форме, чтобы читатель сам без труда смог их все найти. Следующие числа соответствуют клеткам рисунка с теми же номерами.

Восемь первых полупутей - это от У до б (2 пути); от / до 5 (1 путь); от / до 10 (3 пути); от 1 до 12 (1 путь) и от 1 до 14 (1 путь). Восемь вторых полупутей: от 7 до 20 (1 путь); от Рдо 20 (1 путь); от 11 до 20 (3 пути); от 13 т 20 (1 путь) и от 15 до 20 (2 пути). Каждый новый способ, каким вы сумеете связать один полупуть с другим, даст новое решение задачи. Можно определить, что эти связи таковы: с 6 на /J (2 случая); с 10 на 13 (3 случая); с 8 на. 11 (3 случая); с 5 на 75 (2 случая); с 12 на 9 (1 случай) и с на 7(1 случай). Следовательно, существует 12 различных способов соединения и соответственно 12 различных решений нашей головоломки. Можно показать, что путь, приведенный на рисунке в условии задачи, состоит из одного из трех полупутей,

идущих от 1 до 10, и полупути от 18 до 20. Стоит отметить, что 10 решений порождены пятью различными путями и их обращениями; другими словами, если вы отметите на рисунке эти 5 путей линиями, а затем перевернете рисунок вверх ногами, то получите 5 новых путей. Остальные два решения симметричны (в этих случаях 12 связано с 9, д. 14 ~ с 7), п, следовательно, не порождают новых решений с помощью поворотов.

164. Изящное симметричное решение этой головоломки показано на рисунке. Каждый из четырех кенгуру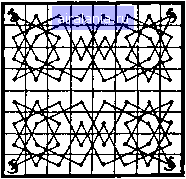

совершает свою небольшую экскурсию и возвращается в свой угол, ни разу не прыгнув в клетку, посещавшуюся другим кенгуру, и не пересекая центральной прямой. Читателю сразу же придет в голову возможность улучшить головоломку, разделив квадрат вертикальной прямой и потребовав, чтобы кенгуру не пересекали также и ее. Это означало бы, что каждый кенгуру ограничен квадратом 4 X 4, но это невозможно, как я покажу в решении следующих двух головоломок.

165. Пытаясь решить эту задачу, сначала необходимо взять два различных отсека соответственно из 20 и 12 клеток и проанализировать, где могут находиться здесь места входа и выхода. В случае большего отсека можно определить, что, желая совершить на нем полное турне, мы должны начать и закончить на двух внешних клетках