162. Пшеничные поля фермера Лоуренса. Одним из самых красивых мест, куда можно летом прогуляться из Лондона, является часть Бекингемшира, известная как Шахматная долина. Правда, с тех пор как ее обнаружил один спекулянт земельными участками, там многое изменилось. В начале нашего века жил в тех краях неподалеку от Лейтимерса богатый, но эксцентричный фермер по имени Лоуренс. У него была любопытная странность; он полагал, будто каждому, кто живет близ берегов Шахматной реки, следует познакомиться с благородной игрой того же названия. Дабы укрепить эту мысль в сознании соседей и домочадцев, фермер порой прибегал к довольно странной терминологии. Например, когда овца приносила ягненка, он говорил что она «провела пешку в ферзи»; когда он ставил новый амбар у дороги, то говорил, что «делает малую рокировку», а когда он посылал человека с ружьем прогнать соседних птиц со своих полей, то называл это «атакой ладей противника». Соседей забавляли эти небольшие шутки фермера, и только один мальчишка (деревенский шут), которому этот пожилой джентльмен однажды надрал уши за воровство «шахматных головоломок», позволил себе предположить, что старик выжил из ума.

7 Генри Э. Дьюдени

Был год, когда Лоуренс засеял пшеницей и рожью большое квадратное поле, разделенное на 49 квадратных участков, как показано на рисунке. Причем сделал это так, что участки, соответствуюшие белым квадратам, были засеяны пшеницей, а черным - рожью. Когда подошло время уборки урожая, он распорядился, чтобы его люди начали с пшеницы на участке 1, а потом всякий раз убирали участок, до которого от последнего убранного участка можно добраться одним ходом коня. Кроме того, тринадцатым по счету следовало убрать участок 13, двадцать пятым - участок 25, тридцать седьмым - участок 37 и последним, сорок девятым, - участок 49. Это было слишком много для его поденщиков, и каждый день фермеру Лоуренсу приходилось самому идти в поле и показывать, какой именно участок следует убирать. Однако эта задача, вероятно, не затруднит моих читателей.

163. Головоломка с борзой. В этой головоломке речь идет о 20 конурах, которые отделены друг от друга низкой стенкой. Единственным их обитателем является борзая, которая живет в левом верхнем углу. Когда ее выпускают погулять, то на свободу она должна выбираться, не иначе как побывав в каждой конуре всего по одному разу и сделав серию ходов коня, чтобы выскочить в правом нижнем углу, где находится выход. Линиями на рисунке показано одно из решений. Головоломка со-

стоит в том, чтобы определить, сколькими различными путями борзая может выбраться из своей конуры наружу.

164. Четыре кенгуру. Сначала я хочу пояснить, что рисунок изображает 64 загона, отделенных друг от друга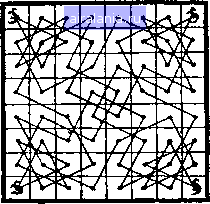

изгородями, которые находятся где-то в Австралии. Я, конечно, далек от того, чтобы утверждать, будто наши родичи «с той половины» всегда разгораживают свои земли столь методичным образом. Можно заметить, что на каждом угловом участке сидит по кенгуру. Я не могу вам объяснить, почему кенгуру имеют пристрастие именно к угловым участкам, но по поводу того, что они всегда прыгают ходом коня, с уверенностью берусь утверждать, что «ход коня» был бы непременно «ходом кенгуру», если бы шахматы не были изобретены задолго до кенгуру.

Так вот головоломка состоит в следуюи1ем. Однажды утром каждый кенгуру отправился на прогулку и, сделав 16 последовательных ходов коня, посетил ровно 15 различных загонов и вернулся в свой угол. Ни один загон не посещался более чем одним кенгуру. На рисунке показано, как им удалось этО сделать. Вам же нужно показать, каким образом они могли бы добиться своей цели, чтобы при этом ни один кенгуру не пересек центральной горизонтальной прямой, разбивающей квадрат на две равных части.

165. Доска, разбитая на отсеки. Нельзя разбить обычную шахматную доску на 4 равных квадратных отсека и