так что достаточно найти лишь одну из половинок, а затем выписать дополнения. Так, в случае ленточки, если вы прибавите 05882352 к 94117647, то получите 99999999; точно так же дело обстоит и с нашим длинным ответом. Обратите также внимание, что на приведенном выше рисунке дополнительными друг к другу являются не только противоположные числа на внешнем кольце, но также и противоположные числа на внутреннем кольце, сумма которых всегда равна 17. Мне стоит, быть может, отметить, что ограничивая наши множители первыми девятью числами, мы, видимо, допускаем возможность, что короткий период может привести к решению с меньшим числом цифр, но есть причины считать это невероятным.

84. Если бы не требовалось, чтобы все квадраты были одинаковых размеров, то ковер можно было бы разрезать на четыре части любым из трех способов, показанных на рисунке. В каждом случае две части, от-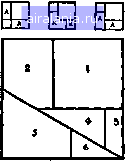

меченные буквой А, если их сложить вместе, образуют один из трех квадратов, два других квадрата состоят из одной части. Но для того, чтобы получить квадраты одинаковых размеров, нам придется разрезать ковер на 6 частей, как показано на большем рисунке. Часть 7 сама является квадратом, из частей 4 и 5 можно сложить следующий квадрат, а из частей 2, 3 и 6 - третий, все одинакового размера.

Если из этих трех квадратов сложить прямоугольник IDBA, то среднее пропорциональное двух сторон прямо-

угольника равно стороне равновеликого квадрата. Продолжите АВ до С, сделав ВС равным BD. Затем поместите ножку циркуля в точку Е (середина AQ н опишите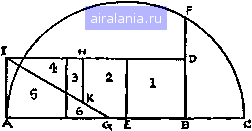

дугу АС. Я показываю совершенно общий метод превращения прямоугольника в квадраты, но в данном частном случае мы, конечно, можем сразу же поместить ножку циркуля в точку Е, которую искать не приходится. Продолжим BD до пересечения с дугой в точке F, и BF окажется искомой стороной квадрата. Далее отметим AG н DH, равные BF, и проведем разрез IG, а также разрез НК из Н перпендикулярно ID. Шесть искомых частей пронумерованы так же, как и на первом рисунке.

Можно заметить, что я сначала привел здесь обратный метод: разрезал три малых квадрата на шесть частей, из которых можно сложить большой квадрат. В случае нашей головоломки мы можем действовать следующим образом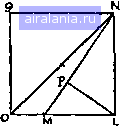

Возьмем LM равным половине диагонали ON. Проведем прямую NM и опустим из L перпендикуляр на NM. Тогда LP будет равно стороне всех трех квадратов, сумма

площадей которых равна площади большого квадрата QNLO. Читатель сможет теперь без труда вырезать шесть искомых частей, пронумерованных на первом рисунке.

85. Читателю может прийти в голову, что история о медведе на Северном полюсе не имеет никакого отношения к изложенной далее головоломке. На самом деле это не так. Одиннадцать медведей невозможно расположить таким образом, чтобы они образовали семь рядов по четыре медведя в каждом. Но другое дело, когда капитан Лонгбау сообщает нам, что «оказалось семь рядов по четыре медведя в каждом». Ибо если расположить их так, как показано на рисунке, чтобы три медведя оказались на одной прямой с Северным полюсом, то на каждой из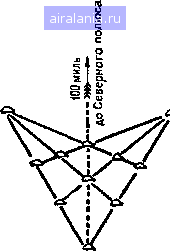

семи прямых действительно будет по четыре животных. На решение задачи не влияет, очевидно, тот факт, имеет ли этот седьмой ряд в длину сотню миль или сотню футов, лишь бы он был прямым - обстоятельство, которое капитан, быть может, проверил с помощью своего карманного компаса.

86. Требовалось показать, как житель города А мог бы посетить каждый город только по одному разу и закон-