

|
|
Главная -> Справочник по алгоритмам 0 1 2 3 4 5 6 7 8 9 10 11 12 [13] 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 операции исполняются от начала до конца - см. пример вычисления площади круга по формуле S=nD/4. Словесный алгоритм при этом следующий. 1. Введем численное значение D и присвоим его переменной DiD-D). 2. Вычислим nDfA и присвоим полученное значение переменной S {5-лО/4). 3. Выведем на печать значение переменной S. 4. Организуем останов ЭВМ. ZBBodD / Вьтисление Стоп Рис. 2.3. Алгоритм вычисления площади круга Соответствующий графический алгоритм показан на рис. 2.3, а, программа имеет вил й5 REMВЫЧИСЛЕНИЕ ПЛОЩАДИ КРУГА 10 INPUTВВЕДИТЕ ДИАМЕТР КРУГИ D=D ге иЕТЗ=#Р1ж112-4 30 PRINTПЛОЩАДЬ КРУГА S=S 40 END Обратите внимание на комментарии при операторах INPUT в строке 10 и PRINT в строке 30. У разветвляющихся программ вычисления производятся в различных частях в зависимости от заданных исходных данных или результатов вычислений. Это обеспечивают операторы условных переходов. На рис. 2.4 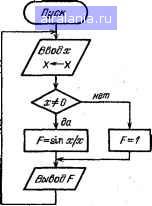 показан графический алгоритм вычисления функции F{x) =sm х/х при хфО и f(;) = l при х = 0. Соответствующая программа приведена выше (в § 2.1) при описании операторов IF...THEN. Циклические программы обеспечивают циклическое (т. е. повторяющееся) выполнение отдельных фрагментов заданное или конечное, но неопределенное число раз - до получения регультата с заданной погрешностью. Циклы с заданным числом повторений организуются с помощью операторов FOR ... ТО ... STEP и NEXT. Примеры правильной и неправильной организации ряда циклов даны на рис. 2.5. -/т 11 ТО N -I-FOR 1=2 ТО М -r-FOfi Л=5 ТО Р - NEXT К- I-NEXT I- -NEXT I-а -FOR 1=1 ТО N ••• -FOR 1=2 ТО М -rFOR Я=3 Р ••• Рис. 2.4. Алгорнт.м вычисления функ11ии sin х/х NEXT I.................... •NEXT J.................... NEXT Н....................... Рис. 2.Ъ. Правильная (и) и неправильная (б) организации циклов с помощью операторов 1-OR и NEXT Пример. Построение циклической программы с циклом, повторяющимся заданное число раз. Пусть надо вычислить А-е число Фибоначчи. Hiiiro.MHn.vi, что числа Фибоначчи образуют носледовательность, у которой каждый очередной член равен сумме двух предыдущих: 0 11 L> 3 5 8 13 21 34 2-(-;i = ,-i r:i-(-2l=34 С-ловесное описание алгоритма может быть следующим. 1. Задаем число N. 2. Присвоим переменной А значение О (.А-1-0), а переменной В значение 1 (В-.-1). 3. Организуем цикл вычислений С = = А--В, организовав счетчик цикла с помощью переменной I, значение которой должно меняться от начального 1 = 3 до конечного I = N с шагом, равным 1. В конце каждого числа проведем замену переменных: АВ и ЪС. 4. При I = N зададим выход из цикла Графический алгоритм вычислений пока-и выведем на индикацию число С. зан на рис. 2.7. 5. Перейдем к выполнению п. 1 с помощью . операции безусловного перехода. С Пуск ) А=0 в=/ \,нет с=а+в а=в в=с ГвыМй I -( Ионеи, } Пуск ) / ВВоВЕ / / Вдовх / 1=7 S=0 Z=S S=S+K/l 1=1+2 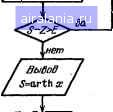 Рис. 2.6. Алгоритм вычисления чисел Фибоначчи Графический алгоритм рещения этой задачи показан на рис. 2.6. Программа имеет вид 18 ШРиТЗАДЙйТЕ N>=3 N=N:LETA=e:LETB= 28 FOR 1=3 ТО N STEP 1 30 LETC=A+BsLETA=sBsLETB=C 40 NEXT I 58 PRINTFN=C:60TO 18!END 60 PRINT!F1.9!FN=C 78 60T0 2e:END В строке 10 организован ввод значения N и присвоение переменным А и В значений О и 1. В строке 20 задан заголовок цикла и указаны пределы изменения (от 3 до N) управляющей переменной 1. Далее в строке 30 проводятся вычисление переменной С = = А + В, присвоение переменной А значения В и переменной В значения С. В строке 40 задан возврат из цикла, если I = N. И, наконец, в строке 50 задается печать значения переменной С и безусловный переход к строке 10. Задав, например, N=10, получим результат 34. Пример. Построение циклической программы с циклом, повторяющимся до получения результата с заданной точностью. Пусть надо вычислить обратный гиперболический тангенс arth х с заданной точностью Е=Е, используя разложение в ряд х зс" х arth л:=х+ + -+ - +..., х<\. Для s-joro будем вычислять сумму членов x/i для /-(-/ + 2 при начальном /=1. Рис. 2.7. Алгоритм вычисления функции arth х разложением ее в ряд В программе (см. с. 46, сверху) цикл организован в строках 30 и 40 с помощью операто-ров IF ... THEN, ведущих сравнение разности (S -Z), где Z - предшествующее значение S, с числом Е, задающим погрешность. Если (S -Z)>E, то организуется условный переход к выполнению строки 30. В противном случае выдается на индикацию или печать результат вычислений (строка 50) и происходит безусловный переход (строка 60) к строке 20, т. е. ввод нового значения аргумента х, и вычислению arth х. Подобным образом строится большинство программ вычисления специальных функций по их разложениям в ряд, вычисления рядов и сложных числовых последовательностей. Следует отметить, что остановка счета в данном случае возможна, если ряд является сходящимся. Обращения к подпрограммам производятся в том случае, когда отдельные фрагменты программ должны выполняться при различных значениях исходных для их вычисления данных. Подпрограммы, как и циклы, могут вкладываться друг в друга (см. рис. 2.8). При завершении выполнения подпрограммы происходит возврат в исходную программу и выполнение оператора, следующего за обращением GOSUB п к подпрограмме, начинающейся со строки п. Это возвращение задается оператором RETURN & конце подпрограммы. Пример. Построение программы с подпрограммой. Пусть нужно вычислить Описание программы приведено на с. 45. 10 INPUTЗАДЙЙТЕ ПОГРЕШНОСТЬ РЕЗУЛЬТАТА Е=Е ге INPUTВВЕДИТЕ !«;=Х: LETI=i: LETS=0 30 LETZ=S!LETS=S+X4I:LETI=I+2 40 IF S-Z>E THEN 30 50 PRINTAHT<X>=S 60 GOTO 20:END Оснодпая ОВраш,ени.вкПП1 ПП1 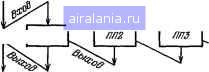 Программа Подпрограммы (ПП) Рис. 2.8. Структура организации подпрограмм с вложениями их друг в друга определенный интеграл /=5 -I2x+l dx=\ f(x)dx по простой формуле Симпсона /(a) + 4/()+/(fc) (2.1) В этом случае нужно трижды вычислить значение подынтегральной функции {х]= = -\l2x->t\ для х=а, {а + Ь)/2 и Ь. Поэтому вычисление f{x) целесообразно вынести в подпрограмму. и засекают время ее исполнения. Деля его на N, получают время исполнения пустого цикла *ц. Затем внутрь цикла вставляется команда с заданной операцией, например LET С = А + В, если нужно найти время проведения операции сложения. Снова определяют общее время вычислений и делят его на N. От полученного времени отнимают ta и получают время исполнения заданной операции to„. Время ion сильно зависит от,типа ПЭВМ, поэтому подобные испытания следует провести для конкретной ПЭВМ, имеющейся в распоряжении пользователя (разумеется, если нужных данных нет в ее описании). Ниже приведены типовые значения ton для СПП 10 INPUTВВЕДИТЕ ПРЕДЕЛЫ ИНТЕГРИРОВАНИЯ А,В А,В 20 LET!><=A: GOSUB 60s LETS=F 30 LET.!><=<A+B)/-2! GOSUB 66: LETS=S+4»iF 40 LETX=B: GOSUB 60: LETS=S+F 50 PRINTЗНАЧЕНИЕ ИНТЕГРАЛА I=S»i*:B-A)/6: STOP 55 retlПОДПРОГРАММА ВЫЧИСЛЕНИЯ FiX> 60 LETF=SQR iгжх+1>:RETURN 70 end Здесь подцрограмма с оператором возврата занимает строку 60. Суммирование членов в квадратных скобках (2.1) производится с помощью вспомогательной переменной S. Для а = 0 и 6 = 1 вычисления по этой программе дают результат /=1,398150843. Оценка времени вычислений производится суммированием времен выполнения отдельных операций с учетом повторяемости их в циклах и подпрограммах. Для приближенной оценки времени выполнения отдельных операций можно использовать следующую методику. Вначале определяют время проведения Л циклов (Л=100 или 1 ООО). Для этого, задав Л, пускают простейшую программу 10 FOR 1=1 ТО N: NEXT 1 20 PRINT END: END на базе настольной ЭВМ Электроника-ДЗ-28 и ПЭВМ класса Pocket Compnters FX-702P (<on в секундах):
0 1 2 3 4 5 6 7 8 9 10 11 12 [13] 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 0.0121 | |||||||||||||||||||||||||||||||||