Рис. 3.1. Декартова и сферическая координат

§ 3.7. Преобразования координат и векторный анализ

Преобразование координат из декартовых в полярные на плоскости описывалось в § 2.3. Преобразование декартовых координат X, Y, Z в сферические в пространстве (рис. 3.1) проводится по формулам

R=J¥+W+. Q = arctg()/X), q)=arccos(Z/y?),

где R - полярный радиус, Q - долгота и (р - широта. Обратные преобразования проводятся по формулам

X = Rs\n(fcosQ, Y = R ып (f cos Q, Z~ = R cos ф.

Таким образом, если положить Z = 0, ф = 90°, то из этих формул вытекают формулы для преобразования декартовых координат в полярные и наоборот на плоскости.

Программа 3.62. >

10 PRIHTnPEOEPftSOBAHME КООРДИНАТ В ПРОСТРАНСТВЕ

20 PRIMTC«rePM4ECK№< В ДЕКАРТОВЫ -КОД 0

38 PRINTДЕКАРТОВЫХ В СФЕРИЧЕСКИЕ-КОД 1

40 ХМРиТЗАДййТЕ КОД ASIF ft=l THEN 110 . !

50 ХНРиТВВЕДИТЕ ПОЛЯРНЫЙ РАДИУС R=R

60 1МРиТВВЕДИТЕ ДОПГОТУ-УГОЖГРАД) 6=QtLETQl=RftD<Q)

70 ХНРиТВВЕДИТЕ ШИРОТУ-ГОЖГРАД) F=F!LEtFl=RAD<F>

80 LETX=RieSIH<Fl>«C0S<Ql>tLETV=R9iSIH<Fl)9iSIN<Ql)

98 LETZ=R«COS<Fl>sPRIHTflEKftPTOBM КООРДИНАТЫ

100 PRIMTX=Xj-V=V»Z=Z5ST0P

110 ХНРиТВВЕДИТЕ КООРДИНАТЫ X,V»Z X»V,Z

120 LETR=SaR<X*X+V*V+Z9i2>!LETFsACS<Z.R)!LETe=ATNCV.X>

130 PRIHTПОЛЯРНЫЙ РАДИУС R=R, "ДОЛГОТА <a=IiE6«a)ГРАД

14в PRINTШИРОТА Р=ВЕ6<Р)ГРАД!ЕНВ

Пример. Для Л = 10, (3 = 40° и ф = = = 60° получим (код 0) ЛГ=6,634139482, )= = 5,566703992 и 2 = 5, а для X=)=Z=10 получим (код 1) Л =17,32050808, Q = 45° и ф = =54,73561032°.

Преобразование декартовых координат на плоскости при сдвиге и повороте координатных осей (рис. 3.2) осуществляется по формулам (далее е=(Э)

X=(X - Х„) cos С?+() - Id) si п Q, r={Y- )„) cos(3-(X-X.,) sin Q,

где X и Y - новые координаты точки (X, V), Ло и Id - координаты центра новой системы координат. Программа 3.83.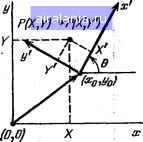

РиС; 3.2. Преобразование декартовых координат на плоскости при сдвиге и повороте осей

10 РКХЫТПРеОВРйЗОВАНИЕ КООРДИНАТ НА плос*;ости

20 ШРиТЗАДЙйТЕ УГОЛ ПОВОРОТА ПЛОСКОСТЕЙ СГРАД) G=G

30 LETO=RftIi«»! INPUTЗАДАЙТЕ КООРДИНАТЫ ЦЕНТРА XSVO В..С

40 ШРиТВВЕДИТЕ СТАРЫЕ КООРДИНАТЫ XV XV

45 LETXl=<X-B)i«COSCG>+<V-C)ii!SIN<Q): :

50 LETVl=<V-C)ii!COSC<a>-CX-B)ii!SIN<G> . :

60 PRINTНОВЫЕ КООРДИНАТЫ

70 PRIHTXl=XlrV1=V1!&0T0 40!EHII

Пример. Для Q = 20°, Xn = 3, У( = 2, = 5и У=5 получим

X =2,905445672 и )" =2,135037676.

Вектор (отрезок) с координатами начала (Xi, У) и конца (Хг, Уг), лежащий на

плоскости, имеет длину .

?=д/(X2-•xo+(У2-y•,)

Координаты точки (X, У), делящей этог отрезок в отношении M/N:-

J NX,+MX2 Ny\+MY2 Х=-..... . у=-

./И + Л/

/И + Л/

Ш PRINTДЛИНА ОТРЕЗКА И ЕГО ДЕЛЕНИЕ В ОТНОШЕНИИ МН

гв INPUTЗАДАЙТЕ КООРДИНАТЫ ТОЧКИ 1 KItVI

38 INPUTЗАДАЙТЕ КООРДИНАТЫ ТОЧКИ 2 ;.!2»V2

40 LETIi=SGR( (Х2-К1 >-2+(V2-Vl>2J

50 PR I NTДЛИНА ОТРЕЗКА Ii=Ii

60 INPUTЗАДАЙТЕ MjH M,H

70 LETX= < N*;>! 1+МЖК2 V t M+N >

80 LETV=<N«V 1 +M*V2>/a-1+N>

90 PRINTКООРДИНАТЫ ТОЧКИ ДЕЛЕНИЯ ОТРЕЗКА

100 PRINTK=K,V=V:END

;>UtV1

;>!2,V2

Пример. Для X, = 2.3, 1=4, 2 = 8.5 и 2 = 0,7 получим D = 7.023531875. Задав М = 3 и Л/= 2, пмучим А= 6,02 и )=2,02.

Полярными параметрами прямой АХ + + BY-\-C = 0, лежащей на плоскости (рис. 3.3), являются полярное расстояние от нее до точки (0,0)

я=1С/л/лЧв

и полярный угол Q, вычисляемый из соотношений

cos Q=+A/Ja + B\ sin Q=+B/Ia + B\

где знак - берется, если С> О, а знак +, если С<0.

Программа 3.65.

Прямая Ах+Ву+СО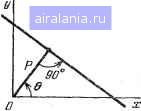

Рис. 3.3. Полярные параметры прямой на плоскости

10 PRINTПОЛЯРНЫЕ ПАРАМЕТРЫ ПРЯМОЙ АжХ+ВжУ+С=0

20 INPUTВВЕДИТЕ А,В,С (\,В,С

30 LETD=1!IF С>0 THEN LETII=-1

40 LETF=SQRС АжА+ВжВ>:LETP=ABS<С>/F

50 PRINTКРАТЧАЙШЕЕ РАССТОЯНИЕ ДО ТОЧКИ <0/0) Р=Р

60 PRINTС08С(а)=СжА/Р, SlH<Q)=Ii*B/F

70 PRINTyrofl Q=IiEGCACS<D»ft-F>):EHD

Пример. Для Л=3. В=-4 и С=10 получим Р = 2, cos(3=-0,6, sin (3 = 0.8 и (3=126,8698976°.

Вектор в пространстве с началом в точке (0,0,0) декартовой системы координат и концом в точке (X, Y, Z) имеет длину

и образует с осями координат углы a = arccos (X/D), p = arccos (Y/D)

у = arccos (2/D). Программа 3.66.

10 PRINTДЛИНА ВЕКТОРА И УГОЛ МЕ№ДУ НИМ И КООРДИНАТНЫМИ ОСЯМИ

20 INPUTЗАДАЙТЕ КООРДИНАТЫ КОНЦА ВЕКТОРА K/VZ X,V>Z

30 LETD=S(aR < КжХ+V*V+Zii!Z > s LETA=X/ti: LETB=VD: LETC=Z>Ii

40 PRINTCOS АЛЬФА=А,COS EETA=B/COS ГАММА=С

50 PRINTftj1b4>A=DE&i:ftC:StA>)>EETft=i)EG<ACS<:B>>,

60 PRINTrAMMA=DEG<ACS<C>>".&OTO 2esEND

Пример. Для Х = 2. Y=~2 и Z= -1 получаем cos а = 0,666666667, cos р = = -0,666666667, cosv=-0,333333333, а = = 48,189685Г, р= 131,8103149° и v = = 109.4712206°.

Два вектора с началом в точке (0,0,0) и концами в точках {Х\, Vi, Zi) и (Хг, Y2, Z2) образуют между собой угол (рис. 3.4)

X,X2+Y,Y2 + Z,Z2 Q = arccos - -•

Vxf+yf+z! -sIxl+Yl+zl

Длина отрезка, заданного концами этих векторов или просто точками с их-координатами,

D={X,-X2f+(Y,-Y2f + {Z,.

Координаты точки (X, Y, Z), делящей этот отрезок в отношении M/N, выражаются формулами

NX, + MX2 M + N

NZ,+MZ-, " M + N

NYi+MY2 M + N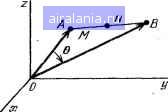

Рис. 3.4. Отрезок в пространстве, образованный двумя векторами, исходящими из точки (О, О, 0)

Программа 3.67.

10 PRINTVrOn МЕШДУ ДВУМЯ ВЕКТОРАМИ, ДЛИНА ОТРЕЗКА МЕ!ИДУ--

£@ PRINTHK КОНЦАМИ И КООРДИНАТЫ ТОЧКИ,ДЕЛЯЩЕЙ ОТРЕЗОК В

30 PRINT ОТНОШЕНИИ WW

40 РРШТВВЕДИТЕ КООРДИНАТЫ КОНЦА ПЕРВОГО ВЕКТОРА

50 INPUT;>!bVb21 А,В,С

60 PRINTВВЕДИТЕ КООРДИНАТЫ КОНЦА ВТОРОГО ВЕКТОРА

70 IHPUT;>S,V£,Z£ Ii,E,F

80 LETS=SQRСtA-IO"£+(В-Е)£+<C-F)>

90 LETG=SQR(АжА+ВВ+СжС)*SQR(СжП+ЕжЕ+РжР)

100 ЬЕТа=<Аж11+ВжЕ+СжЕ)Й

110 РР1НТ!.Г0Л МЕ!ИДУ ВЕКТОРАНИ<ГРАД) G=DE&CftCS(G.O)

120 РРШТДЛИНА ОТРЕЗКА Ii=S

130 1НРиТЗАДАйТЕ М,Н M,H!LETR=M+H

140 LETL=A!LETK=D!GOSUB 190!LETX=W

150 LETL=B;LETK=E!GOSUB 190:LETV=ll

160 LETL=C:LETK=F:GOSUB 190!LETZ=W

170 PRINTКООРДИНАТЫ ТОЧКИ ДЕЛЕНИЯ

180 PRIHT;>!=;>!,V=V,2=2!G0T0 13©

190 LETW=(H*L+M*KVR:RETURN:ENE

Пример. Для векторов A\ (8; -3; 8) и A2 (6; -1; 9) получим (3=14,6712486° и D = 3. Задав М=1 и Л/= 4, находим Х = 7,6, К=-2,6 и 2 = 8,2.

Плоскость в пространстве декартовой системы координат, описываемая уравнением AX + BY + CZ+D = U, имеет полярные параметры (см. рис. 3.5)

p=!Di/Ve+c-.

a = arccos (ТЛ/д/Л+Д + С), B=arccos (

у = а rccos (+ C/V ЛЧ+С),

где Я - кратчайшее расстояние от точки (0,0,0) до плоскости, а, р и V - полярные углы (между перпендикуляром, опущенным на плоскость из точки (0,0,0) и осями координат).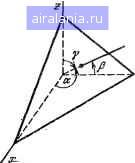

ЛерпЕндикуляр /(птекости

Плотовть

Рис. 3.5. Полярные параметры плоскости, расположенной в пространстве