

|
|
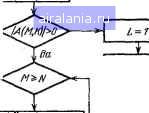
Главная -> Справочник по алгоритмам 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 [24] 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 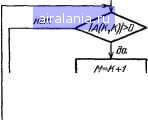
 BM=V;)=B[H)M A(K,L)A(M,L)  B(lhB(I)-A(I,K)* -v~z 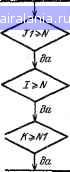 1=1+1 „у;- В(М) М=М-1 ± S=S+C(MM +7)*Х(1Л7}  L4l + X(MH[N)~S\  Рис. 4.1. Алгоритм реализации метода Гаусса с выбором главного элемента .10 РРШТРЕШЕНИЕ СИСТЕМЫ ЛИНЕйНЫК УРАВНЕНИЙ :15 PRINT МЕТОДОМ ВРАЩЕНИЯ 20 INPUTВВЕДИТЕ ЧИСЛО УРАВНЕНИЙ N=N!LETM=0:DIM ACHN) 25 FOR 1=1 ТО И: FOR J=l ТО N 30 PRINT!2.0!ВВЕДИТЕ. КОЭФФИЦИЕНТ А 1, .J 40 INPUT Aa»J)!IF .JON THEN 60 50 PRINTВВЕДИТЕ ВI:INPUT A<I>0J 60 NEXT J:NEXT I F0 FOR 1=1 TO H-i:FOR.K=I+l TO N S0 IF А<ЬП<>6 THEN U0 90 IF ft<K,IK>0 THEN lie 100 LETM=15LETL=0!&OTO 130 :i 10 LETM=SGR<fta, I>"2+A<K, I>"2> 120 LEtL=-A<KyI>/M!LETM=A<bIVM 130 FOR J=l TO H!LEtR=;Miiffta,.J)-LJ«ftCKr.J> 140 LETA<K>J>=LsKft<bJ)+M!«A<K,.J) 150 LETA(I,J>=R!HEXT J 160 кЕТР=МжА<Ь0>-кжАСК,0) 170 ЬЕТА<К/0>=кжА<1,0)+МжА<К>6) 180 LETA<b0)=R!NEXT KI: NEXT I iSe FOR I=H TO 1 STEP -1!LETM=0 200 FOR K=0 TO N-I-1 , 210 ЕЕТМ=М+А(е,Н-К)жА<:ЬН-К)!НЕХТ К £20: LETAC0/ I >=*:А< Ъ 0>-*1)/A< Ы > 230 PRINT!2.e!КОРЕНЬ XI =ГР1.9!A<6, I> 240 ЬСХТ I:END Для проверки программы можно решить уравнение (4.3). Результат совпадает с указанным выше I Метод простых итераций, описанный в § 4.4 для систем нелинейных уравнений, применим и для решения систем линейных уравнений. Однако его сходимость гарантируется, если значения диагональных элементов матрицы А(1, J) превосходят остальные, что снижает применимость метода простых итерации (хотя любые системы линейных уравнений можно свести к нужному для сходимости виду с помощью преобразований, описанных в [7]). Сказанное относится и к методу Зейделя. Программы реализации этих и некоторых других методов частного примейения Даны в Приложении 5. Отметим, что итерационные методы Обладают свойством самоисправления ошибок в ходе вычислений и могут применяться в особых случаях, например, когда матрица коэффициентов щ сильно разрежена, .т. е. «одержит много йулей. Метод минимизации заключается в поиске минимума целевой функции F{X,, .Х2, Xr)\f\{Xx, Х2, .... Хп)[ + .-- ... + f2(X, Х2, ...j Х„), компоненты которой формируются из урав-неиййг решаемой системы fi{xi, Х2.....Xo)=a,iJi:i+012X2+... I ...-\-ainXri-b\, U{Xu Х2, Xh) = a2iXi+022j;2+..: ; ...+а2„Х„~б2. ]Лхи XI, л:;)=о„1Х + о„2Д;2 + .-- i ...+0„„Х„-fc„. Есзи х\, Х2, х„ - решение (4.1), то функ- ция F(xi, Х2, х„)=0. Для реализации этого метода могут использоваться программы поиска минимума функции ряда переменных, описанные в § 5.6. § 4.2. Интерполяция и экстраполяция Интерполяция функции у (х) одной переменной X. заданной (« + 1) узлами yi(x,), где г==0, \, 2, ..., п, заключается в нахождении значений у по значениям х, находящихся в промежутках между узлами Xi. При интерполяции функция у (х) заменяется инт терполяционным полиномом Р (х), значения которого Р (xi) в узлах точно совпадают с у (xi). Значение п задает степень полинома Р (х). Формулы Лагранжа для интерполяции при равномерном расположении узлов обеспечивают наименьшее время интерполяции, не требуют обновления ввода yi и хо для вычис ления каждого у(х) и позволяют вычислять yi в узлах Xi (например, для контроля правильности вычислений). В этих формулах индексом О обозначается центральный узел. Для п + 1=2ч-6 формулы Лагранжа имеют вид [36] - у(х)2=( 1 р)(уо + р!/1 + 0,125Ау"(9; ,(.x)3=4lli), ,+(l-p),„+£(P±.n„+- + 0,065A(/"(g); (р-1Хр-2) -Уо - р(р+\)(р-2) ,р{р-1) y2+R(p), !;<p< -1 + (;j=-lHp-4). {p?-!)p(P.+ 2> где. fO,»12ftV© при Ip.Kl, tft031AV<g) при r<fp<2: ..P(p-l)(p-2)(p-3) 120. p(fl-lMp-4)(p-3) ,
.0,0049AV(b) при 0.<р<1, при 1<р<;о,. 1<р<2, •0Д24 при.~2<р< -i, 2<р<3. В этих формулах х=хс + рг, p=(xxo)/h, где Л - шаг расположения . узлов, индекс у 4((х) соответствует числу узлов (/г+1), у" (Ю - максимальное значение производной з/,х) для точки x = g, лежащей в пределах интерполяции. Последний член формулы (он в программах не вычисляется) характеризует погрешность интерполяции. Пример (к программе 4.4). Для контроля этой программы выполним интерполяцию функции Струве Яо {х)=у{х) [36], заданной таблицей, при- дг„=1 и /:=0 2: у.-2 = 0,36699114; =0.4739944; № = = 0,5686566; у, =0,648855; {/2 = 0.7117925 и №0,7570255. !. При линейной иитерполяции (M = l) для х=1.! получ-нм (1,1) =0,6087558. 2. При квадратичной интерполяции (Af = 2) получим (/.(0,9) =0,5531716; {/(1,1) = = 0,6104494. 3. При кубической ннтерполнцни (М=3). получим (/(0,9) =05230539688; y(i.l) = = 0,6105670ЙЗ. 4. При /И = 4 получим y{S),g) = = 0,5230357695; !/(l,.i;) =0,6105779508. 5. При . М=5, получим (/(0Д).= = 0,5230350945; {#{1Л )= 0,6105786258. .. PRINT№!ТЕРПОЯЯЦИЯ ПРИ H=COHST РО ФОРМУЯАМ ЯАГРАНША ГНРОТЗЙДАЙТЕ СТЕПЕНЬ ПОШНОМА М=1-5 H=M!LETH=M+1 33 1НРиТВ8ЕйИТЕ Х0»К ZHslF N=3 ТНЕН 100 • :- 43 IF 14»=4 THEN 143 50 IF Н»5 ТНЕН 193 т IF Н=6 ТНЕН 250 78 INPUTВВЕДИТЕ VeVl А*В 80 INPUTВБЕЙИТЕ X=XU,£TP=<X-Z>/H 90 tETV»<l-P>»A-P»BsPRIHTV»V!60T0 80 ie@ нр«тВВЕДИТЕ y-i,ve,vi ft,в,с lie INPUTSBESHTE X=XSLETP=<X-Z>-H 120 LETV=P»<P-l>»ft2+<i-P«P>ssB+P«<P+l>«C>2 13Э psiHTv=V!eoTO 110 140 INPUTВВЕДИТЕ VIV2 A»B,C»B 150 INPUTВВЕДИТЕ X=XstETP=«--Z>-HtLETE=<P-2)2 160 LETy=-P!«<P-l>aEsft>3+<P«P-l)»ES!B 170 LETV=~P«<P+l>«E»C+P«<P!6P-i>itEll/-6 180 PRIHTV==Vs60T0 150 190 IHPUTBBEftHTE ¥-2,¥~1»У0»У1»Уг ApB»C,B»E 208 1Н?ПЛВВЕДИТЕ X=X8LbTF=<X-Z>/-H 21s LETF>=<f«P-l).28LETK=<P*P~4>-2 220 LETV-F»P«<P-2>aA.i2-<P-l>жРжКжВ./3+р1«К«С 230 LETV=V-<IP+i)»Р8!КаВ>3+РжР»<Р*2)жЕ12 240 PRIMTVVsBOTO 200 230 IHiPUTВВЕДИТЕ У-грУ-1»У0»У1»Уг,УЗ Л,В»С>В»Е»Р S60 1НРиТВВЕаИТЕ X*Xi!LETP=<X-2>>HtLETM=P«P-! 270 LETI=«-24tLETJ=~P»I«<P-3>!tETK=M-3stETL=KS!CP-3>12 280 LETY=ai3!<P-2>S!ft/5*t)eiPS!<P-l>«B2-M»LS!C гэа LETV=«V*Pa<P+i)«taE+J»<P+2)*!E+FKlsiK«F/5 Ш PRSKTV=yt60T0 260SEHI) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 [24] 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 0.0115 | ||||||||||||||||||||||||