При аппроксимации неоднократно используются п. 2, 3 и 4 алгоритма. Общее время вычислений примерно в 4 разя больше, чем при квадратичной интерполяции - аппроксимация функций одной переменной.

Программа 4.10.

всех корней сводится к локализации каждого корни с последующим сужением отрезков локализации корня [с, Ь\ одним из описанных далее методов.

le РР1НТМН0Г0ИНТЕРРАЛЬНАЯ ДВУКМЕРНАЯ КВАДРАТИЧНАЯ

Se PRINTИНТЕРПОЛЯЦИЯ-АППРОКСИМАЦИЯ ФУНКЦИИ FiXrW>

30 INPUTЗАДАЙТЕ ЧИСЛО ТОЧЕК КАЖДОЙ КРИВОЙ M=M!LETM=M-1

40 INPUTЗАДАЙТЕ ЧИСЛО КРИВЫХ N=N!LETN=N-l!riIM РШгЮ

50 INPUT ЗАДАЙТЕ XOrVO А/В

ее INPUTЗАДАЙТЕ ПРИРАЩЕНИЯ ПО X И V - H,L H,L

70 FOR 1=0 ТО NSFOR J=e TO M

80 РР1НТ.3.0!ВВЕДИТЕ V.I,J: INPUT Fa»J>

90 NEXT Jг NEXT I

100 INPUTВВЕДИТЕ VX V/XS60SUB 4000 110 PRINT!F1.9!PCX,V>=Z!60T0 lOO 4000 REMПОДПРОГРАММА ВЫЧИСЛЕНИЯ F<X,V) 4010 LETJ=INT<<X~A>-H)!IF J=0 THEN LETJ=1 4020 LETI=INT<i:v-B)..L>:IF 1=8 THEN LETI=1 4030 LETP=<;X-A-J*H)>-H! LETQ=<V-E~I*L>L 4040 LETI=I-l!60SUB 4088!LETC=2 4050 tETI=I+2!60SUB 4080!LETE=2 4060 LETI=I-l:60.SUB 46803 LETri=Z

4070 LET2=Q*<Q-1 JskC-S-K 1-е*0)жГ1+0ж<0+1 )жЕ>-2!RETURN 4080 LET2=P* < P-1 > *F < Ь J-1 > -S* < 1 -P*P > *F a r J > 4090 LETZ=Z+P*<P-t-l>*F< I, J+1 )-2!RETURN:END

Пример. Пусть требуется провести интерполяцию для семейства вольт-амперных характеристик мощного полевого транзистора {Fix. у) = 1сШ<:. Уз), где /г - ток стока, л:=Сс - напряжение на стоке и y=U,- напряжение на затворе), если она задана таблицей = М=6, А = 10, /=1, f/„ = 3, xc = 0):

Метод простых итераций осно,ван иа представлении (4.4) в виде

xHix) (4.5)

и многократном применении итерационной формулы Xi,+i=i{x„) до тех пор, пока соблюдается условие

\х., + ,-х„\е, (4.6).

Значения токов приведены в амперах. Введя эти данные, будем получать F(35; 5,5)= 1,631875 А; F(45; 7,5Ь=3,8375 А и т. д. Отметим, что этот метод обеспечивает высокую точность аппроксимаций для семейств достаточно сложных крипых, в том числе не монотонных.

§4.3. Решение нелинейных и трансцендентных уравнений

Решение нелинейных (в частности, трансцендентных) уравнений вида

F(x) = 0 (4.4)

заключается в отыскании одного или всех корней на отрезке [а, Ь] изменения х. Обычно стараются локализовать каждый корень в своем отрезке [а, 6]. Тогда нахождение

где Е - заданная погрешность вычисления корня х. Итерационный процесс сходится (т. е. Хп-х при оо), если соблюдается условие f (х)<1 при a<jc<&. Программа 4.11.

в строке 70 программы 4.11 записано выражение f{x)=sin je + 0,25 (подпрограмма), соответствующее решению трансцендентного уравнения

F(je) = Je-sin л- -0,25=0. (4.7)

Для начального значения х=хо-1,2 и погрешности t=£=!.IO* получим х= = 1,71230493 при времени счета около 5 с.

Метод Ньютона (касательных) основан на замене F{x) в точке начального приближения х=Х() касательной, пересечение кото.-рой с осью X дает первое приближение Xi. и т. д. (см. рис. 4.4). Таким образом, итерационный процесс схождения к корню реали-

зуется формулой

x„+,=x„-F(x„)/F(x„),

(4.8)

до тех пор, пока соблюдается условие (4.6). Метод обеспечивает быструю (квадратичную) сходимость, если

F(x„) F"{xo)> 0.

(4.9)

В качестве хв выбира1.от тот конец отрезка [а, Ь], иа котором знаки F{xd) и f"(хо) совпадают. Выигрыш во BpewiCHH вычислений за счет быстрой сходимости уменьшается нз-за необходимости вычислбния помимо F{xn) производной F{x„). Исключение составляют частные случаи, когда, выражение, ito которому вычисляется FI х„)/F(x„), не сложнее выражения для вычис:ления F{x„) отдельно.

Программа 4.12.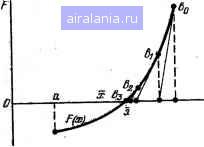

Рис. 4.4. Решение уравнения F (х) =0 методом Ньютона (касательных)

10 PRINTРЕШЕНИЕ УРАВНЕНИЯ Fi:X)=0 МЕТОДОМ HbKiTOHA

S0 :INPUTЗАДАЙТЕ НАЧАЛЬНОЕ ПРИБЛИМЕНИЕ Х0=Х

25 INPUTЗАДАЙТЕ ПОГРЕШНОСТЬ РЕЗУЛЬТАТА Е=Е

30 aO-SUE 6e!LETX=X-F

40 IF AB.S<;F)>E THEN ЗО

50 PRINTКОРЕНЬ УРАВНЕНИЯ Х=Х:60Т0 20

55 REMПОДПРОГРАММА ВЫЧИСЛЕНИЯ F<X>>-aiF>-DX)

60 LETF=<X-SIHi:X>-.25)/-a-C0S<X)>

70 RETURN!END

Пример. Вычислить корень, уравнения (4.7) на отрезке [1,1; 1,2]. В данном случае F(x)= 1 -cos x, так что

fl(x„) x-sin л; -0,25 F{xn) ~ I-COSX

Вычисление этого выражения оформлено подпрограммой, з.чписанной со строки 60. Поскольку F" (x)==sinx>0 и F(x)>0 при х = Ь, в качестве начального приближения возьмем хо = 6=1.2. Тогда при погрешности е=Ы0- получим л:= 1,171229656 при времени счета <c»3,f> с.

Модифицированный метод Ньютона заключается в том, что вместо вычисления производной Р (х„) на каждом шаге итераций находится ее приближенное значение F(x„) =dF{x„)/dx (F(x„ + &x) -- F(x„) )/Ax = AF(x„)/Ax, где Ax=e. Следовательно, итерационная формула имеет вид Ах F[x„)

=х„-

F(x„+Ax)-F(x„).-

Значение Ах не обязательно должно быть равно 8. Равенство Ах=е позволяет уменьшить число- исходных данных при вводе.

Программа 4.13.

10 рр1итРе:шение уравнения f<x)=0 модифицированным

15 PRINT методом НЬЙТОНА

2>0 INPUT3-.дайте начальное ПРИБЛИЖННЕ Х0=Х

25 inputзадайте погрешность результата .Е=е

30 &05ш 70S LETL=F! LETX=x+E

40 &OSUe 70:LETL=E*L-<F-L)!LETX=X~L-E

50 IF ABS<:L)>E then 30

60 PRINTкорень уравнения Х=Х:60т0 20

70 LETF=x--SIN<x)-.25

80 RETURN:END

10 рр;):нтре:шение уравнения x=f«) методом

15 priht простых итераций

ги INPUTзадайте начальное значение X Х0=Х

s5 INFUTзадайте погрешность результата" е=е

30 &оьив 7е

40 if ABSCF-XXE THEN 60

50 LETX=F:60T0 30

60 PR INTкорень X=X! 60T0 so

65 REMподпрограмма вычисления F<X>

70 LfcTF=SINi:X>+.s5

75 REiTURNsEHD

Пример. Вычисление f(x„) выполняется подпрограммой, записанной со строки 70. Для приведенного выше примера расчет дает х= 1,171229653 при <с~\ с. При модифицированном методе Ньютона>тпадает необходимость вычисления F{x„), но добавляется вычисление F{x„-\-Ax).

Метод Рыбакова также можно рассматривать как модификацию метода . Ньютона при замене F(Xn) некоторым числом М где I - значение х иа отрезке [а, Ь\, при котором F{x) максимальна. При AJ:§>f() сходимость не нарушается, но замедляется. Метод Рыбакова удобен для поиска всех корней уравнения (4.4) на отрезке [а, Ь\ с помощью следующего алгоритма [24].

1. Задаем начальные значения х=хо=«.

2. Для каждой и-й итерации (п = 0, 1, 2, ...) вычисляем

х„+,=х„+-Ь (4.10)

Метод делёния отрезка [а, bj пополам (метод дихотомии) реализуется следующим алгоритмом (для F (с) > 0).

1. Находим х==(а + Ь)/2.

2. Вычиьпяем .(х).

3. Если F(x)> О, задаем о=х, иначе Ь - х.

4. Проверяем j/словие Ь -а> е; если оно выполняется, идем к п. 1, если не выполняется, заканчиваем вычисления и считаем, что х=х с за.данной точностью е.

Число итераций при использовании этого метода

In ((fc -a)/el

Л/~-

In 2

и проверяем условие

х„+,<6. (4.11)

Если (4.11) не выполняется, значит, найдены все корни. В противном случае проверяем выполнение условия x„+i-х„> е. Если оно выполняется, повторяем цикл вычислений по формуле (4.10). Если это условие не выполнено, значит, х„+1 есть один из корней и значение x„+i выводится на печать. После этого переходим к выполнению следующего пункта.

3. Задаем начальное приближение к очередному корню хо = х„+1-(-е и, если хо<6, идем к выполнению п. 2. Если хоЬ, вычисления считаем законченными.

Число итераций при реализации метода Рыбакова N={b-a) М/е. Функция F (х) на отрезке [а, Ь\ может иметь производную с разрывами первого рода.

Программа 4.14.

значительно, к поэтому сходимость его медленная. Однако при любой ширине отрезка [а.. Ь] сходимость гарантирована. Кроме тогО, простота реализации метода уменьшает число вспомогате.1Ьй ых операций и частично компенсирует увеличение обш.его времени счета из-за медленней сходимости. Программа 4.15.

Пример. Для уравнения F(x)=E-x- W.4(exp (Dx)-l) при Е=2, R = \0, h = Ы0~. D = 20, Л=0, В = 2 и е=Я = = \.\Q-\ Получим х=0,8143920898. При F (а)<0 берем F (x):=-F (х).

Метод поразрядного приближения для поиска всех корней сп-резка [а, Ь] реализуется следующим алгоритмом.

1. Задаем шаг c=h.. х=а, k-Q и находим U7=sgn F(x).

2. За.даем значение .х={х-\-с) и проверяем условие (х-с)>6. Если оно выполняется, заканчиваем счет, инач«! идем к п. 3.

3. Вычисл;?ем F{x) и проверяем условие FW/0 0. Если оно выполняется, идем к п. 2, иначе к п. 4.

4. Задаем c=-c/R, где R - показатель разрядности (уменьшени!? шага с), и проверяем выполнение условий! \c\>b/R, где е -

16 PRINTнахождение всех корней уравнения F<X)=Sii 15 PRINTB интербале от а до в методси рыбакова

ге INPUTвведите границы интервала А,Б а,в

£5 INPUTзадайте погрешность-нахождения корня е=е

Зе 1НРиТЗАДАйТЕ число M=MiLETX=A!LETT=e!LETI=0

40 OOSUB. 1£0!LET2=X+ABS<F)1

50 IF 2>=в GOTO 115

60 IF Z-X>=E OOTO 90

70 IF T=0 THEN LETW=Z

80 LETX=Z+E!LETV=Z!LETT=ls&OTO 48

90 IF TOl THEH 110

100 LETI=I+l!PRIHT!.2.0!Xr= !F1.9! <V+iW>SsLETT=«

110 L£TX=2:CiOTO 40

115 PRINTконец вычислений!STOP

120 LETF=X4-13*X2+36

130 RETURN!END

Пример. Найти все корни, уравнения /=(х)=х*-13x-f 36 = 0 иа отрезке [ - 4,41, т. е. а=-4, 6=4, с точностью е=Ы0~ Задав М=100, получим: х, =-2,9987453; Х2=-1,999170328; Хз = 2,000132432 и Xi = =3,000785311. Общее время вычислений около 2 мин.

заданная погрешность вычисления корня. ; Если это условие выполняется, идем к п. 2, , иначе к п. 5.

5. Задаем k=k-\-l и вы.водим на печать (индикацию) значение k-ro корня х*=х. Затем полагаем c=h, W~ - W и идем к п. 2.