ei PRIHTPEIUEHHE УРАВНЕНИЕ F<K>=e МЕТОДОЙ ДИХОТОМИИ

05 INPUT Е, RrlOrB E,R,I0fD

10 INPUT A, B..H Af BrH

SO LETX=<A+EOS

30 60SUB Э0

40 IF F>0 THIEN 60

50 LETB=X: ЬГЯО 7©

60 LETA=X

70 IF B-A>H THEN SO

80 PRINT KOPEHb=X! STOP

90 LETF=E-X-R «10* < EXF4 D*X >-1>

100 RETURN". BSD

Программа 4.16.

10 PRINTВЫЧИС1ТЕНИ1Е ВСЕХ KOPHEvi НЕЛИНЕЙНОГО УРАВНЕНИЯ F<X>=0

20 PRIHTВ ИНТЕРВА.ПЕ <АгВ> МЕТОДОМ ПОРАЗРЯДНОГО ПРИБЛИЖАЯ

30 INPUTЗАДАЙТЕ ГРАНИЦЫ ИНТЕРВАЛА А,В А,В

40 INPUT»»ДАЙТЕ тГРЕШНОСПЬ ВЫЧИСЛЕНИЯ КОРНЕЙ Е=Е

50 INPUTЗАДАЙТЕ illftr НАЧАЛЬНОГО ПОИСКА Н=Н

60 LETC=H!LETK=0!LETX=A:GOSUB 120tLETW=SBN<F)

70 LETX=X+C:IF Х-С>=В THEN РР1НТК0НЕЦ-.STOP

80 GOSUB 120s IF F*UiC>0 THEN 70

90 LETC=-C-4s IF ABS<C>>E-4 THEN 70

100 LETK=K+lsPRINTUV.0!XK!F1.9!=X

118 LETC=HsLETW=-W!f.OTO i&

120 LETI=.2718*X*EXF4:-18*X)+1E-8«CEXP<20«X)-1) 130 LETF=<1~X)-125-I sRETURNsEME

Пример. Найти напряжения hei туннельном диоде из решения уравнения

FiU)=(E-U)/P-l{U)=0, (4.!2)

где Е - напряжение источника питания, R - сопротивление в его цепи и

- Л/образная вольт-амперная характеристика туннельного диода. Для x=U, А =0,2718, (х=10, £>=1-10 . Р = 20, f=i В и /?=125 0м получаем подпрограмму, Записанную в строках 120 и 130. Задав а = 0, Ь = Е и е = £1 =0,001, получим Xi = 0,043 В, Х2 = 0,234 В и хз = 0,625 В. Следовательно, в данном случае линия нагрузки резистора R пересекает вольт-амперную характеристику в трех точках.

Метод подекадного приближения аналогичен методу поразрядного приближения при R=\0. Метод дает все верные цифры результата в пределах заданной погрешнэсги е (остальные цифры - нули).

Метод хорд (см. рис. 4.5, а). При этом методе каждое значение x„+i находится как точка пересечения оси абсцисс с >;ор,10Й, проведенной через точки F(a) и F{b), причем одна из этих точек фиксируется - та, для которой знаки Щх) и F"{x) одинаковы. Если неподвижен конец хорды х = а, то

Х„+1=Х„-

F{x„)-F(a)

(х„-а).

а если неподвижен конец хорды x = fe, то

F(b)-F(x„)

\b-x„).

Если

U-„+i-х„> е,

то в первом случае считаем Ь=Хп+\, во BTCipoM а = х„+\ и повторяем вычисления. При использовании метода хорд полагается, что корень X находится на отрезке [а, Ь].

Метод секущих (см. рис. 4.5, б) реализуется алгоритмом, описанным выше, если абсциссы а t\ b взяты с одной стороны от корня и не фиксируются.

Необходимость вычисления F (х) (условия скодимости этих методов аналогичны . (4.9)) и выбора одной из двух формул затрудняют практическое применение методов хорд и секуш.нх в отдельности.

Комбинированный метод секущих - хорд обеспечивает гарантированную сходимость при выборе в пределах отрезка [а, Ь] двух приближений: нулевого хо и первого xi. Он реализуется алгоритмом, описанным для метода Ньютона с заменой производной F{x) ее приближенные значением - множитель перед F {х„}:

Х„ -Х„ 1

F {x„)-F (х„ ,)

Программа 4Л7.

т PRINTРЕШЕНИЕ УРАВНЕНИЯ РОО=0 КСЦБИНИРОВАННЫМ 0S PRINT МЕТОДОМ СЕКУЩИХ-КОРД

05 INPUT ERjI0-rDEfR.. 10;Г.

10 INPUT УВгУЛгИ т> хь и

£0 LETX=Xe: &OSUB ВО

30 LETA=F! LETK=Xl! &OSUB 80

40 LETB=F! LETV=X0-Ai«<Xl-Xe.O>-4E-A)

50 LETX0=X1! LETX1=V

60 IF ABS<X1-X0)>H THEN 20

70 PRINT KOPEHb=Xl! STOP

m LETF=E-X-R*I0*:EXPai*X>-i>

90 RETLlRNs ENE

100 RETURNS END

Рис. 4.5. Решение уравнения F {x) = = 0 методом хорд (a) и секущих (б)

Пример. Для уравнения F{x)=x+x - - x-l при хо=2, xi = l,5 и 8==Ь!0 находим 7=1 при ic»10 с. Аналогичный результат получим при xo = 0,5 и л- = 1,5. Вычисление F(x) оформляется подпрограммой, записанной со строки 90.

Метод Эйткена - Стеффенсона с ускоренной сходимостью обеспечивает решение уравнения (4.5) по следуюш.ему алгоритму.

1. Задаем начальное приближение л:„.=хо.

2. Находим первое X\-f(xa) и второе jC2 = f(xi) приближения.

3. Вычисляем х„-(.1= (хоХг -x:i)/(xo -2x,f

+ Х2).

4. Проверяем условия x„+i-х„>е, хо-2х+Х2=50. Если эти условия собл.ю-даются, идем к п. 1, т. е. задаем х„ но:вое значение x„+i, в противном случае останавливаем счет и получаем x=x„+i.

Метод Эйткена - Стеффенсона при сложных f(x) имеет ускоренную сходимость (по сравнению с методом простых итераций}. Однако при простых функциях /(х) время счета практически не уменьшается, тан; как число дополнительных операций в этом методе существенно больше, чем в методе простых итераций.

Программа 4.18.

П р и гй е р. Используя данные к программе 4.П, п,ри е=!-10~ получим корень (4.7) х=1,17Ц!29421 при <с«;7 с. Вычислениефуик-ции f(x) выполняется подпрограммой, записанной в строках 90 и 100.

Метос) обратной интерполяции - экстраполяции заключается б вычислении ряда значений t/, = f(x,) для заданных х,- на отрезке [а, Ь]. .Затем, полагая у = 0, с помощью обратной интд)поляиии находим х, (рис. 4.6, а). Корень южeт быть найден и за пределами отрезка [а, Ь\ (рис. 4.6, б). В последнем случае п)>именяется обратная экстраполяция. Для реа.аизации этого метода могут использоваться описанные в § 4.2 программы.

К сожалению, для произвольных F{x) оценка погрешности этого метода отсутствует. Однако для получения результата с заданной погрешностью можно построить итерационную! процедуру уточнения корня. Отметим, что при т=2 отсчетах F{x) данный метод фактически является комбинированным методом секущих - хорд," реализуюш.им линейную интерполяцию - экстраполяцию.

Метод обратной квадратичной интерполяции - экстраполяции заключается в замене F{k) полиномом .Лагранжа второй степени (число отсчетов т = 3). При этом можно

05 PRINTPEfflEHHF£ УРАВНЕНИЯ ,4=:F<:X) МЕТОДОМ

10 PRINT ЭйТКЕНА-СТЕФФЕНС;0НА

15 1НРиТЗАДнйТЕ «НАЛЬНОЕ ПРИБЛИКЕНИЕ Х0=Х

20 INPUTЗАДАЙТЕ ПОГРЕШНОСТЬ РЕЗУЛЬТАТА Е=Е

30 LETA=x5 60SUB.- 90:;LETB=F:LETX=F

40 .60SUB 90: LETC=<A-2SKB+F>

58 IF C=0 THEN 70

60 LETX=Ch*F~E*B>.-C

70 IF ABStX~F>>E THEN 30

30 PRINTКОРЕНЬ УРтеНЕНИЯ X=X:GOTO 26

Эе LETF=Sl>KX.+.25

100 RETURN! EWD

y=F(w)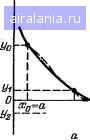

Парабола

x,x-.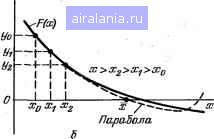

Рис. 4.6. Решение уравнений F(x\=V> методом обратной интерполяции (а) и экстраполяции (б)

получить аналитическое выражение для приближенного значения корни.

Дейетеительно, заменив л-- иа у и г/ на л-, полином Лагранжа второй степени можно представить s виде j:(!/) = foo + &i(i/ -t/o) +

Сходимость данного алгоритма основана на свойстве интерполяционного полинома давать точные значения х при заданном у-е узле интерполяции (т. е. в точке xi).

Программа 4.-19.

le PRINTРЕШЕНИЕ УРАВНЕНИЯ Г(Х>=е МЕТОДОМ КВАДРАТИЧНОЙ

ге PRINT ИНТЕРПОЛЯЦИИ-ЭКСТРАПОЛЯЦИИ

зе INPUTЗАДАЙТЕ ГРАНИЦЫ А,В

35 1ЫРиТЗАДАйТЕ ПОГРЕШНОСТЬ ВЫЧИСЛЕНИЙ Е=Е

40 ШРиТЗАДАйТЕ НАЧАЛЬНОЕ ПРИБПИШЕНИЕ Х1=С

50 LETX=A!60SUB 120!LETL=F

60 LETX=B!C<>SUB 120SLETM=F

70 LETX=C!60SUB 120!LETQ=C

80 LETN= <C-A)(F-L)!LETP= <B-A)<M-L)

Э0 LETC=A-LiK<N+<N-P>iKF/<!n-F)>

100 IF ABS<Q-C)>E THEN 70

118 PRINTKOPEHb X=C!ST0P

120 LETF=X-SIH<X>-.25!RETURN!END

+ 62(1/-t/o)(t/ -t/i). Для i/=0 находим

x - bb - b\ya + biyi\. (4.13)

В соответствии с методом Эйткена и с учетом взаимной замены переменных х у имеем

6о=Х1, Ь\

ху - хр

Х2 - Х1 , . 1?2 -6

1/2 -4/0 У-у\

Подставив foo, fci и 62 в (4.13), после элементарных преобразований получим

- /л--.1-,,

л = хк-Уй { - 4-

\У-У«

[Xi -Xo)/(j/i - j/o)-(x2 -xn)/(t/i -ту.)) \ У-1-у\ )

(4.14)

Приведем алгоритм вычислений этим методом (один из возможных).

1. Полагаем хи = а и вычисляем F{x»)=ya.

2. Полагаем Х2 = Ь и выч>1сляем Р(х->)=у2.

3. Задаем начальное приближение к корню x=:xi и вычисляем F(xi)=i/i.

4.По формуле (4.14) находим корень x (см. рис. 4.6).

5. Г!роверяем условие Ix - xiI> f; если оно выполняется, задаем х\-х и идем к п. 3, если не выполняется, останавливаем счет и считаем х корнем.

Пример. Используя данше программы 4.11, при в=1-10" получим х== 1,171229661 при hRiA с.

§ 4.4. Решение систем нелинейных уравнений

Решение систем нелинейных уравнений может выполняться описанными выше методами, применяемыми поочередно к каждсму из уравнений системы с контрапем погрешности схождения каждой переменной к корню с заданной погрешностью. Останови.мся на описании двух модификаций метода итераций.

Решение системы нелинейных уравнений МЁТодом простых итераций зчключается в реализации итерациоииого процесса по следующей форму.ае:

(4.15)

применяемой после преобразования систем-Ы нелинейных уравнений общего вида

ад) = 0 (4.16)

к виду Xi=li{Xi). Здесь i - номер переменной (1, 2 Л/), п-номер йтереции. Вычисления ведутся до тех пор, пока соблюдается условие A,(„i> е, где s - заданная точность.

Метод Зейделя отличается от метода простых итераций тем, что уточненные