мы 4.22, реализующей этот метод, вводятся; ReZ(l)=-2,67949-!0~

степень полинома n = N, погрешность равен- ReZ(2)=- 2,00000

CTsa нулю-производной £1, погрешность вы- ReZ(3)=-3.73205

числения корней е = £2 и массив действи- ReZ(4)== -1,00000

тельиых а, и мнимых 6, частей коэффициен- ReZ(5)== - КООООО

тов Ai. Если Л,=а,-- действительные числа, ImZ(l)= -7 °6О"0 10" Л(1) = 1

Программа 4.24. ImZ(3)=-4,61.589.10" /С(3)=1

Пример. Решить уравнение lmZ(4) = 3,00000 К(4) = 1

Z + 8Z + 31Z + 802 + 942 + 20 = 0. ImZ(5)=-3,00000 Л:5)=1

Вводим N=5, an=i, ai=8, а2 = 31, Оз = 80, Значения K(i] хкззывают на кратность

а4 = 94, 05 = 20 и 6o-fc5 = 0. Результат полу- /-го корня. Для hr>/{]), ImZ{2) и !ni2(3)

чаем (при £1 = Ы0~ и £2=1-10") значения меньше заданной погрешности £2,

с округлением на пятой цифре: поэтому их следует считать нулевыми. Таки.м

Программа 4.24.

65 PRINTВЫЧИСЛЕНИЕ КОРНЕЙ ПОЛИНОИА P<Z>

10 PRINTC КОИПЛЕКСНЫИИ КОЭИЦИЕНТАИИ

15. INPUTЗАДАЙТЕ СТЕПЕНЬ ПОЛИНОИА N= N!LETH=n

20 DIM C<N+l),D<H+l),E<H+l)i.F<N+l)»61<N+l>

25 DIM A<H+l),BCN+l)»Fl<N+l),K<N),IlKN),ZKH)

36 LETX0=0!LETV0=0: INPUTВВЕДИТЕ Е1,Ё2 ЕЬЕ2

40 FOR 1=1 TO N+1!PRINT!2.в!ВВЕДИТЕ A<1-1>,Б<I-l)

50 INPUT ACI>,B<I>!HEXT l!LETIl=l

120 LEri«;=X0!LETV=V0sLETS=lJFOR 1=1 TO N+1

140 LETF<I>=A<I)!LET6Un=Ba)!LETC<I)=Aa)5l.ETDa)=B<I)

150 NEXT IiLETM=H!60T0 500

170 LETU1=U!LETU1=U:LETL=1S60T0 670

190 FOR 1=1 TO N+L-1

200 LETF(I)=C<I)!LET61<I)=Iia>:NEXT I 220 LET M=N-L!LETS=2S6OTO660 230 IF S0R<U"2+U2)>=E1 THEN 260 240 LETL=L+1!60T0 676

266 LET ги-г+и-г

276 LET 6=-<Ul3iiU+Ul*.y)Z

280 LETf)J=(UliKy-Ul*U)/Zs LETZ=SQRC&iKG+b.): LETUSl=b.Z 360 IF ABS(HZ>>1 THEN LETWl=Sl&N<f)JZ) 310 LETF2=ASN(f)Jl)L

326 IF 6<=6 THEN LETF2=«PI/L~ASN<W1)L 330 LETг=EXP<L0б<Z)/г)sLETб=ZжC0S<F2) 340 LETf)J=SKSIH<F2)sLETT=l!LETS=35LETM=H 356 FOR 1=1 TO N+1

360 LETF<I>=ft<I):LET&l<I>=B<I>sNEXT I

376 LETX=X0+Tiii6sLETV=V0+T*.Wi6OTO 606

396 IF <U2+U-2)<<U1"2+U12>THEN 485

406 LETT=T2S60T0376

410 IF Тж80Р<&г+Ы2)<Е2 THEN 468

426 LETX6=X:LETV0=V5LETS=1!FOR 1=1 TO N+1

440 LETC<I>=A<I)sLETBa)=Ba)!NEXT isBOTO 178

468 LETKai)=L!LETDiai)=X!LETZiai)=V

470 FOR J=l TO L!LETQ=N-J+ls&OTO 788

500 FOR 1=1 TO.QsLETA<I)=E<:i):LETB(I)=Fia)!HEXT IsHEXT J

520 IF N-L<=8 THEN 568

530 LETIl=Il+lsLETN=N-l!&OTO 120

560 FOR 1=1 TO H

578 PRINT!2.6!RE ZC I>=!F1.5!Iii<I) !2.8! IM I>=!F1.5!Z1(I> 5S0 PRINT!2.8!K<I)=K<n!NEXT I:STOE 680 LETU=F<n:LETy=61<l) 616 FOR 1=2 TO И+1

628 LETZ=UiKX-y!«V+FCD!LET U=UiKV+y!*X+&l<:i)sLETU=Z 640 NEXT I г IF S=l 60T0 178 . .

650 IF S=2 &0T0 230 660 &0T0 390 670 FOR 1=1 TO И

680 LETC<I)=ai-I + n*.C<I>!LETDa)=<M--l+l)*Iia)

698 NEXT I! &0T0 190

780 LETEa>=ft<:i)!LETFUl>=B<:i>

710 FOR 1=2 TO Q

728 LETEU>=A(I)+E<I-l )*X-F1 (I-l)i*V • 738 LETFl<I>=B(I)+E<I-l>i*V+Fl<I-l)iKX • 748 NEXT liBOTO 588:END

образом, уравнение имеет три действительных корня Z, = -0,267949, 2=-2 и 2з = = -3,73205 и два комплексно сопряженных 4.5= - !±/-3. Время счета контрольного примера около J0 мин.

§4.6. Поиск экстремумов функций одной и множества переменных

На практике часто необходимо найти экстремум (или экстре.чумы) некоторой целевой функции F{xi, Х2, Хп) п. переменных Xi (проектных параметре в). Такая функция описывает (n-f-1) мерную поверхность. Соответственно функция (л) одного параметра Х\ -X описывает некоторую кривую на плоскости (рис. 4-7, а). Поиск экстремумов функций одной переменной является само-стояте.пьной и часто встречаемой задачей. Кроме того, к нему сводится гораздо более сложная задача поиска экстремумов функций множества переменных (3, 41].

В общем случае функция F{x) может иметь несколько экстремумов (максимумов или минимумов). Из них главный (оптимальное решение для пространства проектирования) называется глобальным. Задача поиска экстремумов сводится к их локализации и уточнению значений х и /"(лг) в точке экстремума. В да-ньнейшем д.пя функций одной переменной под экстремумом будем подразумевать максимум F{x\ Поскольку максимуму функции F{x) соответствует минимум функции - F{x), то, сменив знак у f(x),. программами поиска максимума можно пользоваться и для поиска минимума функций. Будем также полагать, что на изменения х (если это особо не оговорено) накладываются ограничения в виде неравенств oxfc, где о и 6 - границы интервала поиска. В пределах отрезка [о, Ь\ функцию считаем унимодальной, т. е. содержащей один максимум (рис. 4.7,6).

Метой равномерного поиска основан на том, что переменной х присваиваются значения х + Ах с шагом Ax = const и вычисляются значения F{x). Если F{x„+\)> F(,x„), переменной X дается новое приращение. Как только F(x„+t) станет меньше F{x„), поиск останавливается. При малой заданной погрешности этот метод неэкономичен по затратам машинного времени.

Метод поразрядного приближения является разновидностью метода равномерного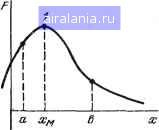

Рис. 4.7. Функция с несколькими экстремумами (п) и унимодальная функция с одним экстремумом максимумом (б)

поиска и реализуется следующим алгоритмом.

1. Задаем начальное приближение х=хо слева от максимума F(x) и вычисляем F{xd). Задаем D = h, где h=Ax - начальный шаг поиска.

2. Полагаем G = f(x„), где вначале f(>:„)= = F{xo), задаем x=x + D и вычисляем F(x„+,) = F{x).

3. Проверяем условие f(x„+i)> G; если оно выполняется, идем к п. 3, если нет - к п. 4.

4. Полагаем D=-D/4. Проверяем условие D>£/4, где £ -заданная погрешность вычисления х„ в точке максимума. Если оно выполняется, идем к п. 2, т. е. обеспечиваем поиск максимума в другом направлении с шагом в 4 раза меньше прежнего. Если данное условие выполняется, заканчиваем счет.

Программа 4.25.

16 PRINTпоиск максимума F<X> методом

15 PRINT поразрядного приближения

ге INPUTвведите начальный шаг поиска н= н

25 INPUTзадайте погрешность результата е= е

30 INPUTзадайте начальное значение X Х&= X

35 LETD=H:60SUB 86

40 LETCF!LETX=X+Ii! GOSUB 80

50 IF F>& THEN 40

•60 LETI)=-B/4: IF ABS<Ii)>E4 THEN 40 70 PRINTXM=X!PRINTF<XM>=Fs STOP 80 LETF=< <.1жХ-2>жХ+10)жХ 90 RETURN:END

Пример. Найти максимум функции

fM = 0,lx-2x+!0x. (4.22)

Подпрограмма вычисления F{x) записана со строки 80. Задав /г=1, £ = 0,001 и хп = 2, получим Хт = 3,33203125 и f (Х„) = 14,81481312.

Метод дихотомии (деления интервала поиска [а, Ь] пополам) реализуется следующим алгоритмом.

1. Проверяем условие Ifo -а<:2£, где £ - заданная погрешность вычисления jc„. Если это условие выполняется, идем к п. 6; если не выполняется, идем к п. 2.

2. Делим интервал поиска [а, Ь] пополам и вычисляем две абсциссы, симметрично расположенные относительно точки х = = {а + Ь)/2: х, = {а + Ь-г)/2к Х2={а + Ь + + е)/2.

3. Для этих значений х вычисляем F{x\) и £(X2).

4. Проверяем условие £(xi)> f(x2). Если оно выполняется, полагаем 6 = Х2 и идем к п. 1. Если не выполняется, идем к п. 5.

5. Полагаем a = xi и идем к п. !.

6. Выводим на печать х:„=(а+6)/2 и вычисляем F{х„).

Программа 4.26.

(см. алгоритм ниже). Ои позволяет сужать отрезок [а, Ь], каждый раз вычисляя лишь одно значение F{x), а не два, как в методе дихотомии. Данный метод реализуется следующим алгоритмом.

1. Находим коэффициент дробления k - ={ф-\)/2 отрезка [а. Ь].

2. Находим абсциссу xi = а+(1-ft) (6 -а) и вычисляем £ (xi).

3. Находим абсциссу X2 = a-\-k(b - a) и вычисляем £(Х2).

4. Проверяем выполнение условия Х2-xi<;£, где £ -заданная погрешность вычисления х„. Если это условие выполняется, вычисляем x„=(xi+X2)/2 и F{x„), после чего останавливаем счет с выдачей значений Хт и £ (х). Если данное условие не выполняется, идем к п. 5.

5. Проверяем условие £(xi)<£(x2). Если оно выполняется, полагаем a=xi, xi=x2 и £(xi) = £(x2), после чего выполняем п. 3 и п. 4.

6. Если £(xi)£(x2), полагаем 6 = Х2, Х2 = Х, f(xi) = flx,), после чего выполняем п. 2 и п. 4.

Программа 4.27.

Пример. Со строки 180 записана подпрограмма вычисления £(х)- для функции

Ш PRINTПОИСК МАКСИМУМА FOO МЕТОДОМ Д№ОТОМИИ

20 INPUTВВЕДИТЕ ГРАНИЦЫ ИНТЕРВАЛА ПОИСКА А,ВА,В

25 INPUTЗАДАЙТЕ ПОГРЕШНОСТЬ РЕЗУЛЬТАТА Е=Е

30 IF ABS(B-A><2*.E THEN lee

40 LETC= ч A+B~E > /-2! LETIl= (A+B+E > /-2

50 LETX=C:GOSUB 1£0:LETK=F

60 LETX=B!C<iSUB 126!LETL=F

70 IF K>L THEN Э6

80 LETA=C! GOTO 38

Э6 LETB=D: GOTO 38-

100 LETX=<A+B)-2! GOSUB 126

118 PRINTXM=X!PRINTF<XM)=F:STOP

120 LETF=<:<.1*X-2>*X+18)!«X

138 RETURN! END

Пример. Co строки 120 записана подпрограмма поиска максимума функции £(х) по формуле (4.22). При а = 2, 6=5 и £ = 0,001 получим х„ = 3,333429565 и £(х„)= 14,81481481.

Метод золотого сечения основан на делении отрезка [а, Ь] по правилу золотого сечения

(4.22). Для о = 2, 6 = 5 и £ = 0,001 получим х„ = 3,33495386 и £ (х„) = 14,81481479.

Метод квадратичной интерполяции - экстраполяции заключается в замене F{x) в промежутке Xi +h, где xi - начальное приближение, квадратической параболой, экстре-

Программа 4.27.

18 PRINTПОИСК МАКСИМУМА FCX) МЕТОДОМ ЗОЛОТОГО СЕЧЕНИЯ

20 INPUTВВЕДИТЕ ПРЕДЕЛЫ ИЗМЕНЕНИЯ X А,В .А,В

25 INPUTЗАДАЙТЕ ПОГРЕШНОСТЬ РЕЗУЛЬТАТА Е= Е

30 LETK=<;SQRi;5)-l V2

40 GOSUB 148

58 GOSLe 160

60 IF ABStD-CXE THEN 128 70 IF L>M THEN 108 88 LETA=C:LETC=D!LETL=M эе GOSUB 160:GOTO 68

180 LETB=D:LETD=C!LETM=L

lie GOSUB 148!GOTO 68

128 LETX=i:C+DV2!PRINTXM=X

138 GOSUB 188!PRINTF(XM>=F!STOP

148 LETC=A+a-K>*CB-A>

150 LETX=C!GOSUB 180:LETL=F:RETURN

168 LETIi=A+K!««:B-A>

170 LETX=D!60SUE 188:LETM=F!RETURN

188 LETF= a.1*X-2)«X+18 > жХ

1Эе RETURN!END