мум которой вычисляется аналитически. После приближенного нахождения экстремума Хт (максимума или минимума) можно задать xi=x„ и повторить поиск. Таким образом, с помощью итерационной процедуры значение Хт уточняется до получения его с заданной погрешностью е. Как видно из рис. 4.8, этот метод обеспечивает поиск как максимумов, так и минимумов f(x), в том числе для случая F (х) =0, причем точка Хт может лежать в интервале л1±Л (интерполяция) и быть вне его (экстраполяция); Алгоритм реализации этого метода следующий.

1. Задаем начальное приближение ,vi для Хм и вычисляем два смежных значения аргумента f(x):xo = Xi-h и X2 = xi+A, где А - полуинтервал интерполяции - экстраполяции.

2. Вычисляем три значения F (х): F (хп) = = Fo, F(x,)=f, и F{X2)=F2.

3. Находим коэффициенты

Fn F, , F2 1 (.,, 2f, + f,),

- f 1,(2X1 + A) + 4FiXi - F2(2xi - A)

параболы y[x)=x + bx + c, проходящей через выбранные три узла интерполяции - экстраполяции F(x), и по ним вычисляем аналитически положение экстремума

Хт = -

1 /-„(2X1 -bA) + 4F.v:i + F2(2xi - А) . ~2 F„-2F,-bF2

4. Проверяем выполнение условия (х,„ -xi) <е. Если оно не выполняется, задаем ,vi=Jf,„ и идем к п. ). Если выполняется, считаем Хщ найденным с заданной погрешностью е, вычисляем F (хт) и останавливаем счет.

Программа 4.28.

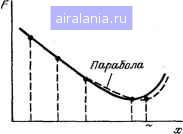Phc. 4.8. riuiicK экстремумо» максимума (u) и минимума (в) методом квадратичной И11те)-по.<1яиии - зкстраполяции

причем В обоих случаях экстремумы находились за преде.пами интервала xi+h.

Сравнение методов одномерной оптимизации показывает, что для простой функции F(x). например вида (4.22), они обеспечивают примерно одинаковое время поисйа (около 10 с). Исключением является последний метод, имеющий время поиска примерно в 2,5 раза 1у1еньше. Последнее связано с тем, что функция (4.22) близка к квадратичной параболе из-за малости коэффициента при х.

10-PRINTВЫЧИСЛЕНИЕ ЭКСТРЕМУМОВ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

20 PRINTМЕТОДОМ КВАДРАТИЧНОЙ ИНТЕРПОЛЯЦИИ-ЭКСТРАПОЛЯЦИИ

100 INPUTВВЕДИТЕ ШАГ Н=Н

105 1НРиТВВЕДИТЕ НАЧАЛЬНОЕ ЗНАЧЕНИЕ X1=Z

110 1НРиТЗАДАйТЕ ПОГРЕШНОСТЬ РЕЗУЛЬТАТА Е=Е

115 LETX=Z!60SUB 20e!LETU=F

120 LETX=Z-H!60StiB 200!LETU=F

130 LETX=Z+H!60SUB 2e6!LETU=F

140 ЬЕТТ=Ыж(2жг+Н)-4жи*г+иж С2жг-Н)

150 ЬЕТТ=Т<Ы~2жи+и)/-2

160 IF AES<T-2)<E THEN 180 • .

170 LETZ>=T!60T0 115

180 PRINTXM=T

190 PRINTF<XM)=U!STOP

200 LETF=< <.1жХ~2>жх+10>жХ

210 RETURNSEND

Пример. Вычисление F{x) для функции (4.22) производится, подпрограммой, записанной со строки 200. Для А = 0,1; xi=3 и е = 0,001 получим х„, = 3,33383342 и F (х„0 = = 14,8148146, а для X=8 х„, = 9,999499962 и F(a:„,) =2,414881321-10-. Уначения F (х,„) показывают, что в первом случае обнаружен максимум F(x), а вр втором - минимум.

В большинстве саучаев для гладких F(x). метод квадратичной интерполяции - экстра поляции дает заметный выигрыш во времени вычислений. Удобно и то, что он без всякой перестройки программ обнаруживает как максимумы, так и минимумы F(x), причем даже за пределами первоначально заданного интервала поиска. Преимущество метода

золотого сечения перед методами поразрядного приближения и дихотомии при простых F{x) ие выявляется, поскольку программная реализация первого метода сложнее и необходимо выполнение ряда вспомогательных операций. Однако при сложных F(x) метод золотого сечения может давать существенный выигрыщ во времени. Для поиска экстремумов пользуются также методом с числами Фибоначчи [3, 41], однако особым преимуществом перед методом золотого сечения он ие обладает.

Многомерная оптимизация заключается в поиске экстремумов функции многих переменных F(X], Х2.....Хп). Методы такой оптимизации детально описаны в [3, 38, 41]. Из всего многообразия методов многомерной оптимизации ограничимся рассмотрением трех относительно простых методов поиска минимума F{Xi, Хг, .... х„).

Метод координатного спуска заключается в поочередном поиске минимума по координате Xi, затем xi и т. д. После нахождения точки минимума по координате Xt переходим к нахождению точки минимума по Координате Х2 и т. д. Поиск ведется с одинаковым шагом, который уменьшается после нахождения всех значений Xim, Х2т.....х„„. Таким

образом, алгоритм реализации этого метода подобен алгоритму метода поразрядного приближения и лишь дополняется циклом задания переменных Xi, X2, х„, внутри которого оценивается погрешность нахождения хш для каждой переменной.

Программа 4.29.

Метод спирального координатного спуска отличается от рассмотренного выше лишь тем, что шаг Я меняется каждый раз при переходе от поиска минимума по одной переменной к поиску минимума по другой переменной. В трехмерном пространстве это напоминает спуск во впадину по спирали. Обычно этот метод дает некоторое сокращение времени поиска.

Программа 4.30.

Со строки 120 записана подпрофамма вычисления функции (4.23). Для xio=a:2o- =Хзо = 0,5; Я=0,5 и £=-Ы0~* получим х,„= 1,000032; X2„=2,000032; хз«,«3,000032 и F (Xi)„„„=t= 3,735451795 при <с»1,5 мни.

Метод координатного спуска с квадратичной интерполяцией - экстраполяцией основан на последовательном поиске минимума каждой переменной с применением для этого метода квадратичной интерполяции-экстраполяции.

Программа 4.31.

Пример. Со строки 250 записана подпрограмма вычисления функции (4.23). При Я=0,01; £=Ы0-*; xio=X2o=X3o=0,5 получим x,„= 1,000033409; Х2и = 2,000016758; Хз™ = 3,000008996 и F (х,) „„„=3,735514058

(/с»1 мин).

Применение многомерной оптимизации для решения систем уравнений (линейных и нелинейных). Если дана система уравнений

fi{xi, Х2.....х„)=0,

МХ, Х2, х„) = 0,

fn(X,, Х2, х„) = 0.

10 PRINTМИНИМИЗАЦИЯ ФУНКЦИЙ N ПЕРЕМЕННЫХ МЕТОДОМ 15 PRINT КООРДИНАТНОГО СПУСКА

28 INPUTЗАДАЙТЕ ЧИСЛО ПЕРЕМЕННЫХ N=N!liIM ЙСЮ 25 1НРиТЗАДАйТЕ НАЧАЛЬНЫЙ ШАГ ПОИСКА H=H!LETL=H 38 INPUTЗАДАЙТЕ ТОЧНОСТЬ РЕЗУЛЬТАТА Е=Е

35 FOR 1=1 ТО N .

48 PRINT!2.8!ВВЕДИТЕ НАЧАЛЬНЫЕ Х1 8=

45 INPUT A<I>:NEXT I

58 FOR 1=1 TO H!LETB=.9E98

68 LETAa>=Aa)+H:60SUE 15e!LETC=B!LETB=F

?B IF F-C<e THEN 68

88 LETH=-H--3! IF ABStH) >=AESa3> THEN 68

98 LETH=L!NEXT I

188 LETL=L>9:LETH=L

lie IF E-9<=L THEN 58

115 PRINT!F1.9IF(XI MIN>=F

128 FOR 1=1 TO N

138 PRINTI2.8!XI MIN=!F1.9!A(I> 135 NEXT ISPRINTКОНЕЦ ВЫЧИСЛЕНИЙsSTOP 148 NEXT ISPRINTКОНЕЦ ВЫЧИСЛЕНИЙ:STOP

158 1ЕТР=ехр1:Аа>+А2)+а1:з>>.ЧАа>жА<;2>жА<:г>жА«:з>жА<з>жА«:з>>

168 RETURNS END

Пример. Co строки 150 записана подпрограмма вычисления функции

ехр(Х+Хг-Ьхз)

F(Xl, Х2, хз) =

<1X2X3

трех переменных. Для начальных значений Х1о=Х2о=Хзо = 0,5, шага Я=0,5 и погрешности £=Ы0- получим Xi„=0,9999745973; Х2„= 1,999974597; Хз = 2,999979597 и F (х,)„„„ = 3,735451794.

Время счета около 1,5 мин.

то поиск минимума функций

(4.23) £(*,)= или £(х.)= (to))=

дает неизвестные этой системы.

Пример. Найти неизвестные системы из двух нелинейных уравнений

х?+Х2 = 1;- X?-Х2=0.

Численное дифференцирование аналити- ч„2 Лп 1 ч„2 9„ 2

чески или таблично заданной функции у{х) -t---:t--y,.,--2L----,

заключается в замене у{х) интерполяцион- 2 2

ным полиномом Я(х), производные (ГР{х)/dx" ~ 2 j

~d"y{x)/dx" которого можно найти анали- -\-L--у],

тически с помощью соответствующих фор- 6 /

Я PRIWrминимизация функций Н переменных методам

15 print спирального координатного спуска

ге inputзадайте число переменных N=N:BIM A(N>

£5 inputзадайте начальный ШАГ поиска н=н

зе inputзадайте точность результата е=е

35 for 1=1 то n

40 print!2.о!введите начальные х1 0=

45 input a<i>!next i

50 FOR 1=1 to N:LETB=.9E9S

60 LETAa>=a<i>+h!gosub 12e!LETC=b:letb=f

70 if f-C<e then 60

75 next i

80 leth=-h5: if abs<h>>e/5 then 50 90 print!f1.9!f<xi min>=f 100 for 1=1 to n

110 print!2.0!xi min=!f1.9<Aa) 115 next i!printkoheц вычисленийsstop

120 ьетр=ехр<а<1)+а*:2>+а<:з>)*:а<1>жа(2)!«а<2>*а(з>жа*:з)*.а(з>) 130 return! end

Программа 4.31. •

10 printминимизация функций N переменных fcxij методой 15 print квадратичной интерполяции-экстраполяции 20 inputзадайте число переменных n=n:dim acn> 25 inputзадайте погрешность вычисления е=е - 30 inputзадайте интервал интерполяции н=н 35 for: 1=1 то n

40 print!2.0!введите начальные значения х1нач=

50 input a<i)!next i

100 LETS=0

110 for 1=1 to n

120 letz=aci>!&osub 250!letu=f

130 leta<i)=2-h!60sub 250!letw=f

140 l£TAa)=z+h!gosub £50!letu=f .

150 LETT=t05«<:£i*z+h>-4*.U*z+UiK<:2*.z-h> 160 lett=T/a.l-2iKU+u>/2

170 if abs<:t-z>>e then LETS=1

180 leta<i>=t!next i

190 if s<>0 then 108

200 print!f1.9!f<;xi min>=f

210 for 1=1 TO N

££0 print«£.6!xtmih=!f1.9! Atl) £30 next i

240 printконец вычислений:stop

250 letf=exp<Ai: 1 )+a(2j+a«:3)VtAt 1 ?жА«:2>*а(2?жА«:3>жА«::)жА«:3>> 260 return:end

Для них имеем мул. Для функций, заданных таблично со

р. , 2 1 „2 n2i /„3 л2 случайной погрешностью, точность чис-

t(xu X2) - {x,-t-X2 i; -t- 1 2; ленного дифференцирования может быть

Воспользовавшись программой 4.31 при низкой. , . .

Я = 0 01- £=1-10 и xi() = X2o=l, получим Численное оидхреренцирование при равно-

х,. = 0,8259; Х2„=0,563б и £ (х,„,. Х2„,) = расположенных узлах с интерполя-

= 2,2726-10-Г Подстановка и в исход- реализуется следующими формулами

ные уравнения дает xL+>:„, = 0,9998~ 1 и (m« 3, 4 и о узлов):

х m - Хг™ = - 2 -10 - * ~ 0. у(х„ + phh =

§ 4.7. Численное =Кр-о,5).у ,-2р.уп+(р--0,5)у,],

дифференцирование и вычисление

коэффициентов чувствительности j;(xn-i-p/i).=-/- р-р+