10 PRINTВЫЧИСЛЕНИЕ ТРЕХ ЧАСТНЫХ ПРОИЗВОДНЫХ И

20 PRINTОТНОСИТЕЛЬНОГО КОЭФФИЦИЕНТА ЧУВСТВИТЕЛЬНОСТИ

30 PRINTФУНКЦИИ PiCXI) РЯДА HEPEMEHHfclX, ЗАДАННОЙ

40 PRINTAHAЛИТгЧЕСКИ-ПОДПРОГРАМГЧА СО СТРОКИ 400

50 INPUTВВЕДИТЕ ЧИСЛО ПЕРЕМЕННЫХ N=N

60 DIM X<N),A<N),B<:N)/C<N)/S<N)!F0R 1=1 ТО н

70 PRINT!2.0!ВВЕДИТЕ НАЧАЛЬНОЕ ЗНАЧЕНИЕ Х*;1> .

80 INPUT Х<П! NEXT I

90 INPUTЗАДАЙТЕ АВСОЛНПНОЕ ПРИРАШЕНИЕ Х<1) Н=Н

100 FOR 1=1 ТО N!LETX(0>=X<I)

110 ЬЕТХ<1>=Х<0)-ЗжН!бО8иВ 400!LETF3=F

120 CnOSUB 400!LETF2=F:GOSUB 400:LETF1=F!GOSUB 4ee!LETEe=F

130 C<iSUB 400!LETE1=F!GOSUB 400!LETE2=F!GOSUB 400!LETE3=F

140 LETA<I)=<ЕЗ-9жЁ2+45жЕ 1 -45!*F 1 +9жРг-Р3)SeH

150 LETB<I>=2жЕЗ-г7жЕ2+270жЕ1-490жЕ0

160 LETB< I)=< В a ) +270*F 1 -27жР2+2жРЗ ) >-180>-Ч НжН )

170 ЬЕТС<1)=<8жЕ2-ЕЗ-13жЕ1+13жр1-8жР2+РЗ)-8>-ЧН"3)

188 LETS<I>=A<I)«X<0)/E0!LETX<I)=XC0)!NEXT I

200 FOR 1=1 TO N!PRINT!2,0ДЛЯ ПЕРЕМЕННОЙ XCI)

210 PRINT!F1.9!D1F>-DX1=A<I)

220 PRINTD2F/IiX2=B< I >!PRINTr3F/-DX3=CiI)

230 PRINTS=S<I)!NEXT I

240 PRINTЗНАЧЕНИЕ ФУНКЦИИ F<X105=E0!GOTO 98 400 LETF=EXP(-XCl)"2/2)>-SG!R<2!t;#Pl) 410 L£TX<;i)=X<I)+H!RETURN!END

Работу этой программы также можно проверить по приведенному выше примеру. Следует отметить, что из-за ошибок округления точность численного дифференцирования при малых hup при 7 точках улучшается незначительно, а иногда даже ухудшается (в сравнении с дифференцированием по 5 точкам).

§4.8. Вычисление определенных интегралов

Определенный интеграл ь

(4-.25)

с пределами интегрирования о и 6 можно трактовать как площадь фигуры (рис. 4.9), ограниченной ординатами о и 6, осью абсцисс X и графиком подынтегральной функции f(x).

Поэтому, достаточно вычислить значения функции F{x). Большое количество определенных интегралов приведено в книге [30].

Численное интегрирование применяется, если нахождение F(x) сложно или невозможно. Оно заключается в интерполяции fix) на отрезке [а, 6] подходящим полиномом, для которого определенный интеграл вычисляется по формулам численного интегрирования. Обычно отрезок [о, 6] разбивается на m частей, к каждой из которых применяется соответствующая простая формула. Таким образом получают составные (или сложные) формулы численного интегрирования.

Метод прямоугольников - простейший прием численного интегрирования, при котором функция у -fix) заменяется интерполяционным многочленом нулевого порядка. Для повышения точности интегрирования отрезок [а, Ь] разбивается на m частей и формула прямоугольника применяется к каждому отрезку. Пр.чведем обобщенную формулу прямоугольников:

в х

Рнс. 4.9. Графическая иллюстрация численного интегрирования

Обыкновенный определенный интеграл, у которого известна его первообразная F{x), вычисляется по формуле Ньютона - Лейбница

I = F(b)-Fia).

Вследствие низкой точности этот метод почти не применяется.

Модифицированный метод прямоугольников базируется на представлении f{x) ординатами, смещенными ня величину 0,5ft, где h = (b - a)/m:

IhY fiM5h)+-f%),

1 = 0

"Де /"(I) - значение второй рроизводной f{x) в точке лг = 5, где она максимальна.

Метод трапеций заключается в линейной аппроксимации f{x) на отрезке [а, Ь]. Для уменьшения погрешности [о, Ь] pa;бивaeтcя

на m частей длины h={b - a)/m (при методе прямоугольников /(x,)=const = y, на этом отрезке).

С учетом суммирования смежных ординат внутри отрезка [а, Ь] обобщенная формула метода трапеций имеет вид

в связи с легкостью программной реализации и низкой точностью рассмотренных методов программы для них не приводятся.

Метод Ньютона - Котеса основан на интерполяции f{x) в п промежутках полиномом Лагранжа. В общем случае f{x) должна задаваться (п + 1) ординатами. Формулы интегрирования точны, если / (лг) - многочлен п-й степени. "При п=1 получаем метод трапеций.

Метод Симпсона (парабол) - частный случай метода Ньютона - Котеса при п = 2. При разбиении отрезка [а, Ь] на т равных отрезков получим обобщенную формулу Симпсона

/ = \ Цх) dx~- \Ца) + 4Ца + h) + 2f(a + 2h) +

+ 4Ko + 3ft) + ...+4/(fc-ft)+/(fc)]-/(g)

Выражение для остаточного члена показывает, что формула Симпсона точна, даже если fix) - многочлен третьей степени. Эта частная особенность формулы Симпсона объясняет ее преимущественное применение - у некоторых ЭВМ вычисление по ней реализовано микропрограммно.

Алгоритм реализации метода Симпсона дан на рис. 4.10.

Программа 4.37.

Пример. Вычислить интеграл 1

(4.26)

/=\ V2x-f I djr= 1,398717474

при 0 = 0 и Ь = \. Вычисление подынтегральной функции оформляется подпрограммой - см. строку 110. Для /и = М = 8 получим /=1,39871724 при /,»5 с.

Программа 4.37.

Пуси J

/ввод А,В / Обращение к подпрограмме / Вычисления f(X)

/ ВвоВМ /

И=(В-А)1М12 Х=А

I=F,N=0

N=N~2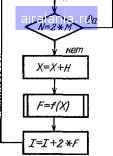

I=(l+F)*H/3

№неи,

Рис. 4.10. Алгоритм численного интегрирования по составной формуле Симпсона

Интегрирование по формуле Бодэ 1= \ I{x)dx=~(7y, + 32yi + l2y2 +

+ 323 + 74/.)-8Г(у

10 PRINT ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ МЕТОДОМ СИМПСОНА

28 INPUT ВВЕДИТЕ НИШНИЙ ПРЕДЕЛ ИНТЕГРИРОВАНИЯ А=А

25 INPUT ВВЕДИТЕ ВЕРХНИЙ ПРЕДЕЛ ИНТЕГРИРОВАНИЯ В=В

30 INPUT ВВЕДИТЕ ЧИСЛО ИНТЕРВАЛОВ ИНТЕГРИРОВАНИЯ М=М

40 LET Н=<В-А)/М/2 : LET Х=А

50 60SUB 110 ! LET I=F s LET N=0

60 LET X=X+H ! GOSUB 110 : LET I=I+4*F

70 LET N=N+2 ! IF N=2*M THEN 90

80 LET X=X+H ! GOSUB 110 : LET I=I+2*F s GOTO 60 98 LET X=B : GOSUB 110 : LET I=<I+F)*H/3 95 PRINT ДЛЯ A=A B=B И M=M: PRINT" 188 PRINTЗНАЧЕНИЕ ИНТЕГРАЛА I=l!60T0 30 110 LET F=SQR<2*X+1) s RETURN s END

примененной к каждому из т отрезков разбиения [о, Ь], реализует следующая программа.

Программа 4.38.

по формуле, содержащей одинаковые множители bi = 2ln перед /{/;). Однако при этом абсциссы Ь располагаются неравномерно. Так, для п = 3 /, = --у/2/2, и = Ь и h=/2

10 PRINTЧИСЛЕННОЕ ЙНТЕГРИРОВйНИЕ ПО ФОРМУЛЕ БОДЭ 20 INPUTВВЕДИТЕ НИШНИй ПРЕДЕЛ ИНТЕГРИРОВАНИЯ А=А 30 INPUTВВЕДИТЕ ВЕРХНИЙ ПРЕДЕЛ ИНТЕГРИРОВАНИЯ В=В 40 INPUTВВЕДИТЕ ЧИСЛО ИНТЕРВАЛОВ ИНТЕГРОВАНИЯ М=М 50 LETH=<B-A>/M:LETE=H/4!LETX=A:60SUB 130!LETI=7*F 60 FOR N=1 ТО M!UETX=X+E 70 GOSUB 130!LETI=I+32*F:LETX=X+E 80 GOSUB 130!LETI=I+12*F:LETX=X+E 90 GOSUB 130:LETI=I+32«F:LETX=X+E

100 GOSUB 130:LETI=I+14«F . "

110 NEXT N

120 LETI=I-7*F!LETI=I*2*E/45

125 PR I NTЗНАЧЕНИЕ ИНТЕГРАЛА IUGOTO 40

130 LETF=SQR<2*X+1)!RETURN:END

Пример. Для интеграла (4.26) при m=4 получим /=1,398717463 при /с~5 с. Подпрограмма вычисления /(х) записывается со строки 130.

Метод Уэддля базируется на применении к каждому из m отрезков разбиения [о, Ь] формулы

/=5 /(x)rfx =

12700

Программа 4.39.

Пример. Для интеграла (4.26) при т = 4 получим /=1.398717474 при /с~5 с. Подпрограмма вычисления /(х) записывается со строки 170.

Формула Ньютона - Котеса с повышенной (в сравнении с формулой Уэддля) точностью для т = 6

(41;Ус-Ь216;У,-1-27;у2 +

/ = \Mx)rfx~-

+ 272уз + 27у4 + 216уб + 41ув) -

1400

реализована в следующей программе. Программа 4.40.

Пример. Для интеграла (4.26) при т=4 получим /=1,398717474 при /c»5 с. Подпрограмма вычисления /(х) записывается со строки 130.

Приведенные выше методы интегрирования имеют равномерное расположение абсцисс х„ для которых вычисляются i!/i = f(Xi). При этом крайние значения х; равны о и (за исключением модифицированного метода прямоугольников) .

Метод Чебышева основан на вычислении значения определенного интеграла

/= \ mt~-Y. m)h>Y т (4.27)

интеграл (4.27) приводится к виду (4.25) подстановкой

(4.28)

Формула (4.27) точна для полиномов степени п.

Программа 4.41.

Пример. Для интеграла (4.26) при т = 8 получим /=1,398717533 при 4» 6 с. Вычисление Дх) оформлено подпрограммой (строка 140).

Метод Гаусса основан на интерполяции /(х) полиномом Лагранжа, но абсцисры х, выбираются из условия обеспечения минимума погрешности интерполяции. При этом интеграл (4.25) подстановкой (4.28) сводится к виду

(4.29)

Метод Гаусса обычно обеспечивает повышенную точность - формула (4.29) верна для полиномов до (2п-1)-й степени. Для п = = 3 Л, =5/9, /, = -173, л2 = 8/9, /2 = 0, /1з = 5/9 й /., = -/Г/3. Остаточный член (погрешность) при этом равен

15750

Для повышения точности интегрирования отрезок [о, Ь] дробитря на т частей. Программа 4.42.

Пример. Для интеграла (4.26) при М = 8 получим /=1,398717474 при /с га 6 с. Подпрограмма вычисления f(x) записана со строки 130. При численном интегрировании с заданной точностью оценка погрешности интегрирования обычно сложна и требует вычисления высших производных f{x). Поэтому на практике принято проводить интегрирование для ряда т = 2, 4, 8 и т. д., считая верным число совпадающих первых цифр результата. Этот процесс легко автоматизировать, что положено в основу программы 4.43.