г л А в А 5

СПЕКТРАЛЬНЫЙ, СТАТИСТИЧЕСКИЙ. КОРРЕЛЯЦИОННЫЙ И РЕГРЕССИОННЫЙ АНАЛИЗ

§ 5.1. Спектральный анализ на основе дискретного преобразования Фурье

Спектром временной зависимости (функции) у (t) называется совокупность ее гармонических составляющих (гармоник), образующих ряд Фурье (см. § 4.11).

Спектральный анализ периодических функций заключается в нахождении коэффициентов Ок, Ьк ряда Фурье

у (0=-f+ у {akCos2nkfit + bksm 2nkf,t),

(5.1)

где /[ - частота повторения (или частота первой гармоники), k - номер гармоники. Кроме ряда (5.1) широко используется ряд

у (0=-f-+ J Мк cos {2nkfJ+ifk}, (5.2)

Mk=Mai + bl

(5.3)

- амплитуда и

Ф*=-arctg (fct/ut) (5.4)

- фаза гармоник (косинусоид). Применяются также ряды с синусоидами под знаком суммы.

Коэффициенты Фурье определяются выражениями т

ак=-[ у и) cos 2nkf,t. (5.5)

(5.6)

где T=l/f[ - период повторения периодической функции у (О-

Спектральный анализ непериодических {финитных) функций, т. е. функций, полностью определенных на отрезке [О, to], заключается в вычислении составляющих их комплексной спектральной плотности

S (/ш) =Sc (ш) + jSs (ш) =S (to) e-W,

bk=\y {П sm2nfa.

где (о = 2л/ - угловая частота,

S (w)=V[Sc (o))]4[Ss (0))]= (5.7)

Ф (о)) = -arctg [Ss (o))/Sc (о))] (5.8)

- модуль спектральной плотности и фаза на частоте м. При этом

•Sc=S У (О cos iot.

Ss=S у (О sin (йЛ

(5.9)

(5.10)

Численный спектральный анализ заключается в нахождении коэффициентов Оо, а.....

ok, bi, Ьу, bk (или Ml, М2.....Мк,

Ф1, ф(,) для периодической функции

y(t), заданной на отрезке [0,7"] дискретными отсчетами. Он сводится к вычислению (5.5) и (5.6) по формулам численного интегрирования для метода прямоугольников (см. § 4.8)

i<=~j;j- yiCos2nkf,i At,

.(5.11) (5.12)

.=0

где At = T/N-шаг, с которым расположены абсциссы у {t).

Для финитных функций

Sc = At X yicos {2nfAt[), (5.13)

Ss = At I/,-sin {2nfAtl).

i = 0

(5.14)

Найденные no (5.11) и (5.12) коэффициенты Фурье для m = N/2 гармоник приближают у (t) рядом (5.1) или (5.2) с наименьшей среднеквадратической погрешностью. Следовательно, численный спектральный анализ, совместно со спектральным синтезом (§ 4.11), является разновидностью метода наименьших квадратов, когда у {t) приближается тригонометрическим рядом.

обобщенный, численный спектральный анализ базируется на том, что периодические функции у (t) являются частными случаями финитных функций. Действительно, полагая ti] = T (этим мы условно приписываем финитным колебаниям период 7") и считая f=kf, (при финитных функциях k - любые, а при периодических - целые числа), из (5.11), (5.13) и (5.12), (5.14) получаем

с. N-i

a*N V „ел

У< cos 2я/ Д/,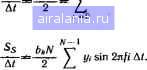

(5.15)

(5.16)

Численный спектральный анализ повышенной точности основан на априорном представлении у (t) в промежутках между узлами. Если такое представление невозможно, используются формулы (5.15) и (5.16), дающие наименьшую среднеквадратичную погрешность (рис. 5.1, а). Если г/(/) =const в промежутках между узлами (рис. 5.1,6),

Использование только ненулевых отсчетов позволяет уменьшить время анализа, если у [Т)=0 в начале или конце отрезка [0,7"] или [О,/п]. Однако отсчеты у,=0 при Л?1 М должны вводиться.

3. Задаем шаг Д/.

4. Переменным С и S присваиваем нулевое значение, организуем ввод частоты f и находим pnf Ы.

5. Находим Ло и Во с помощью цикла, в котором вычисляются

C = C+t/iCos (2ip), S = S-f(/isin (2ip),

где i - N\, yVl-f 1, M. При выходе из

цикла Лс=С и Во=С.

6. Для заданного значения f находим нужные параметры at, bt или Мк и (pt, Sq, Ss или S и ф. Например, для вычисления S и ф применяем формулы

фрад = С=-arccos (Ло/m) приВоО,

фрад=-С

при Вп<0.

(5.21)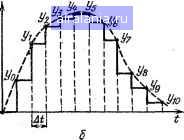

Рис. 5.1. Задание решетчатой (а) и ступенчатой (б) функция.чн

то можно получить для Ак, Вк точные значения Aki, Вк\, вычисляя их по формулам

-4*1=*0, Bki-KiBko, (5.17)

где Ki=i при f = 0,

Kf={s\nnf At)/nf М при /0. (5.18)

Формулы (5.17) с учетом Ki (5.18) получаются в результате аналитического интегрирования (5.5) и (5.6). Если в промежутках между узлами функция у (t) аппроксимируется линейной зависимостью, то уточненные значения А и В будут равны

Ak2 = KfAk«, Вк2 = фк«. (5.19)

Последовательный спектральный анализ на ЭВМ выполняется по следующему алгоритму.

1. Вводим N - число интервалов разбиения у (I). N1 - номер первого ненулевого отсчета у (t) и номер последнего ненулевого отсчета М.

2. Организуем цикл ввода ненулевых отсчетов у, с управляющей переменной /, меняющейся с шагом 1 от значения /VI до М.

Формулы (5.21) дают представление фрал в пределах ±л рад (или ±180°, если ф) рад умножить на множитель 180/л). С помощью (5.17) - (5.19) могут вычисляться уточненные значения А\, В\, S\-kfS и Лг, В2, Si - kfS при ступенчатой или кусочно-линейной аппроксимации у (/).

7. Возвращаемся к п. 4 и повторяем вычисления для нового значения частоты f.

Таким образом, последовательный спектральный анализ обеспечивает возможность вычисления амплитуды и фазы любой гармоники (или спектральной плотности на любой частоте). При этом необходимо запоминание всех отсчетов г/,, кроме нулевых в начале и в конце интервала дискретизации у (/). Число отсчетов ограничено емкостью ОЗУ ПЭВМ и достигает 100-250 у простых ПЭВМ. Из-за резкого увеличения времени вычислений (оно пропорционально Л) спектральный анализ описанным методом на ПЭВМ при большем числе отсчетов нецелесообразен.

05 PRINT ПОСПЕДОВЙТЕПЬНЫЙ СПЕКТРАЛЬНЫЙ ЙНЙЛНЗ

10 INPUT ВВЕДИТЕ ЧИСЛО ИНТЕРВАЛОВ РАЗБИЕНИЯ N=N

15 INPUT ВВЕДИТЕ НОМЕР ПЕРВОГО НЕНУЛЕВОГО ОТСЧЕТА N1=N1

£0 INPUT ВВЕДИТЕ НОМЕР ПОСЛЕДНЕГО НЕНУЛЕВОГО ОТСЧЕТА М=М

30 BIM VtMJsFOR I=N1 ТО М

35 PRINT!3.0!ВВЕДИТЕ ОТСЧЕТ V<: I>: INPUT Va> 40 NEXT I!INPUTЗАДАЙТЕ ШАГ Т=Т 50 INPUTВВЕДИТЕ ЧАСТОТУ F=F!LETC=0:LETS=0 60 иетр=#Р1жРжТ!ЬЕТЫ=гжр!Р0Р I=N1 ТО М

70 LETZWiKi! LETC=C+V<: I V*COS(Z)!LETS=S+V<:I >*SIHi:Z>!NEXT I

80 LETR=SGR<:C*C+S*S): LETF=-ACS(C/R>-#Pr*T*F

90 IF S<0 THEN LETF=-F

100 LETK=S IN CP ) /-P! LETR1 =K*R! LETR£=K*R 1

110 PRINTIF1.9lnPH РЕШЕТЧАТОЙ V<:T> Si:FJ=R*T

120 PRINTnph СТУПЕНЧАТОЙ VCT) S1<F>=R1*T

130 PRINTПРИ КУСОЧНО-ЛИНЕЙНОЙ V<TJ S2(F)=R2*T

140 PRINTФАЗОВЫЙ УГОЛ В РАДИАНАХ F=F

150 PRINTФАЗОВЫЙ УГОЛ В ГРАДУСАХ F=BE&(F)

160 GOTO 50!ENB

Пример. Найти спектральную плотность прямоугольного импульса, заданного

отсчетами г/о=1, i/i = l.....г/7=1 при Л/ = 32

и д/=0,125-10- с для частоты / = 250 ООО Гц. Вводим эти данные (Л/1=0, М = 7) и получаем So=9,01764195-10-; S, =9,003163162Х X10 (это значение полностью совпадает с теоретическим, поскольку для прямоугольного импульса ступенчатая аппроксимация у (i) является точной); 52 = 8,98870762-10- и фазовый сдвиг ф=-39,375°.

При интерпретации результатов вычисления фазового сдвига следует помнить о конечной области определения углов (в данном случае от -180° до -f 180°). Кроме того, надо учитывать, что значения аргумента у синусов и косинусов не должны выходить за пределы, допустимые для данной ПЭВМ (см. § 2.6). Из-за приближенности аппроксимации у (t) значения ф могут сильно отличаться от точных. Иногда это можно устранить, введя поправку для ф, равную дф= = л/д/ (в радианах) или дф=180/дг (в гра- , дусах). Так, в примере к программе 5.1 дф= 180-2,5-10-0,125-10 = 5,625°. При этом скорректированное значение угла

ф=-(39,375 + 5,625) = -45° равно точному значению.

Параллельный спектральный анализ на ЭВМ заключается в одновременном (параллельном) вычислении М гармоник. При этом память ЭВМ нужна для запоминания коэффициентов о*, bi, (или Ль В/,), однако запоминать все отсчеты г/, не требуется, поскольку каждый отсчет используется для вычисления всех гармоник по мере его ввода. Параллельный спектральный анализ проводится по следующему алгоритму.

1. Вводим нужное число гармоник М, номер начальной гармоники kS, общее число отсчетов у (<) N, номер первого ненулевого отсчета IS и номер последнего ненулевого отсчета IF.

2. Обнуляем переменные массивы Л {k) и В (k) и вычисляем R - 2n/N.

3. Организуем цикл ввода yi=Y с управляющей переменной /, меняющейся с шагом 1 от значения IS до IF. В этом цикле вво-

дим у,, вычисляем Z = Rl и организуем внутренний цикл (п. 4).-

4. Организуем цикл вычислений Л*, В/, с управляющей переменной k, меняющейся с шагом 1 от значения О до М-1. В начале цикла вычисляем li = Z (k + S), где S = IS, и затем

В {k)=B {k) + Ys\n W.

Значения Л* соответствуют переменным массива А [k), а Bt-переменным массива В {k) после выхода из циклов. Для нулевой гармоники fe + S = 0 вычисляем только Ло, суммируя все у/.

5. Организуем цикл вывода Л*, В,„ М/, и ф* = р(, (fe = 0, М-1), учитывая сдвиг индекса на величину S, т. е. вывода вместо индекса k значения k + S. В ходе вывода вычисляем

M + S

М2= Y.

i = k+S

6. Если М1=0, т. е. вычисления начаты с первой гармоники, находим коэффициент гармоники:

k, = M2 + Ml+ ... +М/М,=

=vm2-m?/m,.

7. Если 5=1, можно проводить тригонометрическую интерполяцию - экстраполяцию, т. е. по заданным / вычислять

J/(О =4+4( J cos 2лАг/д/ +

м

. . : + Bks\n2nkfAt

с помощью усеченного ряда Фурье, ограниченного М гармониками.

Когда по этому алгоритму надо вычислить новый ряд гармоник, приходится повторять