Случайные числа с нормальным распределением могут быть получены с помощью формул

/?/=л/21п (I/V,) cos (2яК ), /?r=V2ln sin (2яК 1).

При этом получается сопряжеин1Я пара чисел, имеющих среднее значение = 0 и среднеквадратичное отклонение о = 1. При других значениях R и о производится пересчет по формуле

Обобщенный алгоритм реализации метода Монте-Карло (рис. 5.3) обеспечивает моделирование работы объекта и вычисление основных статистических характеристик его функциональных параметров.

Наглядным примером применения метода Монте-Карло является программа 5.13 для обучения щкольников млэдщих классов таблице умножения. Программа генерирует два случайных числа, переводит их в отрезок [1;9] и предлагает учащемуся перемножить эти числа. Результат сравнивается с правильным. Оценка выставляется по результатам анализа десяти операций перемножения. Читателю предлагается самостоятельно разобрать эту программу.

Программа 5.15.

формирование слути.нь1х шсел-параметров с равномерным распределением

Лреодразодание законов распределения

Вы1/исление реакции. оБъента на случайные бозВейстВая-параметры

Статистическая оЬраБотка результатов

Рис. 5.3. Обобщенный алгоритм примеиеиня метода Моите-Карло

Корреляционный момент двух последовательностей

/?л.»=-д ({/. -"11») (А-.-m,,).

85 PRINT-ОБУЧЕНИЕ TftEfiHUE УМНОЖЕНИЯ

18 LETX=.7654321:LETN=8

20 FOR 1=1 TO 18

38 LET ft=RNIi<X>:LET B=RND<X)

40 LET ft=INT«:ft!«9+l>:LET E=INT<B*9+1)

58 PRINT!2.8!CK0flbK0 БУДЕТйжВ=?--s INPUT"C

68 LET D=ft*B! IF C=Ii THEN 88

70 PRINTHEBEPHO-ft!«B=Ii:LET N=N+l!&0T0 85

88 PRINTПРАВИЛЬНО

85 NE-XT I

98 IF N=0 THEN 148 .

188 IF N<=1 THEN 158 118 IF N<=3 THEN 160

128 PRINTВЫ HE ЗНАЕТЕ ТАБЛИЦУ УИНОМЕНИЯ

130 PR INTПОУПРАЖНЯЙТЕСЬ EHlEsGOTO 18

148 PRINTOTflHHHO.BCE РЕШЕНО ВЕРНОs&OTO 18

158 PRINTХОРОШО.ОДНА ОШИБКА:GOTO 18

168 PRINTПОСРЕДСТВЕННО.ДОПУЩЕНЫ N ОШИБКИ:GOTO 18

178 ENII

Отметим основные области применения метода Моите-Карло: решение нелинейных уравнений, вычисление экстремумов (в том числе глобальных у многоэкстремальных функций многих переменных), вычисление определенных интегралов большой кратности и др.

§ 5.5. Корреляционный анализ

Корреляция является признаком, указывающим на взаимосвязь ряда численных последовательностей. П.арная корреляция характеризует взаимосвязь двух последовательностей Xi и I .

Коэффициент парной корреляции R =

W . N N

I т-( I Xi I уЛ/N ,=1 \/= ,=1 /

(5.23)

характеризует степень отклонения связи между Xi и у, от линейной. Если \R\ близок к 1, то эта связь линейна, т. е. yi=axi+b.

причем знак R определяет знак коэффициента а. Если R> О, то а> О, и напротив, при /?<0 а<0.

Программа 5.16.

описывающей связь между некоторым числом N пар значений Xi и yi, обеспечивая , при этом наименьшую среднеквадратичную погрешность. Графически эту задачу можно

65 РР1НТВЫЧИСЯЕНИЕ КОЭФФИЦИЕНТА ПАРНОЙ КОРРЕЛЯЦИИ

10 IWUTВВЕДИТЕ Н=Н

20 LETA=0!LETB=0!LETC=0!LETri=0!LETE=0

30 РРШТВВЕДИТЕ ПОПАРНО X<I),V<I)

40 FOR 1=1 TO H!PRINT!3.0!I=I

45 INPUTX<I>=X!INPUTV<I>=V

50 LETA=A*X5LETB=B+V!LETC=C+X

60 LETIi=Ii+V2!LETE=E+X*V:HEXT I

70 LETR= <E-АжВ/Н > /SQR < < C- СA"2 ) /"N >ж < B- <B"2 > /N > )

80 РК1НТ!Р1.9!К0ЭФ.КОРРЕЛЯЦИИ R=R

Пример. Для N=5 и yi(xi}, равных 2(0,95); 4,05(2,1); 5,8(3); 8.1(4,1) и 9,2(4,9), получим /?=0.9987280191.

Порядковая корреляция по Спирмену оценивается коэффициентом порядковой корреляции [18]

представить следующим образом - в облаке точек Xiyi плоскости ху (рис. 5.4) требуется провести прямую так, чтобы величина всех отклонений отвечала условию

где у {xi) - зависимость (5.24). Для этого

где Ak и Bk - место (ранг), которое занимают Xk и yk при убывании Xk. Программа 5.17.

18 PRINTВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТА РАНГОВОЙ КОРРЕЛЯЦИИ

28 ШРиТВВЕДИТЕ N=N:LETS=0

30 FOR 1=1 ТО NSPRINT!4.0!ДЛЯ 1=I

48 ШРИТВВЕДИТЕ Aj-B А,В

58 LETS=S+<A-B)"2!NEXT I

68 LETR=1-6*S/N/<N"2-1>

78 PRINTIFI.S!КОЭФФИЦИЕНТ R KOP=R!ENIi

Пример. Для N=7 и А (В), равных 5(6), 4(7), 3(3), 7(5), 2(1), 1(2), 6(4), получим /?„ = 0,6428571429.

Вычисление коэффициента корреляции на специализированных ПЭВМ выполняется микропрограммно. Так, на ПЭВМ FX-702P для этого выполняются следующие операции.

1. Нажатием клавиш Fi и SAC обнуляются ячейки памяти статистических расчетов.

2. По схеме

вводятся пары чисел xi и {/,-. Ошибочно введенная и обработанная пара исключается нажатием клавиш Fi и DEL/STAT.

3. Вводом команды COR вычисляется R.

§ 5.6. Регрессионный анализ (приближение функций по методу

наименьших квадратов)

Линейный парный регрессионный анализ заключается в определении параметров эмпирической линейной зависимости

нужно приравнять нулю частные производные

dU дЬ,

J у-

-=2 [г/.-(6о+6а-,)].

= [«/.- (йо-f *!>:,) Xi],

i = l

что дает для определения неизвестных коэффициентов Ьй и fci систему линейных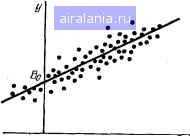

у (х) ==b,x+bo.

(5.24)

Рис. 5.4. К линейной регрессии

\ = l 1 = 1

Программа 5.18.

05 PRINTЯИНЕйНйЯ РЕГРЕССИЯ

10 INPUT ВВЕДИТЕ N=N

20 LETft=0!LETB=0sLETC=0:LETIi=0

38 PRINT!3,0!ВВЕДИТЕ Х<П»7<1>

48 FOR 1=1 TO H:PRINT 1=I

58 INPUT X<n=Xs IHPUT V4n=V

60 LETft=ft+X!LETB=B+Vs LETC=C+X"2

70 letri=il+X*V!next I

80 LETBl=<fti«B-N*D><ft--2-N!«C)

90 LETB8=«:B-Bli«ftVN

188 PRINT!F1.9!V=B8+B1!«X

lie INPUTbbeahte X=X

128 РК1НТ7<Х>=В8+В1жХ!Б0Т0 118!ehb

Пример. Пусть имеется совокупность из /V = 5 пар y,{Xi): 5,5(2); 6,3(4); 7,2(6); 8(8); 8,6(10). Введя эти данные, получим 6о=4,75 и 61=0,395. Следовательно, зависимость у (х) имеет вид

Программа предусматривает вычисление у по заданному значению х.

При необходимости программа может быть легко дополнена вычислением коэффициента парной корреляции R (5.23) или среднеквадратичной погрешности

6о Xiy,

у (а-) = 4,75-f0,395а:.

что позволит количественно оценивать степень приближения точек ад к прямой (5.24).

Линейная регрессия с помощью специализированных ПЭВМ выполняется микропрограммно. Так, у ПЭВМ FX-702P предусмотрены операторы LRA и LRB для вычисления параметров А==Ьо и B = bi линейной регрессии у (х)=А-\-Вх, а также операторы EOY для вычисления у по заданному X и ЕОХ для вычисления х по заданному у. Одновременно при этом вычисляется коэффициент корреляции R и другие статистические параметры массивов а, и у,-, описанные ранее (всего 17 параметров).

Последовательность вычислений рассмотрим иа примере к программе 5.18 (см. ниже).

Как показывает данный пример, ПЭВМ FX-702P, специализированные иа научно-технические и статистические расчеты, обеспечивают микропрограммное (т. е. без ввода внешних программ) вычисление важнейших характеристик двумерных массивов xiyi, а также проведение корреляционного и линейного регрессионного анализа. Указанные выше операторы могут использоваться и в составе внешних программ, что резко упрощает последние.

Нелинейная парная регрессия сводится к получению заданной нелинейной зависимости у (а) (нелинейной по независимой переменной а, но линейной по параметрам этой зависимости!), приближающей совокупность

Вычисление суммы а,-Вычисление суммы у. Вычисление суммы xf Вычисление суммы yf Вычисление суммы x,i/,-Вычисление а Вычисление у Вычисление у при х=5 Вычисление х при i/=6,725

MY EOY 5 ЕОХ 6.725

SX=30 SY=35.6 SX2=220 SY2 = 259.74 SXY = 229.4 EXE 6

EXE 7.12

EXE 6.725

EXE 5

boN + bi X X №.

N N N

60 Xi+b, Y. xi==T "•У-1=1 /=1 1=1

Решение этой системы:

N N N

Z I №-Л I A-ii/i 6,=