

|
|
Главная -> Справочник по алгоритмам 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 [50] 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 § 6.9. Функции Струве, Ангера и Вебера Функции Струве Ну, (х) входят в общее решение ш=aJ„ {х) +bY„ [х) + Н„ {х} дифференциального уравнения второго порядка вида x-+x-+{x-v) ш=-~ т/яГ (v-f 1/2) Функции я» (х) вычисляются разложением в ряд [42]: НЛх) r(v-f3/2)L 3.(2v + 3) 35-(2v + 3).(2v-f5) Модифицированные функции Струве L« (х) = z=-je~H„(}x) можно разложить в ряд вида (Х/2Г r(v+3/2)L 3.(2v + 3) 3-5-{2v + 3)-(2v + 5) + ... Таким образом, разложения в ряд Я, (х) и Lv (х) различаются лишь тем, что члены в квадратных скобках у ряда Я» (х) знакочередующиеся, а у ряда £v (х) - с одним Программа 6.19. знаком. В программу для вычисления этих функций нужно включать фрагмент, вычисляющий r(v--l,5), например, по аппроксимации гамма-функции полиномом. Программа 6.19. Пример. Погрешность £ = 1 • 10"", Я, (5) =0,8078118816. Яо (0,5) = 0,30955589, Я 8 (4) = -8,249323233, £, (0,5) = = 0,05394217833 и L-e (6) =3,327822061. Функции Струве могут вычисляться также с (юмощью численного интегрирования с применением интегральных представлений (Rev> -1/2): Н, [х): 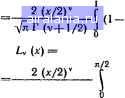 т/я Г (V+1/2) tV~sm {xt) dt. sh (xcosO) sinOrfe. Однако и в этом случае необходимо вычисление гамма-функции Г (v--l/2). Функций Ангера /v {х) имеют интегральное представление вида /. W =~ COS (vO-xsin 0) do. При целом v-n Jv(x)-Jn(x). В общем 10 PR I NTВЫЧИСЛЕНИЕ ФУНКЦИЙ СТРУВЕ ШОО И UKXi 15 ШРиТВВЕДИТЕ 8 ДЛЯ тСУ:> И 1 ДЛЯ LUCX) К 28 INPUTBBEAHTE UjX =UfVeLETA=V*V:IF K=0 THEN LETA=-A 30 LETX=U+1.5!LETH=15 LETI=1з LETJ=1 48 LETB=ABS(:X)!LETIi=l 58 IF B<1 THEN 70 68 LETri=Ii*BsLETB=B-ls&OTn 58 78 LETF= СC.835868343*6-. 193527S18)!«B+.4S2199394):*.B 80 LETF=(:<<F-.7567е4078)жБ+.918286857)-«B-.S97e56937}*B 90 LETF= С СF+.988285891)»3-,577191652)*B+1 188 LET&=F*Ii.X5 IF X<e THEN LET&=SPI.SIN<»PI:*.X).D..F 118 LETI=I+2:LETH=H*A>I.<2!tsU+n5LETW=..i 128 LETJ=J+H!IF ABS<.J-W>>=lE~ie THEN 118 130 LETU!=<<VV2)-<U+l>)!ts2a!j,G-SQR«:#PI> 148 IF K=l THEN 168 158 PRINTHUf.X:)=Ws&nTn 20 160 PRINTLU<X>=WsGnTO 28SEND le PR I NTВЫЧИСЛЕНИЕ ПОПНЫК ЭЛЛИПТИЧЕСКИХ ИНТЕГРАЛОВ KOD И Е<:и> 15 PRINT С ПРИМЕНЕНИЕМ АППРОКСИМАЦИИ 20 INPLITВВЕДИТЕ М<=1 h=M:LETM=l-M 30 LETK= < <. 01451196212*M+. в374£563?13):*.И+. 03596092383>.*И 35 1 ЕТК= < К+. 09666344259:> жМ+1.38629436112 40 LETW= <.80441787812*H+.83328355346)жИ 45 LETW=< 86888248576)ЖМ+. 12498593597).*И+. 5 58 LETK=K+W*L06a1>!pRIHTK<M>=K 68 LETE= С. 81736586451жИ+, 84757383546 ) :«М 65 LETE=<<E+.e626e6eig2J*M+.44325141463).*t«)+l , 78 LETW=<.8е52644Э639:«М+.84869697526)*И 75 LETW=<aiJ+.e928ei80e37).*H+,2499836831>*M 88 ЬЕТЕ=Е+и1ж1 Пб а ): PR I ИТ Е < И )= Е: 6010 28: ЕНП случае функции Ангера удобно вычислять с помощью численного интегрирования. Так, для v=l, Л=0, В = л,. x=0,5, М = 4 получим /, (0,5) =0,5844468394 при сЛгЮ с. Аналогичным образом несложно организовать вычисления функций Вебера £v (х) =-\ sin (vO-x sin 8) я J §6.10. Гипергеометрические функции Гипергеометрнческие функции F (а, Ь, с, х) являются частным решением дифференциального уравнения х(!-х)-+[с-(а+6 + 1)х] - aufo = 0. Они могут вычисляться с применением следующего ряда: f (а, 6, с, х)~1 + / = 0 у = (g-f/) (fc-f/) (l+y) (с+/) J++" гае Л/ = 22, едг.) -поправка. Значения U<1, сФО. -1, -2,... При 0<(а, 6)<с и -0,1x0,8 погрешность 6<:5-10~*, но обычно существенно ниже. Программа 6.20. и (а, 6, X) = £ (а, 6, х) sin л6 ( Г (1-fa-f 6)-Г (Ь) „,-ь F {\+a-rb,2-b, X) Г (а)-Г (2-й) Вырожденная гипергеометрнческая функция F (а, Ь, х) вычисляется разложением в ряд f fr («+/) , = 1 у=о дающем при Л=22 погрешность б<1-10" для 0<с<6 и -5<x<!0. Программа 6.21. Пример. F {I; 1; 0,5) = 1,648721721 при точном значении 1,648721271. С помощью гипергеометрнческих функций можно найти большинство элементазных и специальных функций [36, 42]. Например, функция F(a,a\x) при 6=а дает значение е". Так, в приведенном примере при 6 = 0,1 и х = 0,5 получаем £ (1; I; 0,5) =6"-=. = 1,648721271. Аналогичный результат дает вычисление f (3; 3; 0,5) при а = й = 3. §6.11. Дилогарифм Дилогарифм - интегральная !п/ функция dt, может вычисляться с 10 PRINTВЫЧИСЛЕНИЕ ГИПЕРГЕОМЕТРНЧЕСКОй ФУНКЦИИ F<AfBrC/K> 20 INPUTВВЕДИТЕ ftrB,Cft/BrC 30 INPUTВВЕДИТЕ J<=X:LETF=L6T<23J 40 FOR 1=23 TO 1 STEP -l!LETD=I-l 58 LETF=F*<B+A>*<Ii+B>-<Ii+C>/I*X+l 60 NEXT l!PRINTF«:A,B,CfX)=F!80T0 30: END Пример, f (1;. 1; 2; 0,5) = 1,386294358 при точном значении F (\; 1; 2; л) = =-х- In (1-A) = 1,38629436! и /с~8 с. Первым независимым решением уравне- Куммера -+(6-х) dbi 1й - сы = 0 является вырож.аенная гипергеометрическая функция F {а, Ь, х) =М {а, Ь, х). Через нее и гамма-функцию может быть найцено второе Программа 6.21. помощью численного интегрирования методом Гаусса (программа 4.42). Задав А=1, В=х и М = 8 для А = 0,4, получим / (х) = = 0,7275863075 при точном значении 0,727586308 и 10 с. Дилогарифм тиожет вычисляться и по разложению в ряд: n-) = J (-1)-, 0<х<2. 10 PRINTВЫЧИСЛЕНИЕ ЕЫРОШДЕННОй ГИПЕРГЕОМЕТРИЧЕСКОЙ 15 PRINT ФУНКЦИИ F<ft*B*X) 20 INPUTВВЕДИТЕ А,ВА,В 30 INPUTВВЕДИТЕ X=X!LETF=L6T<23) 40 FOR 1=23 ТО 1 STEP -l!LETIi=I-l 50 LETF=F5<i<Ii+A)!«X/<D+B)/I+l 60 NEXT I:PRINTЗНАЧЕНИЕ F<A*B,X>=F 70 60T0 301END Программа 6.22. 05 PRIHT •ВЫЧИСЛЕНИЕ ДИ ЛОГАРИФМА 10 INPUT-ВВЕДИТЕ Х=Х: LETV=X-1 . £0 LETI=0: LETS=0: LETR=l! LETP=1 30 LET 1=1-H! LETR=-R: LETP=P:«V 40 LETIi=Ri«P."I"2: LETS=S-Hi 50 IF ABSai)>lE-9 THEN 30 60 PRINTДИЛОГАРИФМ F<X)=S ?0 SOTO 10: END Пример. Для x-0,\ получим / (x) = = !,299715. §6.12. Функции Кельвина функции Кельвина относятся к классу функций Бесселя и являются решениями дифференциального уравнения записываемыми в виде о) = ЬеГу {x)+jbeu {х). Функции Кельвина вычисляются разложением их в следующие ряды [36]: berv {х) = с» COS [(3v/4-f*/2)Kl /jc2 4* k\r {v + k+l ) u;• beiv {x) • /xy у sin [(3v/4-f fe/2) я] /XY \2/ Д feir (v+ft-f 1) V 4 j " * = 0 Для практики интерес представляют в основном функции Кельвина целого порядка v - n (и = 0, 1, 2, ...), в частности функции Ьегх и beix (лг = 0). При целом v = n имеем Г (v+k+\) = {n+k}\, что упрощает вычисления, поскольку отпадает необходимость определять гамма-функцию r(v--fe-hl) для каждого члена ряда. Программа 6.23. Пример. При заданной погрешности £=1.10-* получим ЬеГ2 (1,55) =0,059944 и beis (1,55) = -0,259803 (все цифры верные). § 6.13. функции Дебая и Зиверта Интегральная функция Дебая D„ {х) = Г t"dt легко находится численным интегрированием с помощью программы 4.42. Так, дляу4=0, В=>:=1 нп = Ы=1 приуИ=4 получим D, (х) =0,7775046341 при точном значении 0,777505, аналогично Dt{l) = = 0,6137185176 (время счета менее 10 с). Интеграл Зиверта Ziv (z) =\ е"""" dx также легко находится численным интегрированием. Для 2=1, Л=0, В = е = я/2 и M = 8 получим Ziv (1) =0,3282894817 при точном значении 0,328286 и 16 с. §6.14. Интеграл вероятности и родственные ему функции 2 Г 2 Интеграл вероятности eri х~-\ е~ dt желательно вычислять с высокой точностью. Это возможно с применением разложения erf X в ряд [36]: ,,f, 2 f (-1)""- L п\ (2n-f I) Дополнительный интеграл вероятности erfc х=-г- \ е- dt=\ -eri х. л/л J 10 PRINTВЫЧИСЛЕНИЕ ФУНКЦИЙ КЕЛЬВИНА BERCXj BEICX) 20 ШРиТВВЕДИТЕ В ДЛЯ ВЫЧИСЛЕНИЕ BERCX) И 1 ДЛЯ ВЕКХ) ?С 30 INPUTЗАДАЙТЕ ПОГРЕШНОСТЬ Е=Е 40 ТЬРиТЗАДАйТЕ КЬУ. UjX:LETA=<X./2)ai:LETB=X*X.4:LETI=0:LETP=l 45 LETI=I-H:LETP=P*I:IF KU THEN 45 50 LETR=l.P!LETe=v3»sU>4)*#PI:lF C=0 THEH 60 55 LETZ=SIN(:o>:GOTn 70 60 LETZ=COS<G> 70 LETS=R*Z:LETK=0 80 LETK=K+1: LETR=R*B.K>«:K-fU>: LETG=«:3stiU,4+K2>3*#PI 82 IF G<2*#PI THEN 90 85 LETGj=Q-2*#PI:&0T0 82 " • 90 IF C=e THEN 110 108 LET2=SIN<Q>:60T0 128 110 LETZ=COS<Q) . • • 120 LETl.J=S:LETS=S+R*Z 125 IF ABSC2XE THEN 80 • • 130 IF ABS<S-W)>=E THEN 88 148 LETS=S!tsA:IF C=l THEN 168 158 PRINTBERU<>i>=S:C-.OTO 48 160 PRINTBEIU<X)=S:C-.OTn 40:ЕНБ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 [50] 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 0.0447 |