ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ

1 2 5 7 19 26 1 1 3 4 11 15

Колышки под прямой расположены в точках (1, 1), (3, 5), (И, 19), а колышки над прямой - в точках (1, 2), (4, 7), (15, 26),...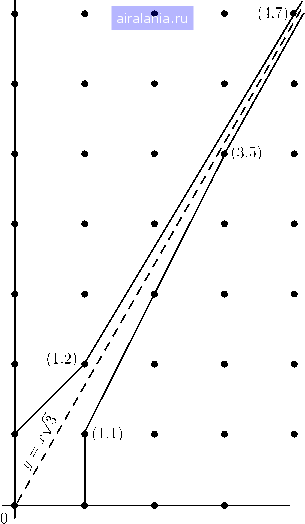

Рис. 3

Большинство элементарных теорем о непрерывных дробях имеют простую геометрическую интерпретацию. Обозначим через Рп точку (Л, Вп). Рекуррентные соотношения (8) и (9) по-

казывают, что вектор от Рп-2 до Рп {Рп-2 Рп - две последовательные вершины одной из ломаных) равен целому кратному вектора от начала О до Pn-i- Соотношение (10) можно интерпретировать как утверждение о том, что плош;адь треугольника Рп-гРп при любом п равна . Это утверждение можно вывести непосредственно из описанной выше конструкции с веревкой: в самом деле, очевидно, что в треугольнике OPn-iPn нет ни одной целой точки, помимо вершин; кроме того, можно легко доказать, что плош;адь любого треугольника, обладаюш;его этим свойством, равна .

Замечания к главе IV. Лучшее из имеюш;ихся па английском языке изложений теории непрерывных дробей содержится в книге Христаля (см. Chrystal, Algebra, vol. П, chs. 32-34). Па русском языке эта теория излагается в книге А. Я. Хинчина «Цепные дроби», Физматгиз, 1961*). Типичной работой по этому предмету является работа Перрона (Perron, Die Lehre von den Kettenbriichen, Teubner, 1929). Доказательства различных результатов, приведенных в этой главе без доказательств, можно найти у Христаля или Перрона. О диофантовых приближениях читатель может справиться в книгах Перрона, Пивена или Касселса (см. Perron, Irrationalzahlen, Goschens Lehrbucherei, vol. I, 1947; Niven, Irrational Numbers, Carus Math. Monographs, № 11, 1956; Cassels, Introduction to Diophantine Approximation (Cambridge Math. Tracts, № 45, 1957)) и в книге Хинчина*).

п. 1-6. Практически вся эта теория принадлежит Эйлеру.

п. 7. См. (9, ch. И); Perron, § 8 или А. Я. Хинчин, гл. II*).

п. 8. Ссылки на таблицы можно найти у Перрона, стр. 100 или в (, vol. II, ch. 12). Об удобных методах вычисления непрерывных дробей для квадратичных иррациональностей, см (, р. 372).

п. 10. Вывод непрерывной дроби для е и пр. см. у Перрона (Perron, §§ 31 и 64) или в заметке Дэвиса (С. S. Davis, J. London Math. Soc, 20 (1945), 194-198).

п. 11. Относительно задачи о скоте см. Thomas Heath, Diophantus of Alexandria (Cambridge, 1910), pp. 121-124 и ( vol. II, pp. 342-345).

П. 12. Cm. F. Klein, Ausgewahlte Kapitel der Zahlentheorie (Teubner, 1907), pp. 17-25. Идея, кажется, принадлежит Смиту (см. П. J. S. Smith, Collected Math. Papers, vol. 2, pp. 146-147).

*) Ссылки на книгу A. Я. Хинчина добавлены мной. {Прим. перев.)

ГЛАВА V

СУММЫ КВАДРАТОВ

1. Числа, представимые в виде суммы двух квадратов. Вопрос о представимости чисел в виде суммы двух квадратов - очень старый вопрос; он рассматривается еще в «Арифметике» Диофанта (около 250 года нашей эры), но точный смысл утверждений Диофанта неясен. Правильный ответ на этот вопрос впервые дали немецкий математик Жирар (Albert Girard) в 1625 году и немного позднее Ферма. Возможно, что у Ферма имелось доказательство его результата, но первым из известных нам доказательств является доказательство Эйлера, опубликованное в 1749 году.

Легко установить, что некоторые числа не представимы в виде суммы двух квадратов. Во-первых, квадрат любого четного числа сравним с О по mod 4, а квадрат любого нечетного числа сравним с 1 по mod 4. Отсюда следует, что сумма любых двух квадратов сравнима с О + О, или с О + 1, или с 1 + 1 по mod 4, т. е. с О, 1 или 2 по mod 4. Таким образом, ни одно число вида 4А; + 3 не представимо суммой двух квадратов.

Но мы можем пойти дальше. Пусть число N имеет простой множитель q вида 4А; + 3; уравнение + = N влечет сравнение х = -у (mod TV), а так как -1 является квадратичным невычетом по модулю д, это сравнение разрешимо лишь при X = {) (mod g) и 2/ = О (mod q). Значит, х и у делятся на д, следовательно, TV делится на q и уравнение х -\- у = N можно сократить на q. Если TV = qNi и TVi еще делится на д, то такое же рассуждение показывает, что TVi делится на q и так далее; таким образом мы находим, что точная степень д, делящая TV, должна быть четной. Итак, всякое число, представимое в виде суммы двух квадратов, содержит в своем разложении лишь четные степени простых вида Ак + 3. Прежнее условие состо-