Рассмотрим условия пренебрежения обратной связью по ЭДС двигателя и характер ее влияния в системе с упругой связью. Передаточная функция разомкнутого токового контура в соответствии с рис. 2.4, б может быть представлена в виде

Wp2 (Р) - W;. ip) W, ip) - W;. (p) ...... . , (2.27)

Wo.c{p) =

ту + 2I2T2P + 1

т,иР\Т..,Р-\-1){ту-21,т,р1]

Поскольку параметры передаточной функции Wo. с (р) зависят от многих первичных параметров электропривода, то анализ влияния обратной связи по ЭДС двигателя удобно вести по обобщенным параметрам соу, q, Тэм. я. ii- При этом целесообразно рассмотреть следующие характерные случаи сочетания параметров СЭП:

1. Пм » д = 0,01-0,1; Т, = (5-10) Т22; озу -= (0,5-г-1)-; lj = 0,05-4-0,15, что в среднем действительно

Tz-2

для секционных приводов бумагоделательных машин.

2. Тзм » Тг\ q = 0,01ч-0,1; = (5-10) Тг; сОу -= (0,5-1)---; 1 = О, что является идеализированным случаем

для электроприводов бумагоделательных машин и других агрегатов, когда отсутствует демпфирование механизма.

3. Тз„ 10 ЯоГз; = 0,1-4-0,5; T« = (1-3) Тг; ---= (2-4)--; li?0, что чаще всего действительно для электро-

приводов агрегатов небольшой мощности, и в частности металлорежущих станков [19].

Поставленную задачу удобно решать с помощью метода логарифмических частотных характеристик, позволяющего получить известную общность результатов исследований. На рис. 2.5 представлены ЛАХ для рассмотренных случаев сочетания параметров электропривода. Как видно из представленных характеристик, в первом случае ЛАХ Wo. с (to), показанная на рис. 2.5 сплошной линией, лежит вне зоны существенных частот токового контура, обозначенной прямоугольником. Следовательно, ЛАХ (о)) в зоне существенных частот токового контура будет равна нулю и характеристика Up2 (оо) останется без изменения. Это говорит о том, что влияние обратной связи по ЭДС двигателя в данном случае практически отсутствует и расчет переходных процессов в системе может быть выполнен без учета этой связи.

Частотные характеристики для второго случая сочетания параметров привода представлены на рис. 2.5 штриховыми линиями. При этом ЛАХ Wo. сМ располагается в зоне существенных частот токового контура. Характеристика (со) в данном случае отлична от нуля и" результирующая ЛАХ разомкнутого контура

тока (со) намного отличается в зоне существенных частот от характеристики Wp2 (со). Однако в зоне низких частот характеристики Wp2 (со) и (со) практически совпадают. Это позволяет сделать вывод, что переходный процесс в токовом контуре в действительности существенно отличается от процесса, полученного без учета обратной связи по ЭДС двигателя, но конечное значение тока якоря при предельном токоограничении в том и другом случае практически совпадает. Как видно из представленных на рис. 2.5 переходных характеристик тока якоря i,j (г/Тг)» влияние обратной связи по ЭДС двигателя приводит к увеличению длительности и колебательности переходных процессов в токовом контуре; при настройке токового контура на ОМ перерегулирование тока якоря составляет около 30%, а время переходного процесса возрастает в 4-5 раз.

Обратимся к рассмотрению третьего случая сочетания параметров СЭП. Соответствующие частотные характеристики представлены на рис. 2.5 штрихпунктирными линиями. Резонансные всплески характеристики Wq. {о)) лежат вне зоны существенных частот токового контура, что говорит об отсутствии влияния обратной связи по ЭДС двигателя в начальной части переходного процесса. Однако в низкочастотной области характеристика Ws (со)

уже при Тэм 10 /2oTv2 обусловливает появление статизма токового контура. Следовательно, в рассматриваемом случае влияние обратной связи по ЭДС двигателя эквивалентно ее влиянию в жесткой системе, а выражение Тэм>10 «цТз может служить условием пренебрежения этой связью при анализе переходных процессов в системах подчиненного регулирования.

Настройка динамики электроприводоЬ без применения специальных корректирующих устройств. Рассмотрим коррекцию систем подчиненного регулирования электроприводов с упругими передачами путем перестройки регуляторов и рационального выбора быстродействия контуров скорости и тока. Для получения в СЭП качественных переходных процессов производится соответствующая настройка как токового, так и скоростного контуров. Коррек-

3 Заказ № 24 65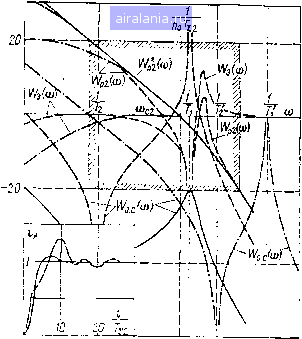

Рис. 2.5. Логарифмитеские частотные и переходные характеристики токового контура

цию системы начинают обычно с внутреннего - токового - контура. При этом параметры ПИ-регулятора тока выбираются в соответствии с условиями;

2 Т,-

(2.28)

Чаще всего принимают /?о 2, что обеспечивает настройку контура на ОМ; иногда, например в ЭП бумагоделательного производства, принимают riQ = \ [6 ], что обеспечивает большее быстродействие контура тока, но и увеличивает его колебательность.

Общая передаточная функция разомкнутой СЭП может быть получена с помощью правила Мэзона (см. § 1.3) непосредственно по структурной схеме (рис. 2.4, а). Согласно этому правилу, передаточная функция разомкнутой СЭП будет

(2.29)

WiWiy ITiiWiii -4- WuWiv

где IFjip - передаточная функция прямого пути от Ug. до ид.,;

- передаточная функция данного контура.

После подстановки соответствующих значений параметров и ряда преобразований искомая передаточная функция может быть представлена в виде

(Р) - Г„ , (р) -.(1д..Р- 1)(ТмГер- \ Г.Р-М)

1 kfipTj:, {njp ~ 1) (ГмГсР + Тдр 1) 1-1

MS (Т,Р -f 1) + «0722+0 (яТту-Тр + Г)

(2.30)

Второй сомножитель данного выражения характеризует влияние обратной связи по ЭДС двигателя на динамику контура скорости. В первом сомножителе выражение

-- - 32 (Р) (2.31)

Представляет собой передаточную функцию замкнутого контура тока без учета действия ЭДС двигателя. В передаточной функции (2.30) учтены все параметры СЭП в общем случае их сочетания. Это выражение удобно для анализа и синтеза системы частотными методами и дает возможность исследовать влияние отдельных параметров на динамику СЭП.

Влияние и способы оптимизации токового контура. Значение 72 = Тг. п + Тд. я в общем случае определяется степенью подавления пульсаций тока якоря и выбором желаемого соотно-

шения между быстродействием токового и скоростного контуров. Теоретически значение Та может находиться в пределах О < Т22< Гя.

Исследование динамики системы с помощью логарифмических частотных характеристик, построенных по выражению (2.30), показывает, что увеличение Тг до значения Т приводит к несущественному подавлению резонансного пика ЛАХ объекта при (Oi » (Иу (при малых значениях Hi). При T22>Ti токовый контур начинает весьма эффективно снижать пик ЛАХ.

Следовательно, для подавления упругих колебаний в системе можно увеличить инерционность токового контура, обеспечивая

--<;«у при сохранении его типовой настройки на ОМ. Дан-

ное решение дает более эффективное подавление пика на частоте Ыу (в д/по TatUy раз), чем перестройка регулятора тока, рекомендованная в работе [13]. Однако такое решение оказывается целесообразным лишь при достаточно высоких значениях соу, когда Tl < 0,1 Тд. При Tl » Тя снижение быстродействия токового контура нецелесообразно из-за ухудшения отработки возмущений в виде изменения напряжения питающей сети и увеличения влияния изменения параметров контура тока на динамику контура скорости [59]. Поэтому рациональным в рассматриваемых системах является выбор Tv2 » (0,05-г-0,2) Тд и сохранение типовых настроек токового контура.

Коррекция контура скорости. Задачей коррекции контура скорости является получение его наибольшего быстродействия при удовлетворительном подавлении упругих колебаний в СЭП. Из передаточной функции разомкнутой системы (2.30) видно, что условия подавления упругих колебаний определяются как настройкой регулятора скорости (PC), так и сочетанием параметров привода, в частности соотношением частот сОу и l/Ti, где Tvi - суммарная малая постоянная времени контура скорости. В качестве PC может быть применен пропорциональный (П) или пропорционально-интегральный (ПИ) регулятор, что определяется соотношением параметров объекта и требованиями к статике и динамике системы. В первом случае передаточная функция PC будет

р.с(р)=р.с, (2.32)

по втором случае

W-p.c(p)-Pi " (2.33)

Tj.p

При 1/Т21>соу условие несущественности влияния упругости первого рода, полученное с помощью исследования выражения (2.30) частотным методом, может быть записано через частоту среза контура скорости в виде

о)с1 < 1ту. (2.34)

при этом в большинстве случаев имеет место весьма низкое значение coi, в особенностипри малых q, что не удовлетворяет требованиям, предъявляемым к быстродействию СЭП промышленных агрегатов.

Более благоприятным случаем является l/T2i<o)y, когда инерционность СЭП способствует подавлению резонансного пика ЛАХ объекта на частоте сОу. В этом случае условие. несущественности влияния упругости первого рода будет

«С.1 < lltoyTvi,

что обеспечивается следующими параметрами PC:

-г.с = р1 = rTMSiWyTsi;

(2.35)

(2.36)

При 1/72 1<о)у значение со может быть увеличено в cOyTi раз по сравнению с предыдущим случаем. Вместе с тем в рассматриваемом случае возникает задача отыскания оптимального значения Гь когда достигается надежное подавление упругих колебаний при оптимальном протекании переходных процессов в системе. При настройке контура скорости с П-регулятором на ОМ или с ПИ-регулятором на СО, что определяется требованиями к качеству динамики системы, значение может быть определено по формуле

СО.-СОу.

(2.37)

где Ло -запас по амплитуде ЛАХ W разомкнутой системы на частоте сОу.

Для удовлетворительного подавления упругих колебаний достаточно иметь Л о = 2][U ]. Поскольку при стандартных настройках coci = I/(2T2i), то из выражения (2.37) можно найти требуемое значение Ть равное

721- L -• (2.38)

Л/2Ы toy

Значение Тг определяется суммарной инерционностью контура скорости:

721 = 7д.с +«022+ (2.39)

где т\ - инерционность фильтра, включенного на выходе PC. Зна-

чение tj целесообразно выбрать по формуле z\ = [q требуемое значение Гд.с будет

Тд.с -

тогда

(2.40)

il? СОу

С учетом найденного значения Ti формулы настройки PC (2.36) примут вид

(2.41)

Jy V liQ

При этом частота среза контура скорости будет

(2.42)

СОу - 40-80

5 с-1

Для промышленных агрегатов с = 0,03 - 0,1; q = 0,01-0,1 частота со будет 0,5-

Оптимизация динамики СЭП с применением специальных корректирующих устройств. Полученное изложенными выше способами быстродействие СЭП не всегда оказывается достаточным, и для улучшения динамических характеристик системы необходимо применять специальные корректирующие звенья, предназначенные для подавления упругих колебаний. Рассмотрим системы ЭП, у которых 7", д<7„, что является более сложным случаем влияния упругой связи на динамику СЭП. Коррекция СЭП с Тм.д>Тм рассмотрена, в частности, в работе [13].

В соответствии с изложенным выше токовый контур должен иметь максимальное быстродействие и настраиваться на ОМ. Параметры регулятора тока якоря выбираются по формулам (2.28), что позволяет в большинстве случаев иметь частоту среза контура тока С0с2 = 50 - 100 с". При этом передаточная функция замкну-тоготокового контура определяется выражением (2.31).

Оптимальные динамические характеристики контура скорости определяются совместным выбором параметров PC и вводимого корректирующего звена (КЗ). При этом необходимо оптимизировать электромеханическую связь [29], т. е, добиться наибольшего быстродействия СЭП при оптимальном подавлении упругих колебаний. Проведем синтез параметров PC и КЗ частотным методом.

На рис. 2.6 представлены нормированные логарифмические частотные характеристики системы, построенные для наиболее характерного сочетания параметров СЭП. ЛАХ Wqi объекта регулирования контура"скорости (без PC) построена по выражению (2.30). Она имеет характерные пик и провал на частотах сОу = (-y/qTTf.)

и соз = (л/7\Д7)" Для увеличения быстродействия СЭП необходимо в первую очередь подавить резонансный пик на частоте соу. Следует заметить, что компенсация провала ЛАХ нецелесообразна ввиду ослабления электромеханической связи и возможности появления незатухающих колебаний механизма на частоте со д.

Последовательная коррекция СЭП. В данном случае корректирующее звенодолжно быть фильтром с ограниченной полосой про-