пускания. Основными требованиями к такому фильтру являются: подавление частот механического резонанса, плавное и независимое изменение частоты настройки и добротности фильтра, высокая стабильность работы.

В принципе этим требованиям могут удовлетворять как пассивные, так и активные корректирующие звенья. Однако использование пассивных /LC-фильтров практически затруднительно ввиду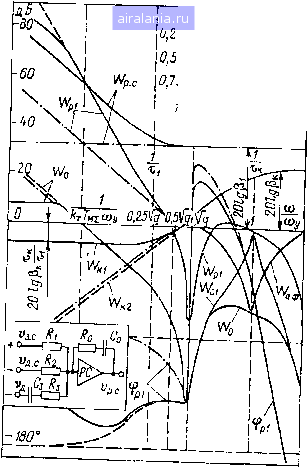

Рис. 2.6. Логарифмические частот]]ые характеристики СЭП с упругой связью первого рода

весьма низких частот упругих колебаний, составляющих обычно единицы герц. Поэтому более целесообразным является применение активных фильтров, выполненных на базе операционных усилителей или эмиттер ных повторителей [33]. Активный полосно-заграждающий (ре-жекторный) фильтр с использованием перестраиваемого двойного Т-образного ЯС-моста и эмиттерного повторителя [59] вводится на выход PC и имеет частотную характеристику %а.ф, инверсную по отношению к резонансному пику ЛАХ объекта (рис. 2,6). После этого ЛАХ объекта не содержит пика на частоте соу, что дает возможность существенно повысить быстродействие СЭП. Попутно активный фильтр формирует частотные характеристики объекта, необходимые для настройки контура скорости на ОМ или СО. При этом постоянная времени фильтра датчика ско-

йремени фильтра датчика ско рости (ДС) может быть выбрана исходя из подавления высокочастотных пульсаций и составляет в среднем Гд, с = 0,01-4-0,03 с.

PC может быть в общем случае пропорциональным или пропорционально-интегральным и иметь соответственно передаточные функции (2.32) или (2.33). Параметры PC выбираются по условиям:

р.с р1 = 0,57л1ц tOy;

q (Оу

(2.43)

Частотные характеристики PC Тйр. с и скорректированной системы ttpi, Фр1 показаны на рис. 2.6, откуда видно, что при пропорциональном PC система имеет настройку на ОМ, а при пропорционально-интегральном PC - на СО при частоте среза =

= 0,5д/<7 соу.Для промышленных агрегатов coi в среднем составляет 2-10 с~. Соответствующие нормированные переходные характеристики скорости двигателя д и механизма v„ при управляющем Ug. с и возмущающем воздействиях представлены на рис. 2.7. Система с пропорциональным PC (штрихпунктирные кривые) имеет статическую ошибку

Vc--,---1с. (2.44)

Тм2 «у

Максимальное динамическое отклонение скорости в системе с ПИ-регулятором при ступенчатом или экспоненциальном изменении р-с с постоянной времени Тп будет

Тм2 -у q 4>у

(2.45) Т,,фу

коэффициент, учитываю-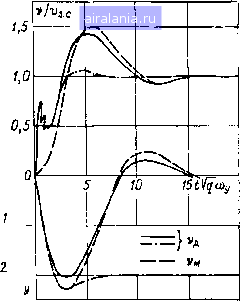

Рис. 2.7. Нормированные переходные характеристики СЭП

щий характер изменения р,с и оп- Tj\fFw ределяемый по номограмме, изобра- женной в верхней части рис. 2.6. ]ь7

Таким образом, динамика оптимизированной системы с упругой связью определяется не малыми постоянными времени, как это

имело место в жесткой системе, а параметрами механической части привода.

Параллельная коррекция СЭП. Параллельная коррекция систем с упругими связями может быть выполнена различными способами как с прямым, так и с косвенным измерением регулируемых параметров [21, 25]. При Г„. д<Гм наиболее простым и эффективным способом является введение дифференцирующих отрицательных обратных связей по скорости двигателя, поскольку при таком соотношении параметров амплитуда упругих колебаний якоря двигателя превосходит амплитуду колебаний механизма. Указанный в работе [21 ] способ сводится к включению гибкой обратной связи (ГОС) на вход регулятора тока якоря (РЯ) (см, связь, показанную на рис, 2.4, а штрихпунктирной линией). Корректирующее звено имеет передаточную функцию

к2(р)==Рк

ТкР ТкР -f 1

(2.46) 71

и выполнено с помощью отдельного операционного усилителя, работающего в пропорционально-дифференциальном (ПД) режиме.

Более простым и надежным является введение ГОС на вход PC, что позволяет исключить дополнительный усилитель и реализовать коррекцию с помощью пассивной iC-цепи (см. рис. 2.6) [59]. Поскольку PC имеет ограничение по выходному напряжению, то предлагаемый способ не приводит к срабатыванию защиты ЭП при помехах в контуре коррекции.

Выходное напряжение PC определяется уравнением

(2.47)

Г.. = (З.С-1>Д,с) (Р)-Удк1 (р).

Wi(p) = p,

TiP-f 1

г., (р) Мм±Л.

(2.48)

Tip Tl (ТкР + 1)

Pi = o/3) Рк~о/з» Ti = i?oCol Тк = ?зСз. в соответствии с последним уравнением ГОС может быть перенесена на вход токового контура, что позволяет синтезировать ее параметры частотным методом и провести сравнительный анализ различных видов параллельной коррекции. Параметры корректирующей связи целесообразно выбрать в соответствии с условиями:

= (V2 -г 2 JT] xTMSo)/,

Тк = (0,5-г-1)/о}у,

чтообеспечивает эквивалентный коэффициент демпфирования резонансного пика ЛАХ объекта % 0,7, т. е. оптимальное подавление упругих колебаний. ЛАХ /С-коррекции показана на рис. 2.6. Для формирования соответствующих характеристик объекта регулирования необходимо выбрать постоянную времени фильтра ДС по формуле 7д.с = (У у)"-

Параметры П- или ПИ-регулятора скорости выбираются по условиям (2.43), что обеспечивает настройку контура скорости на ОМ или СО. При этом частотные и переходные характеристики системы будут близки к таковым при последовательной коррекции с использованием активных фильтров.

Из рис. 2.6 видно, что характеристики СЭП при введении ГОС на вход ПИ-регулятора скорости (сплошные кривые) и на вход регулятора тока якоря (штриховые кривые) отличаются в низкочастотной области, что обусловлено различием передаточных функций (р) и (р). ЛАХ имеет в зоне низких частот наклон -f 1, в то время как характеристика Wki идет горизонтально. Это приводит к тому, что ЛАХ имеет излом слева от частоты --- и идет горизонтально на уровне 20 Ig • При при-

менении пропорционального PC Fi (р) = (р), т. е. частотные характеристики системы в обоих случаях совершенно идентичны (см. характеристики, показанные штрихпунктирными линиями),

Следует заметить, что при необходимости можно избежать потери астатизма системы в низкочастотном диапазоне и при использовании ПИ-регулятора скорости, если на его вход ввести дифференцирующую /?С-цепь второго порядка, имеющую наклон ЛАХ +2 в зоне низких частот.

Сравнительная характеристика последовательной и параллельной коррекции. Анализ полученных результатов показывает, что степень подавления упругих колебаний и реально достижимое быстродействие СЭП при последовательной коррекции с использованием активных фильтров и при параллельной /С-коррекции при-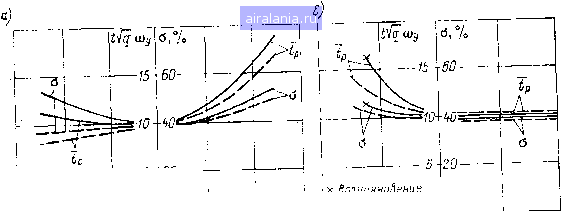

, Последовательная

коррекция

--Параллельная коррекция

I I i...-

адтокалвдании

20 kO

О 50 Д«)у,7,

Рис. 2.8. Номограммы параметров переходного процесса

близительно одинаковы. Рассмотрим возможности этих способов в условиях изменения параметров СЭП. Ряд параметров системы может изменяться как с течением времени, так и в зависимости от режима работы. В частности, подвержены изменению: коэффициент передачи тиристорного преобразователя т. п (ДО ± 50% от среднего значения при изменении скорости ЭП в 3-5раз), момент инерции механизма в ходе намотки обрабатываемого материала или других технологических факторов, частота упругих колебаний соу при износе или ремонте элементов механической передачи.

Изменение т. п влияет главным образом на динамику токового контура. При построении АСР с быстродействующим токовым контуром и относительно «вялым» контуром скорости, что и имеет место в системах с упругими связями, изменение динамики токового контура мало влияет на переходные процессы в системе как с последовательной, так и с параллельной коррекцией.

Изменение /м. а следовательно, и при постоянстве других параметров СЭП приводит к параллельному сдвигу ЛАХ Wi разомкнутой системы. В системе с пропорциональным PC переходный процесс по скорости при увеличении Ты станет более затянутым, а при уменьшении - более колебательным, В системе с пропорционально-интегральным PC, настроеннымна СО, переход-

ный процесс по скорости как при увеличении, так и при уменьшении Тм будет более колебательным, что в конечном итоге приведет к увеличению времени регулирования при применении последовательной коррекции. При параллельной коррекции снижение приводит к меньшей деформации переходных процессов вследствие меньшего изменения фазовой характеристики фр1 разомкнутой системы в зоне существенных частот. На рис. 2.8, а представлены, номограммы, характеризующие перерегулирование а и относительное время ~-t/q (Оу переходных процессов по [управлению в системе с ПИ-регулятором при изменении Тм.

Частота соу может изменяться вследствие изменения жесткости с механической передачи, что приводит к изменению постоянных времени и Т. Однако при постоянстве q и Г, соотношение частот соу (Vmc)"" и о)а= (д/ГмГс)~ не изменяется. При увеличении соу резонансный пик ЛАХ Wi на этой частоте опускается вниз за счет фильтрующего действия самой системы, и при Шу оо характеристики СЭП приближаются к характеристикам жесткой (одномассовой) системы. Быстродействие и колебательность СЭП остаются практически теми же, что и при средней частоте упругих колебаний Шу. ср. При уменьшении Шу быстродействие системы снижается и к тому же возрастает нескомпенсирован-ный резонансный пик характеристики IFpi на частоте сОу. При снижении сОу на 60% при последовательной коррекции наступает неустойчивое состояние АСР [60], что обычно приводит к автоколебательному режиму работы системы при ограничении напряжения PC (см. гл. 3). При параллельной коррекции динамика СЭП при уменьшении сОу изменяется в меньшей степени. В частности, при снижении СОу на 60% система остается устойчивой. Соответствующие номограммы изменения а и переходных процессов по управлению при изменении Шу для обоих видов коррекции представлены на рис. 2.8, б.

Проведенные исследования показывают, что при оптимизации динамики унифицированных тиристорных ЭП с упругими связями первого рода следует использовать преимущественно параллельную iC-коррекцию, так как она обеспечивает более стабильную работу СЭП в условиях изменения параметров и, как будет показано в главе третьей, при влиянии зазоров механических передач более надежна и предельно проста. Однако для ее применения необходим датчик скорости с низким уровнем пульсаций выходного напрялсения.

Последовательная коррекция с использованием активных ре-жекторных фильтров, являясь более помехозащищенной, может быть применена в СЭП с относительно небольшим изменением механических параметров или когда высокий уровень помех в системе не позволяет ввести параллельную коррекцию. Перспективным направлением здесь следует считать использование адаптивных активных фильтров с самонастройкой частоты режекции.

2.3. ОПТИМИЗАЦИЯ ДИНАМИКИ МНОГОДВИГАТЕПЬНЫХ СИСТЕМ ЭЛЕКТРОПРИВОДА С РАЗОМКНУТЫМИ УПРУГИМИ СВЯЗЯМИ

ВТОРОГО РОДА

В различных отраслях промышленности имеется большое число агрегатов, обрабатывающих материалы ленточного (полосового) типа. К ним относятся бумагоделательные и отделочные машины целлюлозно-бумажной промышленности, непрерывные прокатные станы, текстильные машины, машины по производству синтетических пленок и др. Все эти машины можно разделить по режиму работы на непрерывно-поточные агрегаты и установки циклического действия. Это налагает свой отпечаток на построение систем ЭП и способы оптимизации их динамики. В соответствии с этим рассмотрим в отдельности динамику СЭП непрерывно-поточных агрегатов и агрегатов циклического действия.

Динамика многодвигательных СЭП непрерывно-поточных агрегатов. При выработке бумажного полотна на бумаго- и картоно-делательных машинах, стальной полосы на непрерывных прокатных станах секции агрегатов связаны единым технологическим процессом. Современные непрерывно-поточные агрегаты оснащаются, как правило, многодвигательным вентильным электроприводом постоянного тока. При этом валы приводных электродвигателей соединены с секциями упругими механическими передами (упругими связями первого рода), а сами секции связаны через обрабатываемый материал, образующий в первом приближении упругие связи второго рода [22, 62, 651. Следовательно, непрерывно-поточный агрегат представляет собой многосвязную систему, в общем случае с переменными параметрами, в которой электрические, механические и технологические факторы взаимосвязаны определенным образом. При рассмотрении такой сложной динамической системы возникают следующие задачи:

1. Количественная оценка влияния упругих связей первого и второго рода на динамику СЭП.

2. Выбор способов оптимизации динамики взаимосвязанных СЗП. При математическом описании СЭП рассматриваемых агрегатов

целесообразно использовать полученные в § 1.2 нормированные структурные схемы (НСС) электромеханических объектов управления с упругими связями первого и второго рода, дополненные структурами систем подчиненного регулирования. В соответствии с этим на рис. 2.9, а представлена НСС, включающая в себя взаимосвязанные смежные {i-1)-ю и i-ю секции агрегата. У (i-1)-й секции выделен зазор в механической передаче. На рисунке введены обозначения: - постоянные времени фильтров на входах АСР; Wp с (р), д. с (р), (р) - передаточные функции ПИ-регуляторов скорости, датчиков скорости и замкнутых токовых контуров; остальные обозначения были расшифрованы в § 1.2.

Предположим для простоты, что параметры смежных секций одинаковы. Передаточная функция разомкнутого скоростного кон-