тура i-й секции в многосвязной системе, полученная с помощью теоремы Мэзона по структурной схеме (рис. 2.9, а), может быть записана в виде

IJpiM(Р) = Wp.c(Р) 132(Р) W,,,{p) Wyi(р) U7y2(р), (2.49) Wn(p)

2kvk(p

-P+I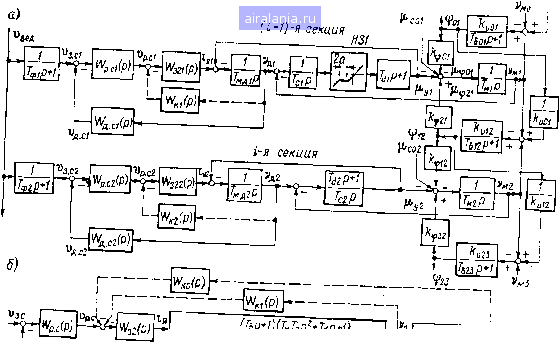

Рис. 2.9. Нормированные структурные схемы СЭП непрерывно-поточного

агрегата

С учетом выражения (2.49) НСС /-й секции может быть представлена в виде рис. 2.9, б. В приведенном выражении член Wy (р) характеризует влияние упругих связей первого рода, а Wy (р) - второго рода, которое выражается в появлении в частотных характеристиках многосвязной системы резонансных всплесков на частотах й)уо, СОу и (рис. 2.10) и соответствующих упругих колебаний в переходных процессах.

Параметры упругих колебаний второго рода, определяемые характеристическим уравнением Гуор + ЦуФ +1 = 0, соот-76

ветственно равны

Туо -

10 д/-

Частота упругих колебаний Що определяется подформуле

(Оуо =

-1 (2.50)

Гуо 2Гб V

Анализируя величины соуо и 1о, нетрудно заметить, что они зависят не только от механических и технологических факторов, но и от скорости движения обрабатываемого материала. При 8уйфГб/Гм2>1 свободное движение секций, связанных обрабатываемым материалом, носит колебательный характер; однако при превышении некоторой критической скорости движения материала v, когда SkkTT- становится равным 1, свободное движение секций будет монотонным, что может быть объяснено быстрой заменой участков деформированного материала при его движении. При

(ОсШ

Рис. 2.10. Характеристики СЭП с упругими связями первого и второго рода

относительно низких скоростях движения материала, когда бйфТб/Тмх > 1, частота свободных колебаний соу (, мало зависит от скорости полотна, приближаясь при v О к значению Шуо =

= 2kvkJ{TTQ). В верхней части рис. 2.10 построены зависимости соуо/о)*уо и IqOt v/Vii. На.рисунке видно, что демпфирование свободных колебаний, характеризуемое коэффициентом демпфирования Iq, пропорционально скорости материала.

Степень влияния на динамику СЭП упругих связей первого и второго рода определяется рядом факторов: соотношением частот СОу, СОуо, l/Te и \IT21, где Т1 - суммарная малая постоянная времени контура скорости; величиной q, коэффициентами демпфирования упругих колебаний первого и второго рода и to. а также частотой среза многосвязной системы cOcIm. Частота сом может быть определена по формуле

0)cl„==COei-. -(2.51

где ojci - частота среза локальной системы; k-= 1/(TiC0ci), Pi, Tj - коэффициент настройки, динамический коэффициент усиле-

ния и постоянная времени ПИ-регулятора скорости; - коэффициент передачи обратной связи токового контура.

В табл. 2.1 приведены условия доминирующего, или взаимного, влияния упругих связей первого и второго рода, а также приближенные оценки несущественности такого влияния, полученные при исследовании выражения (2.49) частотным методом.

Таблица 2.1

Соотиоошние частот

Доминирующее (взаимное) илнинис yiipyi-Hx связей

Условие несущественности влияния

< со

Первого poui

с- м

-Г- < «уо <

<

При соуо .<Г СОу - первого рода

При Wyo да о)у - взаимной

CMS;

"уоТб

<

<СОуо< СОу

<

Из табл. 2.1 видно, что в системах ЭП в зависимости от соотношения динамических параметров и режимов работы приводов может наблюдаться преимущественное влияние упругих связей первого или второго рода либо их взаимное влияние, причем в большей или меньшей степени. Это требует дифференцированного подхода и коррекции динамики взаимосвязанных СЭП.

Настройка динамики СЭП без применения специальных корректирующих устройств. Задачей такой настройки является подавление упругих колебаний первого и второго рода и обеспечение соответствующего качества динамики как локальной, так и многосвязной системы. В соответствии с изложенным в § 2.2 контур тока настраивается на оптимум по модулю при соответствующем выборе величины Т2-

Параметры PC выбираются при отсутствии натяжения обрабатываемого материала, т. е. как для локальной системы. Это обусловлено тем, что непрерывно-поточные агрегаты могут работать при отсутствии материала в период пуска секций, в случае обрыва полосы и других причин, а также при незначительных натяжениях материала. Однако и в этих режимах должна быть обеспечена устойчивая работа СЭП. В рассматриваемых СЭП регулятор скорости является чаще всего пропорционально-интегральным, что обеспечивает необходимые динамические характеристики системы при изменении момента сопротивления секции. При этом параметры PC Pi и Tl выбираются по условиям (2.41), что обеспечивает настройку локального контура скорости, близкую к настройке на симметричный оптимум (см. ЛАХ Wi на рис. 2.10), при частоте среза ы, определяемой формулой (2.42)..

Наличие натянутого упругого материала существенно изменяет характеристики контура скорости. На рис. 2.10 представлены амплитудные Wpu, и фазовые фр1м характеристики разомкнутого скоростного контура в многосвязной системе, построенные по выражению (2.49) на нижней (сплошные кривые) и верхней (штрихпунктирные кривые) скорости ЭП при диапазоне регулирования Д = 10. Характеристики рассчитаны для типового сочетания параметров секционного ЭП высокопроизводительной бумагоделательной машины: СОу = 50 с-; ii = 0,05; q = 0,03; = 750; = 0,8; соуо = 10 c-; = 0,025; Г« = 3,1 с; Гб„ = 2 с, причем индексом «н» обозначены параметры на нижней скорости. На рисунке видно, что многосвязная система также устойчива во всем диапазоне скоростей. Здесь следует заметить, что проверка устойчивости многосвязной системы должна в первую очередь производиться на нижней скорости ЭП, при которой влияние упругости второго рода выше.

На основании формулы (2.51) с учетом выбранной настройки PC можно оценить снижение быстродействия контура скорости в многосвязной системе, характеризуемое частотой среза со.ь,, следующим образом:

JMStOy

(2.52)

Из последней формулы видно, что указанное снижение быстродействия пропорционально диапазону регулирования скорости Д. Поэтому длительность переходных процессов как по управлению, так и по возмущению может возрастать в многосвязных системах в десятки раз, в особенности на нижних скоростях приводов непрерывно-поточных агрегатов. Вместе с тем при изменении момента сопротивления в многосвязной системе наблюдается снижение максимального динамического отклонения скорости в

max л

max м

TuTtlxq

(2.53)

раз, что объясняется противодействием межсекционных связей (индексы «л» и «м» означают соответственно локальную и многосвязную системы).

Оптимизация динамики СЭП с применением специальных корректирующих устройств, при недостаточном быстродействии локальной системы или при неустойчивой работе многосвязной системы необходимо применять корректирующие звенья, эффективно подавляющие упругие колебания первого и второго рода. В предыдущем параграфе были описаны такие средства последовательной, и параллельной коррекции (активные режекторные фильтры, JC-коррекция). Эти же корректирующие звенья применимы и в многосвязной системе.

Для подавления влияния упругости первого рода возможно применение как активных фильтров, так и iC-коррекции (см. корректирующее звено (р) на рис. 2.9, б), причем с параметрами, рекомендованными для локальной системы [см. условия (2.48)], что обеспечивает оптимальное подавление упругих колебаний первого рода и в многосвязной системе во всем диапазоне рабочих скоростей привода. В соответствии с рекомендациями, изложенными выше, применение iC-коррекции в большинстве случаев оказывается предпочтительным.

Параметры ПИ-регулятора скорости выбираются для локальной системы в соответствии с формулами (2.43), что обеспечивает настройку локального контура скорости на СО при частоте среза Cci - 0,5 -sjq СОу.

Используя выражение (2.51) для рассматриваемой настройки PC, можно оценить снижение быстродействия скоростного контура в многосвязной системе по формуле

(2.54)

откуда следует, что это снижение пропорционально А. Наряду с этим в многосвязной системе наблюдается снижение динамического отклонения скорости при возмущении ,Ueo в,

(2.55)

раз.

Анализируя формулы (2.52) (2.55), можно заметить, что в системе без специальных корректирующих устройств «удерживающее» влияние межсекционных связей через обрабатываемый материал проявляется в значительно большей степени, чем в системе с корректирующими устройствами. Следствием этого является удовлетворительная работа непрерывно-поточных агрегатов при натянутом материале, несмотря на недостаточное в ряде случаев быстродействие локальных контуров скорости. Однако, и практика подтверждает это, заправка материала на таких агрегатах оказывается 80

весьма трудной задачей, что приводит к увеличению времени холостого хода агрегатов. Следовательно, быстродействие локальных * СЭП должно выбираться исходя из условия обеспечения допустимого удлинения (натяжения) обрабатываемого материала при воз-можных (или типовых) возмущающих воздействиях.

В системах ЭП с широким диапазоном регулирования скорости может наблюдаться существенное влияние упругости второго рода, в особенности на нижних скоростях, приводящее к появлению в АСР упругих колебаний с частотой соуо. Это возможно, в частности, при сочетании параметров ЭП, соответствующем третьей строке табл. 2.1. Поскольку попытки одновременного подавления упругих колебаний первого и второго рода с помощью корректирующего звена {?) (см. рис. 2.9, б) обычно не приводят к успеху, то для подавления влияния упругости второго рода необходимо применять отдельные корректирующие звенья. В качестве параллельной коррекции может быть использована гибкая отрицательная обратная связь ip), вводящая реальную производную по скорости механизма на вход регулятора тока или скорости. Передаточная функция корректирующего звена будет

Wko{P) = PkO

ТкоР

(2.56)

ТкоР + I

и в первом случае оно строится на отдельном операционном усилителе, работающем в пропорционально-дифференциальном (ПД) режиме. Во втором случае возможно использование пассивной 7?С-цепи второго порядка, включенной на вход PC. Параметры корректирующей связи целесообразно выбирать по формулам:

г. 20л/2"„у, . ] .о

Рко----у - -г-, У.П

ГбСОуо ЮСОуо

что обеспечивает оптимальное подавление упругих колебаний второго рода. Недостатком предложенного способа коррекции является необходимость установки датчика скорости на валу механизма, что не всегда возможно. Тогда для подавления упругих колебаний второго рода можно включить на выходе PC активный режекторный фильтр, настроенный на частоту соуо. Удовлетворительная работа фильтра будет зависеть от стабильности сОуо. При этом для подавления упругих колебаний первого рода должно быть использовано активное ПД-звено, вводящее производную по скорости двигателя на вход регулятора тока; параметры ПД-звена определяется условиями (2.48).

Управление скоростью агрегатов. При управлении скоростью не прерывно-поточных агрегатов с помощью изменения ведущего напряжения Ивед (см. рис. 2.9, а) возникает задача оптимального согласования скоростей смежных секций при максимально допустимой скорости изменения ивед- Для этого на вход СЭП секции, имеющей наименьшую частоту среза со!, включается апериодический фильтр первого порядка с постоянной времени Тфх =