

|
|
Главная -> Математическое описание сэп 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 [19] 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 казали, что попытки повышения быстродействия АСР за счет увеличения коэффициента усиления PC приводят к возникновению в СЭП незатухающих колебаний регулируемых величин. Частота колебаний на тяжелых секциях БМ составила в среднем 7-8 Гц, на легких секциях 11-13 Гц. При этом частота колебаний практически не зависела от скорости БМ. Напряжение на выходе PC u, периодически изменялось от минимального (t/p. с л* 0) до максимального (t/p.co) значений, обусловленных уставками блока ограничения напряжения PC. На ряде секций БМ наблюдались «стук» редукторов и повышенное искрение на коллекторах приводных двигателей. Поэтому возникла задача исследования причин такого режима работы приводов и выбора соответствующих средств коррекции, подавляющих колебания в нелинейных АСР. НЗ} !-----\тг---- г 4dp) Рис. 3.1. Нелинейная НСС электроприоода с упругой связью первого рода Автоколебания в СЭП при ограничении PC. На рис. 3.1 представлена НСС электропривода с учетом ограничения выходного напряжения PC и наличия зазора в механической передаче. Ограничение напряжения PC структурно представлено нелинейным звеном н31 типа «ограничение», характеристика которого при записи уравнений в относительных отклонениях переменных располагается симметрично относительно начала координат и имеет наклон 45° к оси абсцисс. Нагруженный моментом сопротивления зазор в передаче представлен смещенной характеристикой типа «зона нечувствительности». Соответствующие обозначения на рис. 3.1. были объяснены в § 1.2. Исследуем возможности возникновения автоколебаний в СЭП с упругой механической передачей (упругой связью первого рода) при ограничении выходного напряжения PC. Будем вначале считать, что зазор в передаче не влияет на динамику системы. Исследование проводим методом гармонического баланса применительно к логарифмическим частотным характеристикам [17, 51]. В соответствии с этим методом система представляется в виде линейной части с передаточной функцией wpi [р) и нелинейного звена н31 типа «ограничение». Передаточная функция wx полученная с помощью теоремы Мэзона по структурной схеме (рис. 3.1) при прене- брежении обратной связью по ЭДС двигателя, будет Wp. с (Р) Цз2 (Р) д. С (Р) (ТмТсР + + 1) 7м2Р(ЛПр+7Р + 1) (3.1) При исследовании условий возникновения автоколебательного режима работы в такой системе, а также частоты автоколебаний (i)ai и амплитуды первой гармо- ники Ла1 на входе звена н31 , воспользуемся логарифмическим I критерием устойчивости нели- 20 нейных СЭП. Условия гармонического баланса при однозначной нелинейности, каковой и является характеристика типа «ограничение», записываются в виде 20 Ig (0)) = 20 Ig g{a) Ф (со) = -л. (3.2) Одновременность выполнения указанных условий заключается в том, что точки пересечения логарифмических амплитудных характеристик линейной части системы 20 Ig w (ю) и нелинейного элемента 20 Ig- и их sia) фазовых характеристик ф (to) и - л; лежат на одной вертикали. Нормированные логарифмические характеристики СЭП построены на рис. 3.2. До тех пор пока резонансный пик ЛАХ 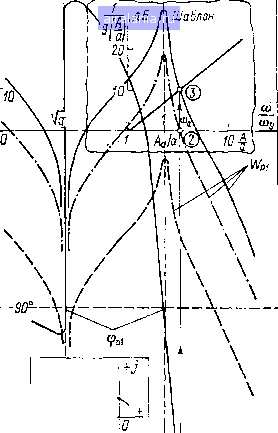  ® Рис. 3.2. К определению параметров автоколебаний при ограничении выходного напряжения регулятора скорости на частоте упругих колебаний © у ра спсложен ниже оси со/соу (см. характеристику, показанную штриховой линией), система регулирования устойчива. Предположим далее, что за счет увеличения динамического коэффициента усиления Pi PC характеристика начинает подниматься вверх. В результате наступит положение, при котором система окажется на границе устойчивости (см. штрих-пунктирную характеристику Upi), поскольку при частоте среза ЛАХ в точке 2 фазовая характеристика фр1 пересекает горизонталь - 180° и запас по фазе равен нулю. При дальнейшем подъеме ЛЛХ линейная система станет неустойчивой (см. характери- стику, показанную сплошной линией). Очевидно, ограничение выходного напряжения PC должно при этом привести к автоколебательному режиму работы СЭП. Для проверки этого воспользуемся графическим способом определения частот и амплитуд колебаний в нелинейных системах (методом шаблонов) [51 ]. Наложим шаблон амплитудной характеристики нелинейного звена типа «ограничение» на логарифмические характеристики линейной части системы таким образом, чтобы ось шаблона А!а совпала с осью со/соу, а точка пересечения характеристик IFpi и и точка пересечения фазовой характеристики фрх с отметкой -180° находились на одной вертикали. Это положение шаблона показано на рис. 3.2 и является графическим решением уравнений гармонического баланса (3.2). По шаблону определяется отношение AJa, а по характеристике Wx - частота колебаний dual. Для выяснения вопроса о том, являются ли данные периодические колебания устойчивыми, т. е. автоколебаниями, следует воспользоваться критерием устойчивости автоколебаний. Для этого уравнение гармонического баланса W{m)J{Ala)-\, (3.3) которое при однозначной нелинейной характеристике имеет вид g{A!a) (3.4) решается графически. Графическое решение уравнения для рассматриваемого случая представлено в нижней части рис. 3.2. Точка м пересечения характеристик Wpi (/со) и ---является g{Ala) точкой устойчивых колебаний (автоколебаний), поскольку характеристика (/со) не охватывает точку, расположенную на ха- рактеристике - и соответствующую увеличенной ампли- g{Ala) туде А. Следовательно, в неусд-ойчивой СЭП с упругой связью первого рода будет наблюдаться автоколебательный режим работы, вызванный нелинейностью статической характеристики PC. Выходное напряжение PC будет периодически изменяться от минимального до максимального значения с частотой coai, причем частота автоколебаний coai несколько выше частоты свободных упругих колебаний соу механической системы. Этим, в частности, и объясняется то, что в СЭП легких секций бумагоделательных машин, имеющих большие значения сОу, частота автоколебаний оказалась выше, чем в СЭП тяжелых секций БМ. Интересно отметить также, что возникновение автоколебательного режима работы СЭП при ограничении выходного напряжения PC возможно и в жесткой системе или в системе с упругой связью, у которой резонансные всплески характеристики Wpi подавлены тем или иным способом. Действительно, при достаточном увеличении коэффициента усиления PC система станет неустойчивой, что Приведет к автоколебательному режиму при ограничении выходного напряжения PC. Определение амплитуды Ла и частоты соа автоколебаний производится аналогично изложенному выше. Характерно, что в данном случае значение сОа обусловлено, по существу, малыми постоянными времени СЭП (постоянные времени фильтров), в то время как в системе с упругой связью cOai определяется главным образом параметрами механической части привода, в частности частотой упругих колебаний соу. Рассмотрим условия вхождения в зазор в автоколебательном режиме предварительно напряженной моментом статической нагрузки Лс механической системы. Для этого необходимо определить максимальное отклонение упругого момента fXy, что может быть сделано на основании рис. 3.1 следующим образом. Зная амплитуду автоколебаний Лаь можно последовательно найти амплитуду автоколебаний регулируемых величин ид. с, Vfl, v„ и [Ay. В результате получим общую формулу, удобную при теоретических расчетах: (3.5) ~Гр.е(С0а.) Гд.е(С0а.) где \»7р., (coai), IJa.c (tuai), \\7д. coai) - соответственно значения амплитудно-частотных характеристик PC, датчика скорости и механической системы на частоте cOai; при этом передаточная функция напряженной механической системы Vm (р) Тр 1 д. м (Р) - Vд (р) ТТ,р->гГр + 1 (3.6) при экспериментальных исследованиях удобно пользоваться формулой , ч д.с(сОах) Wfl.m(cOai) Тм(Иах полученной из выражения (3.5) путем замены (3.7) А, " Wp.c(cOai) = Уд.с(а1). Значение амплитуды автоколебаний напряжения датчика скорости (тахогенератора), рд. с (cai) определяется с помощью осциллографа. Если ру < 1, то автоколебания происходят без влияния t.ncpa; если Ру>1, то механическая система входит в зазор, что и вызывает «стук» редукторов. Необходимо отметить, что автоколебательный режим крайне неблагоприятно влияет на работу как механической, так и электрической части приводов, вызывая снижение точности регулиро-нания и ухудшение условий коммутации двигателей, а также пере- напряжения в механических передачах и преждевременный износ валов, муфт, редукторов. Для устранения автоколебаний, обусловленных ограничением выходного напряжения PC, возможно применение рассмотренных выше специфических средств последовательной и параллельной коррекции (активные режекторные фильтры, iC-коррекция), подавляющих резонансный пик ЛАХ объекта регулирования на частоте упругих колебаний сОу. Экспериментальные исследования вентильных приводов БМ подтвердили такую возможность [59 J. Автоколебательные режимы оптимизированных систем электропривода с нелинейной упругой связью. Весьма важным является определение возможности возникновения автоколебаний в (2ЭП, когда параметры регуляторов и специфических средств коррекции выбраны оптимальным образом для линеаризованной системы. Такая возможность обусловлена тем, что наладка систем электропривода нередко проводится в условиях, отличных от условий при последующей эксплуатации. В частности, вследствие широкого изменения момента сопротивления возможно существенное влияние зазоров механических передач в определенных режимах работы СЭП. При дальнейшем анализе будем считать, что регулятор скорости работает в линейной зоне своей характеристики. Это дает возможность выделить влияние зазора в чистом виде. Рассмотрим вначале случай применения активного режектор-ного фильтра (АФ), включенного на выходе PC. Анализ автоколебательных режимов производится с помощью метода гармонического баланса. В рассматриваемом случае система (см. рис. 3.1) представляется состоящей из линейной части с передаточной функцией (р) и нелинейного звена Н32 с характеристикой типа «зона нечувствительности». Передаточная функция Wjii (р), полученная при свертке контуров НСС (рис. 3.1), будет (Р) \УР.С.Э(Р) (Р) -Д.с(Р) ТиТсР 1 4. C.3{P)WS,{P) ЦД. с(Р) Тм.дР Цр. с. э (Р) (р) Гд. с (р) Тм1,Р , л, ЦР.с.э(р)Гз,(р)Гд.с(р) 7м2Р (3.8) где IFp. с. э (р) - эквивалентная передаточная функция PC и АФ-Положение нелинейной характеристики звена Н32 определяется углом скручивания 0 упругой передачи, нагруженной моментом Мс. При исследовании условий возникновения автоколебательных режимов в такой системе, а также для определения частоты автоколебаний Юа и амплитуды первой гармоники Ла на входе 8Вена Н32, как и выше, воспользуемся логарифмическим критерием устойчивости нелинейных систем. При однозначной нелинейности, каковой и является характеристика «зона нечувствительности», условия гармонического баланса записываются в виде (3.2). Соответствующие нормированные логарифмические характеристики СЭП построены на рис. 3.3. Амплитудная характеристика линейной части системы Wjii имеет наклон -2 (-40 дБ/дек) в зоне низких частот и характерный резонансный пик в зоне существенных частот; характеристика имеет резонансный провал ниже - 180° слева от частоты ©у. Вид амплитудной характеристики нелинейного звена Н32-опре- деляется отношением \xja. Для определения частот и амплитуд колебаний в системе удобно использовать метод шаблонов. При этом шаблон амплитудной характеристики нелинейного звена типа «зона нечувствительности» накладывается на логарифмические характеристики линейной части системы, как это изложено выше. Такое положение шаблона, показанное на рис. 3.3, и является графическим решением уравнений гармонического баланса (3.2). По шаблону определяется отношение AJa, а по характеристике Wj:i - частота колебаний о)а. Для выяснения вопроса о том, являются ли эти колебания автоколебаниями, необходимо решить графически уравнение гармонического баланса (3.4). Соответствующее решение уравнения для данного случая представлено в левой части рис. 3.3. Анализ построений на рис. 3.3 позволяет сделать следующие выводы: при Мс = О (liJa = 0) в системе будут автоколебания в точке Q с амплитудой Лаг и частотой соаг; 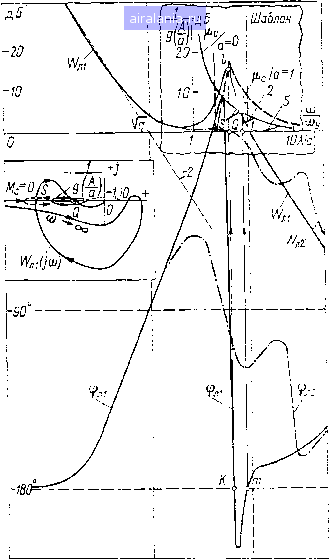 Рис. 3.3. К определению параметров автоколебаний при влиянии зазора механической передачи 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 [19] 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0.009 |