Урав1[ение (1.7) станет

1Де k, -..кф

в. с

(1.11)

Д. с

Уравнение (1.10) с уче™м (..И) «ожет быть переписано,-

После подстановки уравнения (1.12) в (1.8):получим

(1.12)

- в. / ,

(1.13)

где / в. т = в f -постоянная времени контура вихревых

Ак В. С

токов.

Подставляя уравнение (1.13) в (1.9), имеем

W в. тР -г U

где --постоянная времени основного потоко-

в в, с

сцепления.

После приведения к общему знаменателю уравнение (1.14) может быть записано как

в (Тв. тР + 1) = ьв [Г.Тз. + (Гв о + 7. + Гв. т) р + 11 -kpT. оР1я.

(1.15)

Распределение корней уравнения Тв.трз + (Тв. о + + + Тв. т) р + 1 обычно таково, что можно пренебречь слагаемым TsTq.jP. с учетом этого выражение (1.15) примет вид

1)в (Та. тР + 1) - 1в [{Т + п. т) Р + 11 -рГв. оР1я, (1.16)

где = Гв.о + Г.

Постоянная времени Tg обычно учитывается коэффициентом рассеяния = 1,15ч-1,25. Тогда

7в = сг.Гв.о-аз ff"" • (1.17)

АВ В. С

Иногда кривая намагничивания машины задается в виде Фд = = /(/вШв. п). причем Ша.п -число ВИТКОВ обмотки возбуждения на полюс; = 2р1ю,\ р„ - число пар полюсов. В этом случае

с 2d tti Ф

Г.=а,-А гЛ, (1.18)

АВ В. С

где Св = в/Шв.п - коэффициент пропорциональности между по-16

током и МДС, определяемый тангенсом наклона касательной к кривой намагничивания Фд = f (/вв. п)-

Уравнение (1.16) окончательно может быть записано в виде

1.=--ZVrP±i Z, (1.19)

где Гв.э = Т,

в. т

73. эР + 1

эквивалентная постоянная времени воз-

буждения машины.

Определим теперь связь между ц и фд в динамике. Из формулы (1.10) с учетом (1.11) следует

LkTb.tPV (120)

После подстановки уравнения (1.20) в (1.8) имеем

Гв. тР + 1

фд ~"" в -

Гв.тР -Ы

(1в -Vh).

(1.21)

Следует отметить, что нормированные постоянные времени Ts, ?», т. Гв.о, Гв и Гв. э в уравнениях, записанных для относитель, ных единиц, равны таковым в уравнениях, записанных в абсолютных единицах, что предопределяет физическую наглядность и удобство экспериментального определения параметров электрической мшнины.

Уравнения механической части электропривода. Кинематические ixtMbi механической части ЭП промышленных агрегатов могут быть весьма сложными, состоящими из нескольких инерционных масс, спизпиных валами, муфтами и редукторами. При этом возможно последовательное, параллельное и смешанное соединение кинематических звеньев механических передач. Для математического <ин1саиия многомассовых систем обычно используют расчетные схемы, в которые входит несколько сосредоточенных инерционных мпсс Jl и соединяющих их безынерционных упругих механических t ии1(»й, имеющих некоторые приведенные значения коэффициентов мисткости Ci, внутреннего демпфирования Ьс и зазора 2f, В ряде i.iVM.ien в расчетных схемах учитывают и внешнее демпфирование ПИ, обусловленное наличием сухого трения, ветрового сопротив-tnmii и другими факторами.

I.к смотрим вначале последовательное соединение звеньев ме-*.1»ч кой передачи (рис. 1.4). При составлении дифференциальных \i(iimeHHi"i движения многомассовой механическо системы исполь-iVM и принцип Даламбера и предполагается, что силы и моменты, нуи)1цие на систему, приложены в местах сосредоточенных МММ, п упругие деформации подч11§нь1 закону Гука. При работе

Му,=

механизма в установившемся режиме с моментом сопротивления зазор выбран и вал находится в скрученном состоянии, соответствующем приложенному моменту М. При зтом следует различать угол рассогласования координат кон доведанного упругого звена бр и угол упругого скручивания звена дус] образуемый после выбора зазора Zi. С учетом изложенного исходные дифференциальные уравнения равновесия расчетной п-массовой системы имеют вид

Mg-Лу1 = УдроЗд; (1.22)

-- Ч-ЬхКсОд-(Oi) при

р 10ci4-i<-ер1<есь (123)

-М при Эс1<-GpiOci + Si;

Myi-Aly2 = /]pcui; (1.24)

Му;(„ ]) -Мс=«/мРС0м, (1.25)

где - угол упругого скручивания данного звена передачи при моменте сопротивления механизма М- При переходе к относительным значениям переменных уравнения (1.22) - (1.25) могут быть записаны в виде

1д~[Ху1--Г„ друд; (1.26)

Иу1 =

при 1=-грра<1+2ai;

\iyl-\iy2 = Tipvi,

(1.27)

(1.28) (1.29)

где Т, д = УдСОд. JMcy Ti = У.-сод. JM, = У,(Од. JM - механические постоянные времени двигателя, промежуточных инерционных звеньев и механизма; Tt = MJ{Ci(aJ,c)\ Т,ц = bi/ci - соответственно постоянные времени, характеризующие жесткость и демпфирование упругих элементов механической передачи; Уд = = озд/шд.с; Vj = о) <Од.с; = со„/сОд..; р,д = MjIM; \iy[ =

Уравнения связи. К уравнениям связи относятся в общем случае нелинейные уравнения ЭДС и момента двигателя:

ЯдйФдОд; Л1д = Фд/„. (1.30)

При переходе к относительным величинам эти уравнения примут вид

(1.31)

при малых отклонениях переменных возможна линеаризация урнипений (1.31) в виде

Аед = Дфд + Агд; Ар.д = Дфд +А1я. (1,32)

Нормированные структурные схемы блока двигатель - меха-На основании уравнений (1.3), (1.19), (1.21), (1.26) - (1.29) и (1.31) может быть построена нелинейная нормированная структур пая схема (НСС) блока двигатель-механизм, показанная на

\fbyi

)>----0-i*0*--

Рис. 1.5. Нормированные структурные схемы блока двигатель-механизм

pin-. 1.5, а. Данная НСС является обобщенной, поскольку она со-Шржит достаточно полную информацию о характеристиках якорной цепи и цепи возбуждения двигателя, о свойствах многомассовой мг\,1пнческой системы с нелинейными упругими связями первого р>д; и пригодна для анализа динамики как «в малом», так и «в большим».

Анализ приведенной НСС позволяет сделать вывод, что /г-массо-luni механическая система имеет п частот свободных упругих коле-гтипй соуь обусловливающих появление п соответствующих резо-и.ии-мых всплесков в частотных характеристиках объекта управлении, Сгепень влияния этих всплесков на динамику замкнутой си-« MMi.i может быть определена в каждом конкретном случае с помощью построения частотных характеристик АСУ. Как правило, \ичу подлежат те резонансные частоты щс, которые деформируют **р;К11))1стики АСУ в зоне существенных частот.

При инженерных расчетах электромеханических систем часто ки шик.цг задача эквивалентирования многомассовой системы двух-м п! ipfXMMccoBofi. Для большинства практических случаев реаль-II П1 . Ill (IM.i двигатель-механизм в первом приближении может ги,1м. лиит,1лентирована трехмассовой системой, состоящей из дви-1М1.,и1. рсдуктора и механизма. Для определения в общем виде s< iKHiifi, которых трехмассовая система может быть сведена

К двухмассовой, рассмотрим напряженную моментом Цс трехмас-совую механическую систему, когда влиянием зазоров механической передачи можно пренебречь. Передаточная функция между моментом Цд и скоростью двигателя может быть найдена с помощью правила Мэзона (см. § 1.3) по структурной схеме рис. 1.5, а:

vn Wp{\ + Wu + Wu:-}-Wiv-uWiw)

l-\rWi-\-Wu+Win -f- WiWni + WiWiy + WnWiv

(1.33)

где Wup - передаточная функция прямого пути между р-д и Wl-WlJ - передаточные функции I-IV контуров схемы.

После несложных преобразований выражение для (р) примет вид

tti (Р) [Т,г {Т + Т,) (! Р + Т,,р + 1) + + {Т,1Р-г\){ТТ,,р + Т,,р + \)]х

X Г,,2Р

где Тм2 = Тм.д + 71 + Гм.

Полюсы Tl, Тз и нули То1, Тог функции (р), т. е. частоты резонансных пиков coyi = 1/Ti, (Oyg = l/Tg и провалов coqi = = 1/Toi, CU02 = l/Toa амплитудной характеристики IFj ((o), могут быть найдены при предположении малого демпфирования упругих колебаний в механической системе (при Tiz 0), что справедливо для многих промышленных ЭП. С учетом этого

где л - ТТгТаТа; ВТ, (Т + Т) + Т,Т,и

(1.35)

rp2 D

Возможности эквивалентирования трехмассовой системы двухмассовой зависят, с одной стороны, от соотношения параметров механической системы, а с другой - от настройки АСУ. При настройке АСУ без применения специфических видов последовательной или параллельной коррекции (активные полосно-заграждаю-щие, или режекторные, фильтры, /?С-коррекция) [59], когда нижняя частота упругих колебаний coyi в значительной степени подав-

пшт Ml счет ипер1шонности АСУ, как правило, можно ограничиться picCMOTiieiiMCM двухмассовой системы.

При применении специфических видов коррекции, подавляющих Шу, н [юзволнющих существенно повысить быстродействие АСУ, йлиинно второй резонансной частоты соуа может стать значительным, НТО потребует рассмотрения трехмассовой системы. Для исключе-ини этого оптимизация динамики АСУ должна быть выполнена учетом подавления частоты соуз. Определим, каково должно быть при этом соотношение частот (Иу и Wyj.

На рис. 1.6 представлена нормированная логарифмическая амплитудная характеристика Wi разомкнутой АСУ, настроенной на оптимум по модулю (ОМ) или симметричный оптимум (СО), что определяется параметрами ЭП и режимами работы агрегата. По-строение ЛАХ выполнено при

условии С0у1>1/Т21 (Tsi-

суммарная малая постоянная

времени системы), что справедливо в большинстве случаев. Ин рисунке введены обозначения Гшуг/соу! = а;(0о2/шу1 = I, utiii/(Oyi =7. Из построения характеристики следует, что

2()lg2?w- 20 Ig или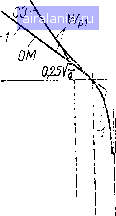

1>!

(1.36)

Рис. 1.6. Нормированная ЛАХ зомкнутой системы

где Л о - запас по амплитуде на частоте соуа (Ло чаще всего равно 2);, la--коэффициент демпфирования резонансного пика (з<0,1).

При Тм. д, Tl < Т„ и Ci > с, что нередко справедливо для электроприводов непрерывно-поточных агрегатов, значение 3 определяется по формуле

Следовательно, искомым условием эквивалентирования трех-мнссовой системы двухмассовой будет

(1.37)

а>

Переписывая (1.37) в виде

>

(1.38)