Передаточная функция замкнутого оптимизированного контура тока якоря

Фт.к(р) =

коэффициент, характеризующий ус-

где Га = Тт. п + Т, \ ловие оптимизации токового контура.

При настройке токового контура на оптимум по модулю коэффициент а = 2; при настройке на оптимум, предложенный В. Д. Барышниковым, а = 1.

Рассмотрим систему дифференциальных уравнений в операторном виде для комбинированной СЭП, составленную на основании структурной схемы (рис. 4.5, а) и представленную в матричной форме:

(4.35)

А(р)

М(р)

«14 (P) - Wp.c (P) Wo.c (p); «21 (P) = p.T (P); «23 (p) = Wp,, (P) Uo.T (P); «24 (P) = 0; Й32 (p) - (p) Wn (p);

«4з(р)=-1д(р); mn(p)=-Wp.c(p);

I2(p)-Wp.c(p) Wh(p)k.ci(p);

/?22 (P) lp.T (P) Tih (P) TiK-Tl (P); (P) = W« (p).

Передаточные функции комбинированной системы по возмущающему воздействию р будут;

при введении компенсирующей связи с передаточной функцией K.Ti (р) на вход регулятора тока [mja (р) = 0]

Ф in) = Д (Р) 22 (Р) 24 (Р) - ffl42 (Р) 44 Р)

Мс(Р) det А(р)

\<7д (р) {1 + Гр., (р) \Гя (р) lin (Р) [ Vio.T (Р) - (Р) У<и (Р)]} .

det А (р)

(4.36)

При введении компенсирующей связи с передаточной функцией к. с1 (р) на вход регулятора скорости [шаг (р) = 0]

m 12 (Р) 14 (Р) -"42 (Р) 44 (Р)

(Р) (1 + Г р., (р) (р) Г„ (р) [ \Г о., (р) - г к. с: (Р) Vip. с (Р) У*и (Р)] j

det А(р)

(4.37)

где det А (р) - определитель матрицы А (р).

Для выполнения условия абсолютной инвариантности необходимо, чтобы

ФЛр)- или Ф„(р)-0.

Из выражений (4.36) и (4.37) следует, что компенсирующие устройства должны иметь передаточные функции:

1и(р)Фт.к(Р) ttK.cl (Р)-

/гд(Гд.яР+1)

1и(р)Фт.к(р)А7р.е(р) Wp.e(p)

(4.38) (4.39)

Положим, что Гд = Гд. я, а = . Очевидно, что эти условия не нарушают общности решаемой задачи. Тогда в соответствии с выражением (4.38) получим

ip) - K.Ti («7l2p + «Г22Р + 1). (4.40)

где к. т1= т/д - коэффициент передачи КУ, в данном случае /гк.т1= 1.

Из выражения (4.40) следует, что условие абсолютной инвариантности в электроприводах подчиненного регулирования практически реализовать нельзя из-за невозможности выполнения операции идеального дифференцирования. Поэтому стремятся к выполнению условий инвариантности до е (условий квазиинвариантности).

Структура упрощенного компенсирующего устройства должна В111бираться исходя из высокого качества переходных процессов в СЭП, а также достаточной простоты реализации компенсирующих устройств в промышленных условиях. Из сравнения передаточных функций (4.38) и (4.39) можно заметить, что при использовании регулятора скорости с ПИ-динамической характеристикой введение компенсирующей связи на вход регулятора тока предпочтительнее, чем на вход регулятора скорости, из-за большей простоты реали-.чации компенсирующего устройства.

Рассмотрим возможные варианты передаточных функций компенсирующих устройств:

ltK.Tio(p) = K.Ti ГГ -1)

Ьзр2+ iiip+ 1

к..х(р)=к.п 1- + !!;-+!!; (4.42)

(5/?+ l)(TePf 1)

к.п2(р) = к.тх-; (4.43)

Wk.t13(p) = k.ti. (4.44)

Можно заметить, что реализация передаточных функций (4.41) и (4.42) в промышленных условиях сопряжена с определенными трудностями, поэтому в дальнейшем остановимся на компенсирующих устройствах, описываемых передаточными функциями (4.43) и (4.44).

Системы электропривода с косвенным измерением возмущения.

Для построения инвариантной СЭП можно использовать различные из рассмотренных в § 4.3 виды устройств косвенного измерения возмущения. На структурной схеме СЭП с косвенным измерением возмущения [рис. 4.5, а, где W.ti(p) = Wk.ci (р) = 0] устройство показано в общем виде.

1. Рассмотрим систему с УКИВ, схема которого изображена па рис, 4.2, а.

Матричное уравнение рассматриваемой системы можно записать в следующем виде:

A(p)x = B(p)f,

(4.45)

В(Р) =

Ьп О

адр) = д(р);

А (р) и X определяются в соответствии с уравнениями (4.35). При этом элементы аз (р) п а (р) матрицы А (р) в данном случае определяются выражениями:

a23{p) = w,.ApWo.Ap) [i-w,..zi{p)]; \

aM==W,.r{p)W,{p)W,,.2i{pl \

(4.46)

где Wz {р)=- " ""--передаточная функция звена УКИВ,

Гд. яР + 1

Передаточная функция системы по возмущению

Ф (п) = "Д(Р) = - 42 (Р) 41 (Р)

fc (Р) det А (р)

- (р) [ 1 + Раз (р) йза (Р)] det Л (р)

ЦД(Р){1 + Т.К(Р)[1-К.Т21(Р)])

det А(р) *

(4.47)

W.k (р) = Wp., (p);w„(p):WH(p)iWo,. (р) =

аГ22Р(Г22Р+ I)

Из условия инвариантности (р) = О [следует, что передаточная функция компенсирующего устройства имеет вид

Wk.t2i (Р) = aThp + аТгР + 1. (4.4"8)

2. Для СЭП с устройством косвенного измерения момента статического сопротивления, структурная схема которого приведена на рис. 4.3, а, матричное уравнение аналогично выражению (4.45) за исключением элементов as (р) и а (р) матрицы А (р), которые в данном случае определяются формулами:

W (П\ ИИК.Т2 2(Р)Д0(Р) 1.

. - 1+хйдо(р)

«23 (Р) = Wp.t (Р)

«24(p) = Wp.x(p) W«.,2 2(P)-

1+/гдо(р)

Примем, что fe„ = т, а Ти = Tjk = Тд. я; тогда вышерас-смотренные элементы матрицы А (р) можно записать так:

«23 (Р) = Wp.. (р) Wo., (р) [1 - w,..2 2:(Р)];

«24 (Р) = Wp.. (р) Wk.t2 2 (Р) Wo, г (Р) Г,о р.

(4.49)

Передаточная функция системы по возмущающему воздействию согласно формуле (4.47) имеет следующий вид:

Уд(р) д(р){1+ W,.k(p)[1- Гк.т2 2(р)1} fc(p) detA(p)

%{р) =

(4.50)

где Wt. к (р) определяется из выражения (4.47).

Передаточная функция компенсирующего устройства, обеспечивающая реализацию условия абсолютной инвариантности, имеет вид

Wk т. 2 (Р) = аП2Р аГгР Ч-1.

(4.51)

Таким образом, абсолютная инвариантность как в комбинированной системе, так и в СЭП с косвенным измерением возмущения достигается при одном и том же виде передаточной функции компенсирующего устройства [ср. выражения (4.40), (4.48) и (4.51)]. Со-ображения* высказанные выше относительно выбора упрощенного компенсирующего устройства, справедливы также и для СЭП с косвенным измерением возмущения.

Расчеты переходных процессов, выполненные на ЦВМ, показали практическую идентичность рассмотренных систем при отработке возмущений в виде изменения момента статического сопротивления.

при расчетах приняты значения параметров системы, характерные для секционных электроприводов современных высокопроизводительных бумагоделательных машин, а именно: Ti = 0,026 с Ф1 = 31); Tl = 0,8 с; Т = 0,09 с = 2,4); = 0,215 с; = = 6,65; П = 0,005 с; k = 3l;T = 0,215 с; = 0,063; „ = = 0,002 с; Г„ = 186 с; Гд.с = 0,03 с. На рис. 4.5, в приведены графики переходных процессов в исходной системе подчиненного регулирования и инвариантной СЭП при использовании различных типов компенсирующих устройств (КУ).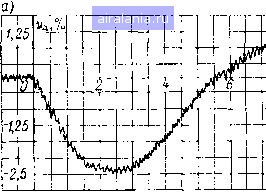

Рис. 4.6. Осциллограммы переходных процессов: а - система подчиненного регулирования; б - квазиинвариантная система

Практически устройство косвенного измерения момента сопротивления, схема которого приведена на рис. 4.2, а, может быть реализовано с помощью операционного усилителя регулятора скорости. Для выполнения условия токоограничения электропривода целесообразно компенсирующую связь по моменту сопротивления с регулятора тока перенести на регулятор скорости. При этом, если учесть, что операционные усилители системы являются инвертирующими, отпадает необходимость в введении дополнительного операционного усилителя для осуществления положительной обратной связи по току.

Принципиальная схема регуляторов скорости и тока с устройством косвенного измерения момента сопротивления и пропорциональным компенсирующим устройством показана на рис. 4-5, б.

Экспериментальные исследования СЭП с косвенным измерением возмущения, выполненные на секционном электроприводе сушиль-

НОЙ группы бумагоделательной машины Светогорского ЦБК,* подтвердили работоспособность и высокую эффективность синтезированной системы. На рис. 4.6 приведены осциллограммы переходных процессов при ступенчатом приложении люмента сопротивления в исходной (рис. 4.6, а) и квазиинвариантной с пропорциональным КУ (рис. 4.6, б) системах регулирования.

4.5. ВЫБОР ЦЕЛЕВОЙ ФУНКЦИИ ОПТИМИЗАЦИИ СИСТЕМЫ ЭЛЕКТРОПРИВОДА И ОПТИМИЗАЦИЯ ПАРАМЕТРОВ ПРОПОРЦИОНАЛЬНО-ДИФФЕРЕНЦИАЛЬНОГО КОМПЕНСИРУЮЩЕГО УСТРОЙСТВА ИНВАРИАНТНОЙ СЭП

Выбор целевой функции оптимизации системы автоматизированного электропривода является одним из важных и сложных этапов проектирования. Решение этой задачи не может быть однозначным, поскольку требования, предъявляемые к системам электропривода, весьма различны и специфичны. Можно лишь наметить подход к решению данного вопроса при синтезе СЭП с высокими динамическими требованиями на примере автоматизированного электропривода непрерывно-поточного агрегата.

Процесс оптимизации является, как правило, многокритериальным. В общем случае в целевую функцию входят технические, экономические и другие показатели. Для упрощения задачи на этапе первичного проектирования целесообразно сосредоточить внимание на технических требованиях.

Из сравнительного анализа различных критериев качества, проведенного в работе [5], можно рекомендовать для применения при проектировании СЭП интегральные квадратичные оценки вида

(4.52)

е(.)=..Р,()Ч.()%...н-Р„(-)%...

-квадратичная форма от переменных, характеризующих состояние системы.

В наиболее простом виде квадратичный критерий качества представляется в виде

2- S[v(OPd/,

(4.53)

где V (t) - отклонение регулируемой координаты от заданного значения.

* Экспериментальные исследования выполнялись, совместно с инженером Московского специализированного управления всесоюзного объедине-

ния «Союзоргбумпром» А. Г. Гузенко.