применение интегральной оценки (4.53) для нахождения оптимальных параметров системы часто приводит к получению чрезмерно колебательных переходных процессов. Для получения малоколебательных процессов используются более сложные интегральные оценки вида (4.52), в которые, как правило, входят dvldt или также dv/dt. Однако недостатком таких обобщенных оценок является более сложная связь параметров с показателем качества по сравнению с оценкой вида (4.53). Кроме того, использование интегральных и квадратичных оценок как единственного показателя качества в ряде случаев оказывается недостаточным, так как они лишь косвенно позволяют оценить качество функционирования системы. Поэтому при проектировании целесообразно использовать комбинированные критерии качества.

Для ряда непрерывно-поточных агрегатов с высокими требованиями к динамике важным критерием является максимальное отклонение регулируемой координаты от требуемого значения при действии возмущающих факторов, так как с ним тесно связаны качество выпускаемой продукции и условия нормальной работы оборудования. Например, для бумагоделательных машин таким критерием является допустимое удлинение бумажного полотна, которое однозначно связано с максимальным динамическим отклонением угловой скорости секции.

Важной оценкой качества переходного процесса является его быстрота затухания, которая влияет на износ механических передач и энергетику привода. Поэтому целесообразно использовать Б качестве целевой функции совокупность следующих функционалов качества (д, д, д): интегральной оценки /з. максимального динамического отклонения Vmax и времени переходного процесса [ip = i при котором 6 6i, Гд € бо).

Необходимо заметить, что требование минимума Vmax по возмущающему воздействию фактически является требованием инвариантности до е (или ограниченной чувствительности) к вариации внешних возмущений.

С другой стороны, следует сформулировать требования ограниченной чувствительности к вариации параметров. Например, в качестве функционала нечувствительности можно рассматривать

4 = min Yj nax I Sf {](о) I

(4.54)

где I Si (/со) - модуль функции относительной чувствительности передаточной функции системы к вариации t-ro параметра; hi - весовой коэффициент.

Таким образом, целевую функцию можно представить следующим образом:

Q = Q(f7i, 2, дз, д).

Для упрощения оптимизации по данному векторному критерию целесообразно разбить ее на два этапа:

а) вьшолнить оптимизацию по совокупности критериев д, 2. дз*

б) произвести оценку чувствительности проектируемой системы при значениях параметров, определенных на предыдущем этапе оптимизации, и выбрать их окончательные значения.

Рассмотрим подробнее критерии, используемые на первом этапе оптимизации.

Достоинством использования функционала является возможность в некоторых случаях аналитического определения «оптимальных» параметров, обеспечивающих минимум функционала, методами, разработанными А. А. Красовским. Применение функционала Уз позволяет уменьшить затраты машинного времени при решении задач многокритериальной оптимизации на ЦВМ, так как значения «оптимальных» по Уд параметров задают ориентировочную область поиска экстремума целевой функции.

Указанная выше совокупность функционалов качества, образующих целевую функцию, при, казалось бы, их внешней идентичности позволяет более эффективно организовать процесс оптимизации СЭП с высокими динамическими требованиями.

Процесс многокритериальной оптимизации может быть осуществлен путем использования следующих подходов. Первый подход заключается в том, что на основе векторной целевой функции строится скалярная функция, объединяющая в себе отдельные критерии качества. Целевая функция может быть представлена в виде линейной комбинации функционалов качества

Q = Kgi + hg2-\-hQs, (4.55)

где А,2. 3 - весовые коэффициенты.

При этом подходе возникают определенные трудности, связанные с выбором весовых коэффициентов и необходимостью нормирования отдельных функционалов качества.

В работе [431 рассмотрен один из вариантов нормализации критериев

q.= -,

(4.56)

i-cii

где д[, q\ - соответственно минимальное и максимальное значения функционала.

На начальном этапе проектирования значения q. и q\ обычно

неизвестны, поэтому данный способ нормирования нельзя считать лучшим по длительности процесса оптимизации. Другие подходы, связанные с построением массивов целевых функций при различ-

ных сочетаниях весовых коэффициентов, также нельзя считать оптимальными. Поэтому более перспективным является подход, основанный на последовательной оптимизации по ранжированным критериям качества [18].

Ранжирование критериев производится, как правило, путем экспертных оценок. Для успешного решения задачи оптимизации необходимо, чтобы множества значений параметров, доставляющих экстремум показателям качества qi, пересекались. Для выполнения этого условия приходится назначать уступки bqi на отклонение критериев качества qt от экстремальных значений.

Процесс оптимизации может быть построен таким образом, что при оптимизации необходимо назначить уступку только по одному, наиболее важному, функционалу качества. Значения уступок 6t по другим функционалам качества рассматриваются в функции 61.

В качестве критерия первого ранга при оптимизации систем электропривода непрерывно-поточных агрегатов целесообразно назначить максимальное динамическое отклонение Vmax- В качестве критерия второго ранга q следует определить интегральную квадратичную оценку У2. в качестве критерия третьего ранга - время р.

Оптимизация параметров компенсирующего устройства инвариантной СЭП. в качестве компенсирующего устройства, как отмечалось в § 4.4, может быть использовано пропорционально-дифференциальное (ПД) звено, описываемое передаточной функцией (4.43), которую в дальнейшем будем обозначать Гк.т2(р)-

Рассмотрим выбор постоянных времени т?, компенсирующего устройства, исходя из условия минимизации целевой функции.

С целью ускорения процесса оптимизации определим аналитическим путем значения параметров компенсирующего устройства, обеспечивающие минимум интегральной квадратичной оценки.

Изображение выходной координаты Л7д (/?) при действии возмущения lic [р] можно представить в соответствии с уравнением (4.47) выражением

Vb(p) = W3i(p)v,(P).

где vp) =

УЛр)- изображение регулируемой коорди-

det А(р)

наты исходной СЭП при действии возмущения (р); Wi (р) = = l-W. т2 (р) Фт. к (Р) Wy. к (р); Wy, к (р)-передаточная функция устройства косвенного измерения возмущения, определяемая согласно формуле (4.7).

Параметры регуляторов скорости и тока выбираются из условий обеспечения требуемого качества регулирования по управлению, и поэтому их можно исключить из рассмотрения при нахождении экстремума функционала У2- Тогда можно записать

Vbi(P) = W3i(p) Мр)-

Учитывая выражения (4.7), (4.34), (4.43), определим вид передаточной функции:

1.Р+1.Р+1гР + 1

1 где /з = 2 = arlatg; /3 = = aTli + tgata; /1 = аТ + Ч\ * do = aTi + Ts -T7.

В качестве возмущения примем единичное ступенчатое воздействие, являющееся наиболее тяжелым для СЭП, fXc (t) = 1 или (р) = Тогда оригинал выходной координаты системы имеет

Для вычисления квадратичной интегральной оценки целесообразно применять способы, использующие преобразование Лапласа [50].

После ряда преобразований получаем следующее выражение для интегральной оценки:

2-= -----Н

2 (аГ2 +areata+ т2)

Значения параметров т? и Xg, обеспечивающие минимум J 2, определяются из известных условий:

О;

дх-3

- -1 -I-

aTl-t-aT + xl

(4.58)

ата 2

х[2 {aT\2 + aT2, + Tlf

~\ (4.59)

Из уравнения (4.58) следует, что постоянная времени

i Л-

Учитывая, что для пропорционально-дифференциального ком-шнсирующего устройства должно выполняться условие Тд С т?, можно определить

Т7 аТг- (4-61)

Использовать выражение (4.59) в общем виде для определения тиКпия «мл.)1()й» постоянной времени Ts затруднительно. Оптималь-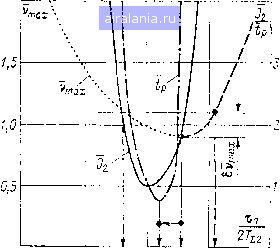

ное соотношение постоянных времени Tv/tg ПД-компенсирующего устройства можно найти, используя диаграммы качества, которые представляют собой зависимости функционалов качества от рассматриваемых параметров. Исследования показали, что оптимальные соотношения постоянных времени х/т лежат в диапазоне 7-10. При дальнейшем увеличении соотношения постоянных времени практически не наблюдается снижения показателей качества, но значительно усложняется реализация компенсирующего устройства. Поэтому при оптимизации постоянных времени ПД-компенсирующего устройства «малую» постоянную времените примем равной 0,1 «большой» постоянной времени т?.

Многокритериальная оптимизация «большой» постоянной времени производится на основании диаграммы качества,, представленной на рис. 4.7. Функционалы качества приведены на диаграмме качества в относительных единицах; Jz-JfJzal

Vrnax - Vmax/Vmaxol р~р/рО>

где J20, Vmax о» ро - базовые значения показателей качества, определенные при значениях постоянных времени т? = = 272 и Tg = 0,2 удовлетворяющих условию (4.60) при оптимизации токового контура на оптимум по модулю.

В графике критерия первого ранга Vmax = / (т?) наблюдается изменение знака максимального динамического отклонения при значении Т7> (1,3--1,4) аТ (на рисунке эта часть обозначена штриховой линией), что объясняется перекомпенсацией системы. При этом происходит значительное увеличение функционалов качества /2 и tp.

При выборе уступки 6vniax для критерия первого ранга в данном случае необходимо учитывать, с одной стороны, требования, налагаемые технологией и динамическими свойствами обрабатываемого материала на значение максимально допустимого отклонения регулируемой координаты при действии возмущений (верхний

предел 6vni£x), а с другой - допустимое отклонение от оптимума, исходя из эффективности введения компенсирующего устройства

(нижний предел fiVmax).

в результате многокритериальной оптимизации по последовательным критериям определено значение постоянной времени:

О 0,5 1,0 %5 2,0

Рис. 4.7. Диаграмма качества

(4.62)

Исследования, выполненные в работе [23], показали, что данное значение постоянной времени получается также в результате оптимизации по скалярной целевой функции вида (4.55), критерии качества которой нормированы согласно условию (4.56). Однако при оптимизации по скалярному критерию необходим большой объем априорной информации, что значительно увеличивает время поиска оптимума.

Переходный процесс для регулируемой координаты при воздействии возмущения р-с в инвариантной системе с пропорционально-дифференциальным компенсирующим устройством, параметры которого определены в результате многокритериальной оптимизации, показан на рис. 4.5.

4.6. УСТОЙЧИВОСТЬ и СТАТИЧЕСКИЕ СВОЙСТВА

АВТОМАТИЧЕСКИХ СИСТЕМ С КОСВЕННЫМ ИЗМЕРЕНИЕМ ВОЗМУЩЕНИЯ

Устойчивость инвариантных СЭП. Для оценки устойчивости инвариантной СЭП рассмотрим определитель матрицы А (р), который можно в соответствии с (4.35) представить в виде

det А (р) = 1+ «32 (Р) «43 (Р) «24 (Р) + «23 (Р) «32 (р) Нг + «21 (Р)«14 (Р)«32(Р)«43 (Р).

Элементы матрицы А (р) определяются в соответствии с выражениями (4.35), (4.46) и (4.49). Учитывая вышесделанные допущения относительно выбора параметров и Тц, обеспечивающие идентичность элементов as (р) и 24 (р) матрицы А (р) для рассматриваемых видов СЭП с косвенным измерением возмущения, определитель матрицы А (р) можно записать так:

det А (р) = 1 + (р) [I + (?-1) Wk..(Р)14- We.k(Р), (4.63)

где Wt. к (р) определяется согласно выражению (4.47); W. к (р) = =-(iP + О-ц(р)-передаточная функция скоростного

контура при разомкнутом токовом контуре; 7 = TJT - коэффициент, учитывающий вариацию механической постоянной времени привода; Тх = аТ-ч + Тд. с - суммарная «малая» постоянная времени скоростного контура; Ti - постоянная времени ПИ-регулятора скорости при настройке скоростного контура на симметричный оптимум: Tj = 4Г21.

На основании формулы (4.63) характеристический полином двухконтурной системы, скоростной контур которой настроен на симметричный оптимум, при использовании пропорционального компенсирующего устройства имеет вид

D (р) = ЬоР + Ьхр + ЬзР + ЬзР 4- + h.

(4.64) 159