

|
|
Главная -> Математическое описание сэп 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 [26] 27 28 29 30 31 32 33 34 bo = SaT%xd\ (1 -adi); = SaTidi (di-h 1 -adi); 2 --- 1 f 1 + (1 - fldi) (7 -1) K. t] ; 8ri[K.T(v-l) f 1 t-OMidzy]; 2 =д. n/S2; dl = тути 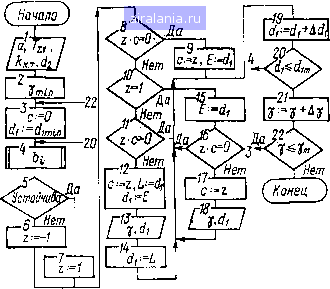 100 50 20 10 5 2 0,5 0,2 0,1)5 0,02 0,01 Область устойчивости./ Iu\d2 ~0\ 100 50 20 10 5 0,5 0,2 0x1 0,d5 0.01
0,02 OfiS 0,1 0,2 0,5 1 0Л1 0,02 0J05 0,1 0,2 0,5 1 Рис. 4.8. Структурная схема алгоритма построения областей устойчивости СЭП и диаграммы устойчивости: а - система подчиненного регулирования; 6 - инвариантная АСР Параметр d характеризует соотношение «малых» постоянных времени токового и скоростного контуров. В соответствии с прин ципами построения систем подчиненного регулирования максимальное значение параметра d- = 0,5. Для построения областей устойчивости СЭП с косвенным измерением возмущения в плоскости параметров 7 и dj воспользуемся алгебраическим критерием Рауса, позволяющим эффективно использовать ЦВМ для этих цс- лей. Структурная схема алгоритма, расчета границы устойчивости приведена на рис. 4.8. Оценка устойчивоти СЭП вьшолняется по известной стандартной процедуре и здесь не рассматривается. В зависимости от результата анализа устойчивости по критерию Рауса идентификатору z присваивается значение + 1 или - 1. При изменении знака Z на печать выводятся координаты последней устойчивой точки, если происходит переход из области устойчивости в область неустойчивости, или координаты первой устойчивой точки - при обратном переходе. Данный алгоритм позволяет находить односвязные и многосвязные области устойчивости в плоскости параметров системы. Результаты расчетов областей устойчивости представлены на рис. 4.8, а, б соответственно для систем подчиненного регулирования и инвариантной (с косвенным измерением возмущения). Потеря устойчивости в системах подчиненного регулирования происходит при 7>-1. Используя диаграммы, можно оценить рациональное соотношение постоянных времени TJT при заданном диапазоне вариации механической постоянной времени. Для инвариантной СЭП граница области устойчивости располагается при значениях 7<: 1 в случае оптимизации скоростного контура с ПИ-регулятором на симметричный оптимум. При использовании пропорционального регулятора скорости, т. е. при оптимизации скоростного контура на оптимум по модулю, СЭП с косвенным измерением возмущения сохраняет устойчивость во всей области параметров, рассматриваемой на рис. 4.8. Расширение области устойчивости СЭП с косвенным измерением возмущения при значениях 7>1 (т. е. при увеличении коэффициента передачи разомкнутой системы) объясняется тем, что частота среза системы в опрсдслен1юм диапазоне вариации 7 практически не изменяется и равна о. - l/(2T2i). Это можно показать, если рассмотреть передаточную функцию разомкнутой системы при введении компенсирующей связи, например, на вход регулятора тока при Гт.к (р) = 1: W (р)= wap) 7(4rsiP + l) 8Tl,p {аТ12РЧаТ,р + l) (Гд.,р + l) - передаточная функция разомкнутой системы подчиненного регулирования, оптимизированной на симметричный оптимум: 7д.яР + 1 Фт. к (Р) - передаточная функция замкнутого оптимизированного контура тока. [/гб Заказ № 24 Рассмотрим знаменатель передаточной функции wp. „ (р) 1 - Фт.к (р) wo., (р) + Фг к (Р) 2 (Р) (р) = 1 V р + 1 аТ%,р + аТр + \ Подставляя полученное выражение в передаточную функцию разомкнутой системы, получим 4Г2,рЧ-1 р.Лр) liP (Т ,р + 1) (Т,Т,р + Гр 4- Г) где Tl = - При 7>1 постоянная времени < Т;! и, следовательно, частота среза СЭП с косвенным измерением возмущения будет неизменной, равной ©с = l/(2T2i). Сомножитель {т-тгр -f Tjp -f 1) имеет комплексные корни, причем относительный коэффициент демпфирования данного сомножителя = VgVT с увеличением у уменьшается, вследствие чего СЭП при больших у (более 100) становится неустойчивой. Иной является причина потери устойчивости СЗП с косвенным измерением возмущения при 7<1. При 7<а/4 вышеуказанный сомножитель имеет вещественные корни; причем при у < а/4 постоянная времени Т- становится значительно больше «малой» постоянной времени токового контура Та, что приводит к появлению дополнительного отрицательного фазового сдвига в области существенных частот, являющегося причиной потери устойчивости СЭП при 7<1. Поскольку СЭП с пропорциональным регулятором скорости имеет больший запас устойчивости по сравнению с СЭП с ПИ-регулятором скорости, диапазон устойчивой работы при 7<1 несколько расширяется. Таким образом, можно заключить, что инвариантная СЭП при определенных условиях обладает эффектом адаптации к изменению коэффициента передачи звена системы с передаточной функцией д (р), входящего в устройство косвенного измерения возмущения. Из выражения (4.64) можно заметить, что при у = 1 характеристические полиномы СЭП с косвенным измерением возмущения и комбинированной СЭП совпадают. Следовательно, в определенном смысле эти системы можно считать эквивалентными как по устойчивости,"так и по обеспечению одинаковых динамических показателей. При выполнении условий инвариантности до е система с косвенным измерением возмущения является грубой, так как не вырождается порядок характеристического полинома. Статические свойства системы с косвенным измерением возмущения. Как известно, двухконтурная сэп с ПИ-регулятором скорости имеет второй порядок астатизма по управляющему воздействию и первый порядок астатизма по возмущающему воздействию При введении в закон регулирования сигнала, пропорционального Ас» измеренного непосредственно или косвенно, и при условии, что коэффициент по этой связи к.т = 1, повышается порядок астатизма СЭП по рассматриваемому возмущению до второго при использовании пропорционального или пропорционально-дифференциального компенсирующего устройства. Таким образом, в инвариантной системе можно применять пропорциональный регулятор скорости вместо пропорционально-интегрального, достигая при этом первого порядка астатизма по возмущению, необходимым условием которого является выполнение равенства к. т=1. Однако к условию повышения порядка астатизма k.j=l комбинированная СЭП и СЭП с косвенным измерением возмущения очень чувствительны, поскольку это условие реализуется при некоторых фиксированных значениях параметров системы. 4.7. РЕАЛИЗАЦИЯ УСЛОВИЙ ИНВАРИАНТНОСТИ К ИЗМЕНЕНИЮ НАПРЯЖЕНИЯ СЕТИ, ПИТАЮЩЕЙ ТИРИСТОРНЫЙ ПРЕОБРАЗОВАТЕЛЬ Сигнальный граф двухконтурной системы с устройством косвенного измерения изменения напряжения питающей сети (см. рис. 4.4) приведен на рис. 4.9, а, где использованы обозначения: Wi(p) = A;i/(Tp+l); W2{p)-h\ Ws(p)=WhP+1); 3 ~" kg/kji. Предполагается, что ЭДС тиристорного преобразователя линейно зависит от изменения напряжения питающей сети 155]. Матричное уравнение для рассматриваемой системы имеет вид (4.65) Ai(p) =
au (p) = p.c (p) o.c (p); an(p) wp., (p); «22 (p) = 1 -Wk (p) Wl(p) Wp., (p); aaa(p) = (p)W2 (p) Wp. (p); «24 (p) = (p) tt3 (p) Wp.t (p); «32 (p) = (p) Wh (p); «34 (p) = tt. (p) (p); «43 (p) = g43 (p) = Wa (p); efii(p) = p.c(p); З2(р) = 1я(р).  "Щ(р) -%(p) j
Рис. 4.9. Нормированный сигнальный граф СЭП и переходные характеристики Передаточная функция системы по воздействию U(, ф fn) Уд(Р) ЯП2(Р)34(Р) uc(p) detAi{p) gaa (Р) Яга (Р) %ч (р) det Ах(р) (4.66) где Л34 (р)-адъюнкта элемента (р) матрицы (р). Условие абсолютной инвариантности к изменению напряжения сети переменного тока выполняется при равенстве Л34 (р) - О, которое достигается при tiga (Р) = Тогда из выражения для 2 (р) можно определить передаточную функцию компенсирующего устройства: ttk (Р) = = ТкР, (4.67) Wp.t(p) i(P) где = ат-пК- Условие абсолютной инвариантности физически нереализуемо, поэтому возможно достижение только инвариантности до е при использовании компенсирующего устройства с передаточной функцией вида ki(P) = TkiP + i (4.68) Переходные процессы в исходной (кривая /) и инвариантной (кривая 2) СЭП при действии возмущения приведены на рис. 4.9, б. Применение инвариантной к изменению напряжения питающей сети системы регулирования обеспечивает значительное улучшение качества переходных процессов при отработке возмущений со стороны питающей сети: динамическое отклонение уменьшается в 6 - 10 раз, время переходного процесса - в 2-3 раза. 4.8. СИНТЕЗ ПОЛИИНВАРИАНТНЫХ СИСТЕМ ЭЛЕКТРОПРИВОДА Построение системы, обладающей свойством инвариантности некоторой регулируемой координаты к нескольким возмущающим факторам, может быть осуществлено путем объединения нескольких устройств косвенного измерения соответствующих возмущений. Рассмотрим другой подход к синтезу полиинвариантных систем регулирования, который вытекает из обобщенного топологического анализа многоконтурных систем регулирования [8]. Синтез полиинвариантной СЭП вьшолняется на основании теоремы о необходимых и достаточных условиях полиинвариантности до S выходной координаты ко всей совокупности внешних возмущений, для выполнения которых создаются дополнительные пары контуров относительно каждого из компенсируемых возмущении. При этом один из входящих в пару контуров должен быть положительным, не касающимся точки приложения возмущения ]Xi, а другой - отрицательным и касающимся точки приложения данного возмущения. Достаточные условия полиинвариантности заключаются в физической реализуемости передаточных функций звеньев, входящих в дополнительные контуры. Достаточным условием устойчивости полиинвариантной системы (при условии устойчивости исходной системы) является равенство передаточных функций положительного и отрицательного контуров, образующих пару относительно возмущения р. Рассмотрим многоконтурную систему, граф которой приведен на рис. 4.10, где применены следующие обозначения: Wpi (р), (р) - передаточные функции соответственно регулятора и объекта регулирования i-ro контура, имеющего возмущение рг, wi (р), Wii (р), Wt2 (р) - передаточные функции звеньев, образующих дополнительные контуры. G Заказ }к 24 165 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 [26] 27 28 29 30 31 32 33 34 0.005 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||