Для упрощения вида передаточной функции компенсирующего устройства Wi {р) целесообразно (если это возможно) выходной сигнал i-ro компенсирующего устройства подавать на вход регулятора последующего (внутреннего) {i - 1)-го контура.

Дополнительные пары контуров можно организовывать несколькими способами, из которых можно выделить следующие два:

а) 1-й положительный контур является не касающимся только пути передачи воздействия р

(рис. 4.10, а);

б) i-й положительный контур является не касающимся путей передачи нескольких воздействий (рис. 4.10, б).

Рассмотрим случай «а».

Передаточные функции дополнительных контуров выбираются в соответствии с теоремой следующим образом:

Wjp)

/Ьг 9 If 2

V Шр)

0-*<)-*QXs

Ш(р)

Wn(p)=Wi2(p)Woi(p);

W21(P) = WP2(P)W02(P);

Щ(р)

Щ(р)

(4.69)

Эту систему уравнений целесообразно представить у, так:

-w>

wap)

W22 (Р) = W32 (Р) =

л(Р)

03 (Р)

(4.70)

W,(p)

%iip)

-%i(p)

Рис. 4.10. Сигнальные графы полиинвариантной СЭП

Передаточные функции (р), (р), Wip) выбираются в зависимости от вида соответствующих передаточных функций объекта регулирования Wqi (р) исходя из условия обеспечения физической реализуемости и простоты передаточных функций (р), W22 (Р), (р) в соответствии с формулами (4.70).

Запишем уравнение системы в матричном виде:

A(p)x=:B(p)f,

(4.71)

А(р)-

В(р) =

о о о о о

Ьп (р) = «16 (Р) = (р); «21 (Р) - Wp2 (р); «23 (Р) = 0;

«26 (Р) = Wp2 (р) [1-8 (р) Wn (Р)1; «26 (Р) = 3 (р) (р) W32 (Р);

«32 (Р) - (р); (р) = 1 - Г р1 (р) W, (р) Wn (Р);

«34 (р) = Wpi (р) [1 - W2 (р) W2i(p) + Wi (р) Г12 (Р)];

«35 (Р) Wpi (р) W2 (р) W32 (Р); (Р) - «43 (Р) - Wol(Р);

hz (Р) «54 (Р) Wo2 (Р)> 64 (Р) - «65 (Р) Wo3 (р).

Условие полиинвариантности координаты Xg к воздействиям 11» 1а> М-з можно записать следующим образом:

Хз - Фх (р) pi + Ф2 (р) Р2 + Фз (Р) !з = 0.

Если считать, что pi, ра. з являются независимыми воздействиями, условие полиинвариантности будет выполнено при

Ф1(р) = Ф2(р)--=Фз(р) = 0. Определим передаточные функции Ф1 (р):

Ф1(Р)

Фз(р)

(4.72)

(4.73)

Из выражений (4.72) следует, что условие абсолютной инвариантности реализуется при Лв (р) = Лье (р) - Леи (р) - О, где соответствующие адъюнкты определителя А (р) равны)

Ле (р) = «зз (Р) «54 (Р) «65 (р);

Л 56 (Р) = «65 (Р) [«33 (Р) + «34 (Р) «43 (P)J; Лее (Р) = «33 (Р) + «43 (Р) «34 (Р) + «43 (Р) «54 (Р) «35 (р) + + «32 (Р) «43(Р)«54 (Р) «25 (Р).

Из последнего уравнения системы (4.73) можно заметить, что в условие инвариантности к возмущению рз (наиболее близкому к выходу системы) входят условия инвариантности к p,i и ра-Следовательно, для системы, синтезированной на основании рассматриваемой теоремы, достаточно обеспечить инвариантность выходной координаты системы к последнему возмущению, что обеспечит полиинвариантность ко всем возмущениям. Таким образом, выполнение условия абсолютной инвариантности достигается при

«зз(р) = 0; Wi(p)

аз4(р)-0; W,{p)--

«35 (Р) + «32 (Р) «25 (Р) = 0;

(Р) Wn ip)

1 + W, ip) W,,{p)

21 (P)

P2 iP) 3, ip)

(4.74)

При точной реализации передаточных функций (4.70) и (4.74) обеспечивается абсолютная полиинвариантность системы к рассматриваемым возмущениям. Приближенная реализация указанных выше передаточных функций обеспечивает полиинвариантность до £.

Покажем, что выполнение условий полиинвариантности не влияет на устойчивость системы. Для этого рассмотрим определитель матрицы А (р) для полиинвариантной системы:

det А (р) 1 + Гр1 (р) (Р) (Р) 101 (Р) 102 (Р) Wo, (р) +

+ (р) Woi (р) + Wpi (Р) Wp, (р) Woi (р) Г02 (р) +

+ (р) (р) [W,i (р) {P)-Wn (Р)] +

+ W2 (Р) Wpi (р) Г 01 (Р) [ Г 02 (Р) (Р) - 21 (Р)] +

+ з(р) \V,Ap)Wp,{p)Woi{p) о2(р)[Гоз(р) W32(P)-ll?31 (Р)].

(4.75)

При точном выполнении условия (4.70) определитель полиинвариантной системы равен определителю исходной системы, который получается из выражения (4.75) при отбрасывании последних трех слагаемых. Следовательно, полиинвариантная СЭП будет устойчива, если устойчива исходная система. Полученные выше

результаты исследования устойчивости СЭП с косвенным измерением возмущения позволяют сделать заключение о том, что и рассматриваемая система принадлежит к классу «грубых» систем. Рассмотрим случай «б».

При выборе передаточных функций дополнительных контуров в соответствии с условиями теоремы исходим из следующего:

ГХ2(Р)= "

122 (Р)-Г 32 (Р)

Wolip)

Wn (р) . 01 (р) 02 (р)

Wn (р)

Wolip) WoAp) 03 (р)

(4.76)

Уравнение системы для данного случая будет аналогично (4.71). При этом некоторые элементы матрицы А (р) определяются иначе, чем в (4.71), а именно:

«2з(р) = р2(р)з(р)и(р); «25(Р) = Р2(Р);

«33 (Р) -1 - Wpi (р) Г и (Р) [W1 (р) + W2 (р)];

«34(P)--W/pi(p)[l i-ri(p)Wi2(p)].

Определим соответствующие адъюнкты матрицы а (р): Л« (Р) = 102 (Р) Г03 (Р) {1 - [(р) + 2 (р)] Гр1 (р) X X Гц (р)- Гз (р) Wn (Р) Wpi (Р) Wpa (р)} - 0;

5б(р) = Л4в(р)Го1(р)-1 [l + Wi(p)Wi2(p)]roi(p)Wo3(p) = 0; [(4.77) Лее (Р) = Л56 (Р) Wol (р) + Woi (Р) Wo2 (Р) pi (р) X

X [Wp2 (Р) + 2 (р) Г22 (Р)] - 0.

Решая систему уравнений (4.77) относительно Wi (р), (р), 13 (р), можно определить вид передаточных функций компенсирующих устройств, но в данном случае они находятся значительно сложнее по сравнению со случаем «а». Поэтому построение полиинвариантных систем первым способом оказывается более предпочтительным.

Рассмотрим применение теоремы на примере трехконтурной системы подчиненного регулирования секционного электропривода непрерывно-поточного агрегата с общим преобразователем [59]. Сигнальный граф полиинвариантной системы представлен на рис. 4.11. а, где (р), Гц (р), Г12 (р). W, (р). (р), (р). 23 (Р) - передаточные функции элементов СЭП, с помощью которых образуются дополнительные контуры регулирования.

Возмущениями, действие которых компенсируется, являются вариация напряжения сети переменного тока, питающей тиристорный преобразователь, и изменение момента сопротивления

нагрузки Рс- Компенсация изменения напряжения общего преобразователя Do не рассматривается, так как ее целесообразно выполнить в системе регулирования напряжения общего преобразователя.

-Wo.„(p)

\v(p)/w2,(p)

)ц-&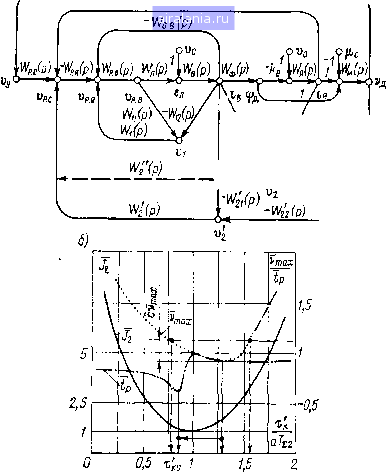

Рис. 4.11.Нормированный сигнальный граф СЭП с общим преобразователем и диаграмма качества

Дополнительные контуры регулирования относительно возмущения Рс можно образовать двумя способами:

а) используется информация о токе ц и скорости Уд, которая передается через элементы с передаточными функциями W21 (р), 22(Р);

б) основными являются связи по току 1я и скорости Уд с пере-

даточными функциями Ws (р), W22 (р). Но так как в точку приложения рс поступает прямое воздействие фд, то для его компенсации используется дополнительная связь по току ц с передаточной функцией 121 (р).

Запишем уравнения, из которых определим передаточные функции дополнительных связей:

относительно воздействия

W12 (Р)

Wu (Р)

Wn (Р) (Р)

относительно воздействия Рс

(Р) =

Г22(Р)-

ф(р) WuiP)[\-keW{p)] 23 (Р) ,

WuiP)

(4.78)

(4.79)

(4,80)

Wll (Р) = 1Гф (р) Wm (Р) W"22{P).

Передаточные функции W (р), W21 (р), w23 (р) выбираются из условий физической реализуемости и простоты передаточных

функций Wi2(p), W22{p), W22{p).

с учетом вышесказанного примем следующие передаточные функции:

Wn (Р) -

W2 (р)

ТпР+1 ТггРЛ- 1

(4,81)

где Гц = Гв. э + 7",, Ти. э. 721 Tjj T,j. т.

В соответствии с уравнениями (4.78) - (4.81) определим остальные передаточные функции дополнительных элементов:

(Р) -

W22 (Р) -

Гв.тР+ 1

(т;,р + 1)(1-г»

2 (Р)

723р+1

(4.82)

где /12 = ц/п; h2 = hxTJih {КК - 1)1; 21 = в2з; 22 =

= 2зм; =Тя/(ея-0; 21 = + Тв.Т22 = Тя; Т21 = - т23 + Тз. т - соответственно коэффициенты передачи и постоянные времени дополнительных звеньев.

Неопределенными на данном этапе синтеза инвариантной системы являются параметры ц, къ 23» 23. значения которых