будут найдены из условий инвариантности. Для этого рассмотрим матричное уравнение системы

Аз (р) Xi = Gi(p) Z,

(4.83)

Аз(р) =

Z= [UyUcfXcf;

«1в(р)-Гр.Лр)Го.д(р); «21(р) = Гр я(р); «24(Р)--Гр.я(р) WMWnip);

«25 (Р) Гр. я (р) [Гг (р) (Р) - Го. я (Р)1;

«26 (Р) Гр. я (Р) Г2 (Р) Г22 (Р); «32 (Р) = Wp, 3 (р);

«зз(Р) = 1-р.в(р)1(р) Wii(p);

«34 (Р) = Гр.в (р) 1Го.в (Р) + Гх (р) Г12 (р)];

«43 (р) = Гп (р) Гз (р); «54 (р)=КЩ (р) (р);

«64 (Р) = Гм (р) Гф (р); «65 (Р) = (Р); (Р) Гр., (р); g42 (Р) = Гз (р); 63 (Р) = Гм (р).

Дополнительное движение выходной координаты системы д, вызванное действием возмущений и рс. определяется выражением

д = Фи(Р)»с + Фц(Р)с.

Ф (р) Д = g42 (Р) (Р)

Ue(P) det A3 (р)

g42 (Р) {33 (Р) [Дб4 (Р) - Q54 (Р) 65 (Р)]}

det A3(р)

передаточная функция системы по возмущению

Уд(Р) Ябз(Р)Лбб(р) .uc(p) det A3 (р)

g63 (Р) {33 (Р) + 34 (Р) Q43 (Р) - Q32 (Р) 043 (Р) [24 (Р) " О54 (Р) 25 (Р)]}

det Аз(Р)

- передаточная функция системы по возмущению [х,-

Условие полиинвариантности СЭП к действующим возмущениям Vд = О можно реализовать при Л46 (р) - Лее (р) = О, что достигается соответствующим выбором передаточных функций компенсирующих устройств Wl (р) и Га (р). Адъюнкта определителя Л46 (р) = О, если

азз(р) = 0 или 1~Гр.ар)Г1(р)Г11(р)=-0. (4.84)

Для выполнения условия Лее (р) = О необходимо, как следует из передаточной функции Фд (р), чтобы

«33 (р) = 0;

«34 (Р)-«32 (Р) [«24 (Р) - «64 (Р) «25 (р)] = 0.

(4.85)

Из формулы (4.84) найдем вид передаточной функции (р), обеспечивающей вьпюлпеиие требования абсолютной инвариантности к действию возмущения со стороны сети переменного тока, питающей вентильный преобразователь:

1 Тзр

Гх (р) =

11 (Р) «р.в(р)

(4.86)

Учитывая физическую реализуемость передаточной функции Wl (р), ее можно записать при кц = Тд/Рз = aTkkj. так:

Wi(p)=--, (4.87)

где Tl - постоянная времени, значение которой будет определено ниже.

Из выражения (4,85) найдем с учетом условия (4.86) передаточную функцию Га (р):

W.(n)== Цо-в (Р) + 1 (Р) 12 (Р) + keW (р) (Р) Wp. я (Р) Wo. я (р)

Йеи5ф(р) Wh(p)U523(P)+ W2i(p)

(4.88) 173

подставляя соотношения (4.82) и (4.87) в последнее выражение I 123 (р) о и tl = гд. я = тд, получаем

a2 a,TzjTi3(J,p + Р) + а2Т22(Тв.т + Дз72з) + ТИзР + 1

(ПР + 1)

(4.89)

где аз, из - коэффициенты, зависящие соответственно от условия оптимизации контуров возбуждения и тока якоря; тз, - «малые» постоянные времени соответственно контуров возбуждения и тока якоря.

принимая в передаточной функции Wo (р) коэффициент k21 = - /гявет.я. переходим к ее упрощенному виду:

W2 (р)

(4.90)

TkiPH- 1

определим передаточную функцию компенсирующего устройства Wl ip) для второго варианта построения полиинвариантной системы [w23 (р) =7 0]. подставляя выражения (4.82) и (4.87) в (4.88) при tl = гд.я = тд.з = таз, получаем

(р)

агЧТъгТъЛТгР + Р") + 222 (Тв.т + аТъ) Р + а%Тф + 1

/г2з(И-/го)(ГзР + 1) гт.я

(4.91)

где 0 = I/I.-h); 72 = hTJ{\ + -feo)-

учитьшая физическую реализуемость передаточной функции

Wl (р) и простоту построения ку, при кз = т. я/(1 + о) можно записать

Г2(р) =

ТкаР + 1

(4.92)

очевидно, в качестве упрощенного компенсирующего устройства в обоих случаях можно рассматривать также и пропорцио-иальное ку с передаточной функцией

w;(p) = w;(p) = l. (4.93)

оптимальные значения «больших» постоянных времени пд-ком-

пенсирующих устройств и Тк, входящих соответственно в передаточные функции (4.90) и (4.92), определяются в процессе многокритериальной оптимизации.

диаграмма качества, рассчитанная на цвм для первого варианта полиинвариантной системы, приведена на рис. 4.11, б. из рисунка следует, что оптимальным значением постоянной времени пд-компенсирующего устройства является

то-0,8572. (4.94)

следует отметить, что для второго варианта построении полн-инвариантной системы диаграмма качества достаточно близко совпадает с диаграммой качества на рис. 4.11, б. кроме того, в результате многокритериальной оптимизации «большой» постоянной времени пд-компенсирующего устройства получено ее значение, совпадающее с условием (4.94),

переходные процессы, рассчитанные на цвм, показаны на рис, 4,12 при изменениях момента сопротивления р,, (рис. 4,12, а) и напряжения питающей сети (рис, 4.12, б).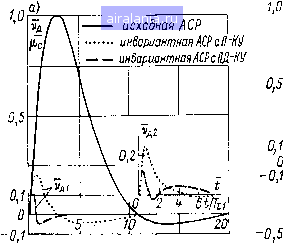

Рис. 4.12. Переходные характеристики

из анализа характеристик переходных процессов при воздействии рс можно заключить, что рассмотрен]1ые выше два варианта построения полии1шариаит11ой системы от]10сительно данного возмущения являются практически эквивалентными [на рис. 4.12

функция Уд1 (/) соответствует первому варианту, а Уд2() -второму варианту построения полиинвариантной сэп],

таким образом, синтезированная полиинвариантная система имеет высокие динамические характеристики при отработке возмущений рс и

4.9. СИНТЕЗ ИНВАРИАНТНЫХ СИСТЕМ УПРАВЛЕНИЯ ДВУХМАССОВЫМИ ЭЛЕКТРОПРИВОДАМИ С УПРУГИМИ СВЯЗЯМИ

появление в контуре регулирования скорости двухмассовой сэп слабодемпфированного звена, обусловленного упругими свойствами механической передачи, определит особенности оптимизации такой системы.

в зависимости от требований, предъявляемых к быстродействию сэп по управляющему воздействию, применяются специфические средства коррекции или используется обычный регулятор скорости со скорректированнными параметрами (при малом быстродействии системы).

Учитывая, что влиянием упругости на динамику токового контура в большинстве случаев можно пренебречь [13], компенсацию изменения напряжения сети переменного тока, питающей тиристорный преобразователь, выполняют так же, как и в жестких СЭП. Таким образом, рассмотрим особенности синтеза СЭП с упругими связями, инвариантных до е к возмущению в виде изменения момента сопротивления нагрузки. Применение специфических средств коррекции, как правило, не позволяет увеличить частоту среза системы выше значения тО,Ьл/д (Оу, где соу - частота упругих колебаний механической системы, q = J.luz - коэффициент соотношения масс. Поэтому задача синтеза инвариантных СЭП, имеющих высокие динамические свойства при отработке указанного возмущения, приобретает особый интерес и актуальность. При синтезе СЭП будем считать, что для демпфирования упругих колебаний используются известные способы коррекции [59]. Следует заметить, что параллельная коррекция в виде гибкой связи по скорости двигателя, наиболее часто применяющаяся для демпфирования упругих колебаний ввиду простоты ее технической реализации, является частью устройства косвенного измерения возмущения в двухмассовой системе (см. рис. 4.2), и поэтому могут быть использованы изложенные в § 2.2 условия оптимизации СЭП с упругими связями.

Сигнальный граф АСР электропривода с двухмассовой упругой механической передачей, содержащей устройство косвеннного измерения момента (см. рис. 4.2), приведен на рис. 4.13, а.

Система описывается матричным уравнением

А(р) =

(4.95)

«21 (р)=«26 (р)=ф.. к (р) =

«32 (Р)=«34 (Р) = Гд(р) =

«4з(Р)=«45(р) = Гс(р)= -«34 (Р) = 52 (Р) = Г, (р) =

IdP±± .

82 (Р) = Гк (р) W, (р); аез (р) Г, (р) (р); «65 (Р) = Г, (р) Гз (р);

bn{p) = W,,M; Wi(p)-А;

W2(p)-=-; Гз(р) = -;

TkiP + 1 TkiP "Г 1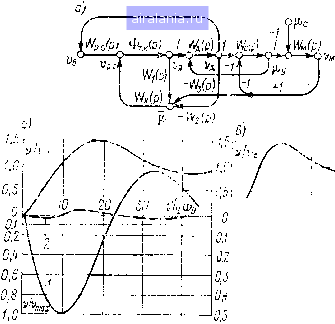

Рис. 4.13. Нормированный сигнальный граф СЭП [с упругой связью и переходные характеристики

Tl (р); Гц (р) И Гз (р) - передаточные функции звеньев устройства косвенного измерения момента; Г (р) - передаточная функция компенсирующего устройства.

В соответствии с вышесделанными допущениями будем считать, что исходная СЭП устойчива за счет корректировки параметров регулятора скорости или применения специфических средств коррекции.