можно найти

<

Обобщенные параметры С и D удобно выразить через первичные параметры механической системы:

Q

CjCiO -\-Qi-I Яг)

С учетом (1.40) условие (1.39) станет

сЯзО +91 + 9а) 02

(1.40)

<

[1+92 + йс(1 + 9з)Р(Ло + 4уа • (1-)

Это неравенство выполняется тем легче, чем при прочих равных условиях больше и меньше

Для промышленных агрегатов, у которых < 1, 2 <С 1» условие (1.41) примет более простой вид:

4Ло2 (J 42)

<

[Ц-йс(1+9з)Р " (Ло + 4у2 *

Необходимо отметить, что условия (1.41) и (1.42) выполняются для многих промышле]тых агрегатов, в частности для бумагоделательных и отделочных машин целлюлозно-бумажной промышленности, что позволяет эквивалентировать многомассовые механические системы таких агрегатов двухмассовыми системами. Опытные виброграммы свободных упругих колебаний ряда механизмов (секции бумагоделательных машин, клети прокатных станов и др.) также соответствуют двухмассовым механическим системам с линейно-вязким трением.

С учетом изложенного на рис. 1.5, б показана линеаризованная НСС двухмассовой механической системы с компенсированным электродвигателем. Следует заметить, что при Тс -> О, Т- О (т. е. при с-> оо, 6-0) рассматриваемая система становится од-номассовой (жесткой системой) с механической постоянной времени Tms.

НСС многодвигательных ЭП с упругими связями первого рода. На ряде промышленных агрегатов применяются многодвигательные электроприводы Отдельных секций (клетей). При этом рабочие валы секции связаны между собой через прижим или другую достаточно жесткую связь, а двигатели соединены с механизмом че-)ез упругие механические передачи (упругие связи первого рода). "Триводные электродвигатели могут питаться как от общего, так и от индивидуальных вентильных преобразователей.

\ Для силовой электрической части /г-двигательного ЭП с общим преобразователем могут быть записаны следующие дифференци-

ibHbie уравнения в относительных единицах [59]:

1яг =

TiP + 1 п

1я = Z •я£.

ЬФ1 п

Sn -KiVji - (ГпР + 1)2 afttW

i = l

(1.43)

где kfiki - коэффициенты, характеризующие жесткость механических характеристик двигателей; /г/j - коэффициенты нагрузок двигателей по току; Тп - электромагнитная постоянная времени силовой цепи преобразователя; ii, 1я-соответственно токи двигателей и общего преобразователя.

При питании двигателей от индивидуальных преобразователей уравнение силовой электрической части ЭП примет вид

1я =

TiP + 1

(8 nt-Л).

(1.44)

При записи дифференциальных уравнений механической части /1-двигательного ЭП в соответствии с вышеизложенным будем полагать, что каждая отдельная система двигатель-механизм является двухмассовой. При отсутствии влияния зазоров в упругих связях, что характерно для напряженных моментом нагрузки механических передач, уравнения динамики будут [59]

(1.45)

где кц{ - коэффициенты нагрузок двигателей по моменту. На основании уравнений (1.43) и (1.45) может быть построена НСС /г-дви-гательного ЭП с общим преобразователем, показанная на рис. 1.7. Данная НСС наглядно отражает многосвязность электрической и механической частей привода. Электрическая часть имеет симметричные перекрестные связи, в механической части ЭП (обведенной ттрихпунктирной линией) все электродвигатели связаны через механизм. Рассматриваемая механическая система является «-массовой и в общем случае имеет п частот свободных упругих колебаний. Следует, однако, заметить, что при Тм>Тм. д1- -массовая система распадается на «-двухмассовых систем с частотами упругих колебаний (при малом демпфировании)

(1.46)

Из последней формулы видно, что при Т„ > 7. д. с частоты ©yi не зависят от величины Гм, а определяются только инерционностью двигателей Гм.д. i и упругостью механических передач Tt.

нес с индивидуальными преобразователями может быть получена на основании уравнений (1.44) и (1.45). Данная НСС в отличие от схемы рис. 1.7 будет иметь п входов Вщ, . . . , и в ней будут отсутствовать названные выше перекрестные связи в электрической части ЭП и сумматор токов . . . , in-

Дифференциальные уравнения и НСС механической системы с упругими связями второго рода. Секции непрерывно-поточных агрегатов в общем случае связаны через вырабатываемый материал (бумажное полотно, ткань, пленка, металлическая полоса и т. д.)- рис. 1.8, а. В некоторых случаях, например на бумагоделательных машинах, ряд приводных валов охватывается замкнутым сукном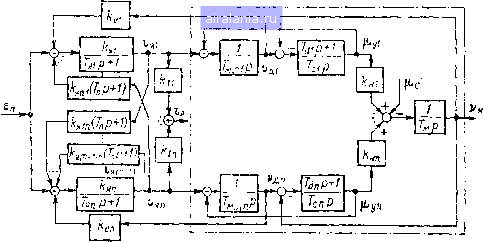

Рис. 1.7, Нормированная структурная схема п-двигательного ЭП с общим преобразователем

металлической или синтетической сеткой (рис. 1.8, б). Общим для таких связей является наличие у них упругопластических свойств. При рассмотрении динамических процессов часто идут на идеализацию характеристик указанных связей, считая их однородными, невесомыми и абсолютно упругими лентами. В этом случае зависимость между относительным натяжением ф обрабатываемого материала и разностью относительных скоростей Vm секций (приводных валов) i и i + 1 можно записать в виде [59 ]

-v„f-f---Ф, ,л

V а, i+i)

Фг. 1+1 =

(1.47)

где = ESIF - коэффициент передачи между и ф в статике; Е, S, - модуль упругости, площадь поперечного сечения и натяжение материала в статике; Tt = llv - постоянная времени удлинения материала; I, v - длина свободного участка и скорость материала.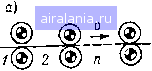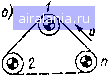

mn-i)!i

Vcon

Момент сопротивления г-й секции Met зависит как от момента холостого хода Мсои так и от натяжения материала между i, {I-1)-й и I, (г + 1)-й секциями (валами). С учетом относительных отклонений переменных уравнение равновесия моментов будет

где = Fci?p. в/(1рПрсо) - коэффициент передачи между р, ифв статике; i?p.в- радиус 1-го рабочего вала секции; tp, rip - передаточное число и КПД редуктора t-ro вала. На основании уравнений (1.47) и (1.48) с учетом уравнения меха- № НИКИ привода VYZi- ici = Tipvi (1.49)

может быть построена НСС механической системы с упругими связями второго рода, показанная на рис. 1.8, в. Рассматриваемая НСС справедлива как для разомкнутой, так и для замкнутой транспортируемой упругой ленты (материала). В первом случае связи между первой и л-й секциями размыкаются. Анализируя полученную

структуру, нетрудно заме-

тить, что при у-оо упру- гая связь второго рода вы- рождается в жесткую механическую связь. Поэтому НСС механизма на рнс. 1.7 является частным случаем структуры, пока-;шнной на рис, 1.8, при „ = оо и 7-2 Гг. /г-массовая механическая система с разомкнутыми (или замкнутыми) упру-1"нми связями второго рода имеет п частот свободных упругих колебаний (Оуо1(или (Оу зг). Степень влияния каждой резонансной мпстоты на динамику АСУ зависит от соотношения электромеханических параметров объекта и настроек регуляторов и может быть оценена количественно с помощью частотных методов. На практике нередко возникает задача эквивалентирования «-массовой

Рис 1 8. Кинематические и нормированная" структурная схемы механической, системы с упругими связями второго рода

механической системы с упругими связями второго рода двух- или трехмассовой системой. Рассмотрим вначале систему с замкнутыми упругими связями при наличии одного приводного вала. Полагается, что многомассовая система в первом приближении может быть приведена к трехмассовой, что характерно, например, для агрегатов бумагоделательного производства. Для определения условий, при которых трехмассовая система может быть сведена к двухмассовой, по структурной схеме рис. 1.8 составим с помощью правила Мэзона (см. § 1.3) передаточную функцию между моментом Цу21 и скоростью при у СЛОВИ И слзбости «прямых» связей по натяжению материала с коэффициентами передачи 1/. Тогда искомая передаточная функция будет

+ uii + "ivvi) (1 + Wl -h W,, + Wni + Wiv + lv +

+ W,W,,,Wy + W,,W,W,r\ (1.50)

где - передаточная функция прямого пути между jyi и Vmi* 1-vm - передаточные функции I -VIII контуров схемы.

При предположении равенства параметров ветвей упругой связи, т. е, при одинаковых значениях k, и Т, после ряда преобразований выражение (1.50) примет вид

(р) \2kJiT,,,p {Т,р + 1) т,р +1) + 1

х]2Мф7мЛзРМ7бР -Ы)

"" (пр + 1)+

+ 3klklTp

(бР + 1) + 1

91 J

(1.51)

где Яг = ТЛТиг + Тмг); У!:! = Tmi/ms; Тмб = + П,г+7мз.

Полюсы Тз!, и нули Гоз1, Гозз функции (1.51), т. е. частоты резонансных пиков tOy.gi = l/Tsi, соу.за == l/Tsa и провалов о)оз1 = 17озз, сооза = l/Tosa ЛАХ (со), могут] быть определены при пренебрежении демпфирующими членами в (1.51). При этом

(1.52)

где Лз-=

7 гр 72

i 0э1,0з2 =

Возможность эквивалентирования трехмассовой системы двухмассовой определяется как соотношением параметров механизма, ТАК и настройкой АСУ. При коррекции АСУ только с помощью перестройки регуляторов, когда нижняя частота упругих колебаний соу.31 подавляется за счет инерционности АСУ, чаще всего можно (ограничиться рассмотрением двухмассовой системы.

При использовании специфических видов коррекции, подавляющих частоту Юу.зд и дающих возможность значительно повысить быстродействие АСУ, влияние второй резонансной частоты (Оу.за может оказаться существенным. Коррекция АСУ должна быть выполнена с учетом подавления частоты щ, 33. При этом типовая нормированная ЛАХ lpi разомкнутой системы, настроенной на ОМ или СО, будет аналогична ЛАХна рис. 1.6. Соответствующие обозначения в рассматриваемом случае будут Шу.зр/у.з! = а; (ii/fuy.зГ = ; оооз i/юу.з 1 = Т- Рассуждая аналогично вышеизложенному для системы с упругими связями первого рода, можно получить условие эквивалентирования трехмассовой системы двухмассовой в общем виде:

<

(1.53)

где Ло, 1з2 -запас по амплитуде и коэффициент демпфирования пика ЛАХ ITpi на частоте соу.зг- „

При переходе к первичным параметрам механической системы

условие (1.53) будет

92i(l + 91з + 92з)

<

16Ло:

1(1 + 921 + ) 3(Ло+4зг)

(1.54)

Из анализа выражения (1.54) следует: а) полученное условие гялполняется тем легче, чем меньше (731; б) при одинаковых параметрах ветвей упругой ленты условие зависит только от соотношения инерционных масс системы; в) данное условие в отличие от