

|
|
Главная -> Математическое описание сэп 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 [32] 33 34 Наибольший интерес для СЭП различных промышленных агрегатов представляет оценка чувствительности «в большом» при изменении механической постоянной времени привода Т, характеризующемся коэффициентом у = TJT. Чувствительность «в большом» рассмотрена для двухконтурных систем подчиненного регулирования и инвариантной системы с УКИВ. В качестве оценки чувствительности системы используется усредненная норма вектора чувствительности (5.23). Поскольку при 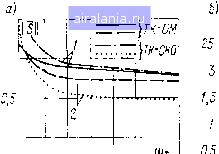 0.25
2 5 is Ю 12 15 20 o,S"" j 2 Г 10 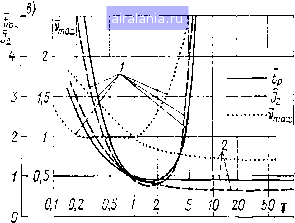 рнс. 5.5. диаграммы усредненной нормы чувствительности и показателей качества СЭП / - исходная СЭП; 2 - инвариантная СЭП вариации механической постоянной времени изменяется частота среза двухконтуриой системы подчиненного регулирования, то ее значение в зависимости от коэффициента у можно определить из рис. 5.5, б (кривая ©с. обозначенная пунктиром). Для инвариантной СЭП с УКИВ частота среза системы в определенном диапазоне значений у практически не изменяется и равна to = l/(2T2i) (см. § 4.6). Графики УНЧ для сравниваемых систем при вариации механической постоянной времени «в большом» приведены на рис. 5.5, откуда можно заключить, что при y>1 инвариантная СЭП характеризуется значительно меньшей чувствительностью, чем система подчиненного регулирования. Однако при 7< 1 чувствительность инвариантной СЭП увеличивается, поэтому при выборе коэффициента = тТд,„ звена .VK1IU т-огьчичим!» [(ipnoi-тироваться на наибольшее значение mcxaiiinu-ckdm iioctmiminii времени привода Т, что обеспечит mniihma./imiyi() чушtunu.-ii, ность системы при ее вариации. Чувствительность «в большом» можно оцепит.......Ill lil II. ной функции чувствительности (ИФЧ) показатели k;i4ii-tii;i Г. которая определяется следующим образом: ИФЧ фактически представляет собой зависимость фупкииоп;!,!.-! качества от некоторого параметра системы q, вариация kuioikjio рассматривается «в большом». На рис. 5.5, в приведены rpa()iiKii интегральных функций чувствительности введенных ранее покач; телей качества при оптимизации токового контура на оптимум но модулю. Показатели качества даны в относительных едипнцп.ч, причем в качестве базовых приняты их значения при 7 - 1. Общие тенденции изменения показателей качества СЭП и УНЧ при вариации механической постоянной времени привода указывают на возможность применения усредненной нормы чувствительности для анализа «глобальной» чувствительности систем управления. 5.5. ИССЛЕДОВАНИЕ ЧУВСТВИТЕЛЬНОСТИ СИСТЕМ ЭЛЕКТРОПРИВОДА С УПРУГИМИ СВЯЗЯМИ при оценке чувствительности двухмассовых СЭП с упругой связью представляет интерес рассмотреть основные разновидности этих систем, а именно: без применения специфических средств коррекции, с примеие1П1ем гибкой отрицательной связи по скорости двигателя и инвариантной. Согласно принципам определения функций чувствительности, запишем обобщенное матричное уравнение системы с упругой связью, составленное в соответствии с рис. 4.13: Ai ip) Xl = f, Ai ip) = -«21 0 0 0 0 0 - «32 0 0 0 «13 «34 1 «72 «73 0 0 0 0 0 1 -«65 0 0 0 «46 «76 (5.24) «27 0 0 0 0 1 f = [uB о о о Ре о Of; fli3 (р; = Wo. z, (Р); 21 (р) = Wp. е(р) Фт. к (Р); «27 (р) = Wk (р) Фх. к (Р); ti32 (Р) - £34 (Р) - W« (р); (Р) = (р) = Wy (р); (р) - Wm (р); «72(p)Wi(p); a;3(p) = W2(p); аб (р) = W3 (р). Рассмотрим передаточные функции СЭП: по управляющему воздействию Ub " Ub(p) detAi(p) ПО возмущающему воздействию рс Рс{р) " detAi(p) (5.25) (5.26) где Л16 (р) и Л56 (р) - соответствующие адъюнкты определителя матрицы Л1 (р). Функции чувствительности определяются следующими соотношениями: detAi(p)" а{Ар) 5 (Р) det Ai(p) Л1б(р) , detA,(pV Лб(Р) (5. 27) (5.28) det At (р) a,dp) где det Ai (p) Л{б (p), Лб (p) находятся из определителя матрицы Ai (р) и соответствующих адъюнкт определителя (р), Л56 (р) путем присвоения элементам матриц, содержащим передаточную функцию W/ (р) нулевых значений. Полагая р = /со в формулах (5.27) и (5.28) и ограничиваясь рассмотрением модуля комплексных функций чувствительности, получим амплитудно-частотные характеристики функций относительной чувствительности передаточных функций S((o). Исследование чувствительности систем подчиненного регулирования с упругой механической передачей. Функции чувствительности для СЭП могут быть получены по соответствующим формулам, если положить Wi (р) = W (р) = W, (р) = Wk (р) = 0. Параметры регулятора скорости выбраны таким образом, чтобы обеспечивались условия устойчивости системы (4.102). На рис. 5.6 приведены АЧХ функций относительной чувствительности передаточных функций системы подчиненного регулирования по управляющему [5 (ш)] и возмущающему [S (©)] воздействиям. При расчетах принято: частота упругих колебаний механической системы Шу = 55 с-, коэффициент соотношения масс д = 0,01. У АЧХ функций относительной 4yni"rmtuvit.....t....... MJii.m ляющему воздействию наблюдаются ;nia4imvii.iii.ii шп i«< mi tm частотах, близких к Шу, практически для всех парамсiр.,ц ( ). .и особенно Гм.д, Гм, Т, Т, Tj, Л„ „.с- J 2 1
0,005 Ofif 0,05 0,1 0,5 1
 0,01 0,05 0,1 0,5 1 5 10
0,0050,01 0,05 0,1 0,5 1 5 10
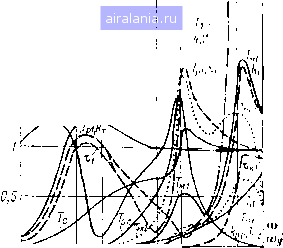
0,01 0,05 0,1 0,5 1 5 10 Рис. 5.6. АЧХ функций относитель- Рис. 5.7. АЧХ функций относительной чувствительности системы с уп- ной чувствительности СЭП с гибкой ругой связью отрицательной обратной связью по скорости двигателя Анализируя АЧХ функций относительной чувствительности по возмущающему воздействию, можно заключить, что СЭП наиболее чувствительна к вариации параметров Tpi, k, ко.с, Т, Tj. Сравнение рассматриваемых АЧХ с аналогичными характеристиками для СЭП с жесткой механической передачей (см. рис. 5.4) указывает на их идентичность (частота среза СЭП с упругой связью ©с = = 0,01(0у). Анализ чувствительности СЭП с гибкой отрицательной обратной связью по скорости двигателя. При расчете ФОЧ для системы с гибкой отрицательной обратной связью по скорости двигателя (ГОС) полагаем в выражении (5.24) передаточные функции Wi (р) = = (р) = 0. У АЧХ функций чувствительности по управляющему воздействию имеются резонансные всплески на двух частотах: один на частоте упругих колебаний, другой на частоте, приблизительно в пять раз превышающей частоту упругих колебаний. Причем резонансные всплески имеются у функций чувствительности по тем же параметрам, что и для системы подчиненного регулирования, но их амплитуда несколько меньше (рис. 5.7). АЧХ функций относительной чувствительности по возмущающему воздействию еще ближе к таковым для СЭП с жесткой механической передачей. а) /
0,01 0,05 0,1 1,5 0,5 1 5 10 COtf
Рис. 5.8. АЧХ функций относительной чувствительности инвариантной системы с упругой связью и диаграммы усредненной нормы чувствительности СЭП / - СЭП подчиненного регулирования; 2 - система электропривода с ГОС; S -инвариантная СЭП 0,21
0,5 1,0 Представляет интерес оценить влияние изменения частоты упругих колебаний на чувствительность СЭП. Графики усредненной нормы чувствительности приведены на рис. 5.8, б. Увеличение чувствительности системы при уменьшении частоты упругих колебаний происходит за счет изменения параметров Т, Tq, kf, k-Q. [23 ]. Оценка чувствительности инвариантных СЭП. Амплитудно-частотные характеристики ФОЧ передаточных функций инвариантной СЭП, имеющей частоту среза (0. 0,5 у. т. е. такую же, как и у СЭП с гибкой связью, приведены на рис. 5.8, а, По сравнению с СЭП с гибкой связью инвариантная система характеризуется значительно меньшей чувствительностью к вариации большинства параметров. Наиболее существенно изменяются АЧХ функций относительной чувствительности по постоянной времени механизма Т, и, следовательно, влияние ее вариации наименьшее для инвариантной СЭП. Из графика УНЧ (рис. 5.8, б) видно, что при и:шстнпм M.uiini.i упругих колебаний инвариантная СЭП имеет наибольтую fi ,i6n./n. ность из сравниваемых систем и характеризуется нанмсньнич! чувствительностью, так как значение УНЧ для нее mhhhm;i,/ii.ho Значительное совпадение АЧХ функций относительно!! чун ствительности передаточных функций по возмущению дли (»И с жесткой и упругой механической передачей позволяет при н.\ оптимизации по возмущающему воздействию использовать математические модели эквивалентных жестких систем [59]. 5.6. СИНТЕЗ ПАРАМЕТРИЧЕСКИ-ИНВАРИАНТНЫХ СИСТЕМ ЭЛЕКТРОПРИВОДА Наряду с анализом чувствительности проектируемых СЭП к вариации параметров несомненный интерес представляет синтез систем электропривода, имеющих ограниченную чувствительность к вариации параметров. Рассмотрим некоторые, наиболее разработанные подходы к синтезу параметрически-инвариантных систем. Синтез систем по критериям параметрической инвариантности и нулевой чувствительности. Условие параметрической инвариантности следует и: условия (5.1) Av [t) = О, которое выполняется при =0. tt= 1, 2, .... 00. (5.29) Условие (5.29) налагает довольно жесткие ограничения на систему, поэтому в большинстве практических случаев выдвигается требование нулевой чувствительности. Оно следует из (5.1) при рассмотрении только первого члена разложения для реализации которого необходимо потребовать, чтобы г;. (0 = 0 или 5.(р)=0. (5.30) Следует отметить, что для линейных стационарных систем понятие нулевой чувствительности эквивалентно понятию параметрической инвариантности. Наиболее полно данный подход рассмотрен в работе [53], где на основе обобщенного топологического анализа получены условия нулевой чувствительности для структур, которые не содержат варьируемых контуров, не касающихся прямых путей. Согласно работе [53], необходимым условием нулевой чувствительности для этих структур является выполнение принципа двухканальности, заключающегося в том, что элемент с нестабильными параметрами должен входить не менее чем в два пути и занимать в них различное положение. Реализация рассматриваемого условия нулевой чувствительности в системах электропривода представляется трудной задачей из-за сложности образования второго пути. Отсутствие разработанных процедур синтеза систем с нулевой чувствительностью к вариации некоторых параметров повышает роль эвристических методов данного исследования. Структурный подход к синтезу систем с учетом требований минимальной чувствительности к вариации параметров объекта управления. Некоторые соображения по выбору структуры системы, обладающей минимальной 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 [32] 33 34 0.0265 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||