чувствительностью, высказаны в работах [34, 42]. При этом исходят из известного факта о том, что для снижения чувствительности предпочтительнее использовать корректирующие обратные связи по сравнению с другими видами корректирующих устройств при формировании заданных передаточных функций системы. Наиболее нестабильный элемент необходимо стремиться охватить наибольшим числом обратных связей [42]. Данную рекомендацию практически сложно выполнить, поскольку, как правило, наиболее нестабильный элемент расположен ближе к выходу системы и поэтому охватывается наименьшим числом обратных связей.

Использование независимых корректирующих устройств, обеспечивающих реализацию желаемых характеристик чувствительности. При синтезе автоматических систем желательно с помощью корректирующих устройств обеспечить наряду с требуемыми передаточными функциями также желаемые функции чувствительности. В работе [42] показано, что при определенном расположении корректирующих устройств эта задача в некоторой степени может быть решена. Построение независимых корректирующих устройств в СЭП зачастую представляет собой сложную и противоречивую задачу-из-за взаимного влияния корректирующих устройств. При использовании данного подхода необходимо выбрать желаемую функцию чувствительности. Если использовать в качестве желаемой нулевую чувствительность, то, очевидно, возникают проблемы, указанные в первом способе.

Построение систем управления с использованием обратных связей по функциям чувствительности. Для уменьшения дополнительного движения, вызванного параметрическими возмущениями, в систему вводятся дополнительные связи по чувствительности, состоящие из модели чувствительности и корректирующих звеньев, обеспечивающих автономную настройку контуров чувствительности.

Как было исследовано в работе [3], использование полной модели чувствительности значительно усложняет СЭП. Целесообразно применять частичные модели чувствительности, которые позволяют снизить чувствительность системы к вариации основных параметров привода.

Синтез оптимальных систем с учетом дополнительного функционала грубости. Синтез оптимальной системы в данной постановке выполняется исходя из условий минимизации основного функционала качества / = = 1{х,У, Т,а) и дополнительного функционала грубости J = J (х, V, Т, а), где X - вектор фазовых координат; V - вектор управления; Т - фиксированный момент времени; а - вектор параметров объекта. Параметры управления V могут обеспечить только минимизацию одного из функционалов при ограничении другого или минимизацию некоторого совместного функционала [42].

Синтез оптимальной грубой системы производится в расширенном фазовом пространстве (т -\- 1) п, фазовые координаты которого определяются в результате интегрирования уравнений:

= F(x, V, а, t), х(о) = Хо;

dt дх да

t =. 1, 2, . . . , m,

где n ~ порядок уравнений системы; т - число варьируемых параметров, Uj- (t) - функция чувствительности.

Для синтеза системы могут быть использованы различные подходы, например метод динамического программирования. Тогда функция управления V (О может быть найдена в виде [42]

V{t)=c{t)x-{ Y,dkit)vik-

Из последней формулы следует, что структура системы дпл/ии! жать устройство для определения функций чувствительности, imiiii. imi,..

о которых используется при управлении. В этом заключается от,;......и ми

ного класса систем от оптимальных систем, синтезируемых без yucr.i i\r., сти. Возможность применения данного подхода для синтеза оптимплмм.м грубых систем электропривода показана в работе В. Л. Анхимюка [3. II" i ное использование данного подхода затруднительно в связи со сложит-и,..> построения модели чувствительности СЭП высокого порядка.

Проектирование параметрически-инвариантных систем электропривода. Особенностью синтеза параметрически-инвариантных систем автоматизированного электропривода широкого класса промышленных установок является необходимость достижения инвариантности, как правило, относительно вариации небольш{)1Ч) числа параметров. Наиболее существенное влияние на свойства системы оказывает изменение механической постоянной времени. Это характерно для ряда установок: моталок, продольно-резательных станков, суперкаландров, накатов и т. д. Поэтому задача синтеза несколько локализируется, так как для многих устройстп имеются адекватные математические модели. В связи с этим сингоч параметрически-инвариантных систем целесообразно производит), по критериям нулевой чувствительности (параметрической пппа-риантности).

Нулевая чувствительность СЭП с жесткой механической lu-pr-дачей к вариации механической постоянной времени 7\, может быть обеспечена, как следует из табл. 5.2, при

А2(Р) = 0,

(г>.;и)

где Дг (р) = 1 Li(p) - для системы подчиненного регулирования; До (р) = 1 f L, ip) -- /.4 (р) - для инвариаптиои системы; Li (р), L4 (р) определяются из формулы (5.18). Отсюда следует, что в системах подчиисппого регулирования нулевую чувствительность реализовать нельзя. В СЭП с УКИВ условия параметрическо!) инвариантности выполняются при выборе параметров компенсирующего устройства следующим образом:

:. У (Р) = Ц-ТТ = « Thp + аТ,р + 1.

(5.32)

Таким образом, условия инвариантности ло возмущению и (4.40) и параметрической инвариантности по (5.32) полностью совпадают.

В силу обстоятельств, указанных в § 4.4, при использовании пропорциональных и пропорционально-дифференциальных комиси сирующих устройств можно реализовать только условия ограни ченной чувствительности к вариации механической постояmmu времени. В частотной интерпретации это означает дефоркь-тш" АЧХ функции относительной чувствительности в области vywu-* t венных частот системы и ее перемещение в область <.....

высоких частот (ср. АЧХ функции относительной чувствительности по параметру 7", показанные на рис. 5.2 и 5.4).

Обобщая результаты анализа чувствительности и синтеза СЭП с косвенным измерением возмущения, сформулируем следующий подход к синтезу с ограниченной чувствительностью к вариации некоторых параметров: для обеспечения ограниченной чувствительности системы к вариации некоторого параметра необходимо включить звено, имеющее нестабильный параметр, в устройство косвенного измерения возмущения, параметры которого определяются из условия нулевой чувствительности системы к вариации рассматриваемого параметра. Если нестабильный параметр при-

- -(Л

-/ Ун Wn

%2 %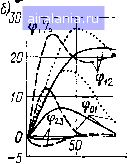

/

ц.. Рис. 5.9. Сигнальный граф многосвязной

U, АСРН непрерывно - по- f точного агрегата и переходные процессы

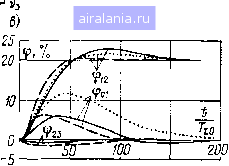надлежит звену, на входе которого действует возмущение, компенсируемое УКИВ, то система приобретает свойство двукратной частичной инвариантности по отношению к вариациям внешнего возмущения и данного параметра.

Синтез параметрически-инвариантной системы регулирования натяжения обрабатываемого материала в непрерывно-поточном агрегате. Рассмотрим синтез компенсирующих устройств для контура регулирования натяжения материала многосвязной системы управления непрерывно-поточным агрегатом (НПА), сигнальный граф которой приведен на рис. 5.9, а. Сигнальный граф автоматической системы регулирования натяжения обрабатываемого материала (АСРН) составлен на основе известной математической модели [59 ].

В контур регулирования натяжения, состоящий из датчика натяжения с передаточной функцией (р), регулятора натяжения

с передаточной функцией н (р) и системы стабилизации скорости электропривода, входит также звено с передаточной функцией Wvi2 ip) i,rJ(TbviP + 1), параметры которого зависят от технологических 1! скоростных режимов работы НПА [59]:

lioVl ---Т--- 612--ГГ-.

где Vci, Vciлинейные скорости соответственно первой и второй секций ИПА; Е,.,, S - модуль упругости и площадь поперечного сечения обрабатываемого материала; Fci2 - статическое натяжение материа.ла; /,,.j - длина межсекционного промежутка.

Из-за наличия и контуре регулирования натяжения обрабатываемого материала звена с передаточной функцией Wiz (р), в которую входят переменные параметры, зачастую не удается реализовать оптимальные настройки регулятора натяжения.

Для компенсации влияния на АСРН переменных параметров будем использовать сформулированный выше принцип синтеза систем с ограниченной чувствительностью. Косвенное измерение нестабильных параметров, входящих в передаточную функцию Wvi2 (р), осуществляется посредством образования дополнительных связей по разности скоростей смежных секций непрерывно-поточного агрегата и сигнала, снимаемого с датчика натяжения (дополнительные связи показаны на рис. 5.9, а штриховой линией).

Параметры передаточных функций дополнительных связей Wl (р) и (р) выбираются из условия выделения параметрических возмущений следующим образом:

Wi{p)-W,{p)W„{p) W,n{p)0

Wiip)=

2 ip).

(5.33)

где kn, Гд. н - соответственно коэффициент передачи и постоянная времени датчика натяжения. При этом целесообразно выбрать передаточную функцию W (р) = 1/(нг12)- Тогда из (5.33) получим

Wiipy

(5.34)

где Tl - Т

д. н

Передаточная функция ttj. (р) определяется из условия нулевой чувствительности. Для этого найдем функцию относительной чувствительности передаточной функции системы по натяжению обрабатываемого материала к вариации параметров kyi,, и Гхз, используя матричный способ расчета ФОЧ.

Учитывая, что натяжение материала практически регулируется между двумя секциями, при составлении матричного уравнения системы ограничимся рассмотрением только этих секций.

Матричное уравнение многосвязной системы с контуром натяжения можно представить следующим образом:

A(p)x==B(p)f,

(5.35)

А(р) =

О О О О

«42

В(Р) =

о о о

о о о о о о

«13

«63 «73

о о о о о

«24

-«64

«25

«27

- «74

о о о о

о о 1 о о

о о о

о о о

«36 «46

«56

«76

о о о о

о о о о 1

X==[li 12 Vl V2 Up.H ф12 ;

t = [lJEi Ub2 Pel VC2 H3?\ «]з(Р) = Wp.cl{p)tJDr.Kl(P); «24 (P) --«25 (P) = «27(P) = р.е2(р)Фт.кз(Р); «3l(P)-W«i(p); «36(Р)-1Д1{Р);

«42 (p) = д2 (p); «46 (p) = ф12д2 (p);

«56 (P) = Wp. H (P) r H (P); «63 (P) = (P) X

X [l - Wm (P) i]; «64 (P) = W„i2 (p);

«73(p) = «74(p)=W,(p)ri(p); «76 (P) = (p) r2 (p) r „ (p); bn (p) =

=Wp. ,1 (p) Фх. Kl (p); 22 (P) Wp. e2 (p) Фт. K2 (P);

£зз(p) = Wдl(p); £44 (P)=W«2(P);

fc55(p)-=Wp.H(p).

Передаточная функция по натяжению бумажного полотна может быть записана так:

W 12 (р) = 12 (Р) „ ,в(Р) Лг.в(р)

Фн.з(Р)

det А(р)

Согласно выражению (5.16), функция относительной чувствительности передаточной функции системы по натяжению 1ф1г (р) определяется выражением

S%, („ч detA(p)- [Ь,,{р)Л,Лр)] -2 detA(p) Ь,,{р)Аь,{р)

где det А (р), [Ь (р) А,в {р)У определяются из соответствующих матриц при коэффициентах аз (р) = «64 (р) ~ О-При этом получаем

SP (t)) - П - "i3 (р) Дзг (р)] 1 - а24(р)Д42(Р)[1 - а74(Р)]} /5354 «2 detA(p) \ f

Положив Sw (р) = О и учитывая, что [1 - «13 (р)«з1 (р) ] О и det А (р) 7 О или det А (р) 00, из формулы (5.36) имеем

1 -024 (Р) «42 (Р) [1 - «74 (Р)] = 0.

Из этого выражения с учетом (5.35) можно определить передаточную функцию Wk (р):

.у. (8ri,p + 8Г,,р + JT ,,р + 1) (Г,р + 1

(5.37)

Как видно из формулы (5.37), реализовать нулевую чувствительность в системе нельзя, можно достигнуть только ограниченной чувствительности к вариации „12 и тх2> применив, например, пропорциональное компенсирующее устройство с передаточной функцией Wk (р) = 1.

Переходные процессы по натяжению, рассчитанные на ЦВМ для высокопроизводительной бумагоделательной машины, представлены для исходной системы с контуром регулирования натяжения (б) и для инвариантной АСРН (в) на рис. 5.9 при одинаковых значениях механических постоянных времени секций.

Переходные процессы, определенные на верхнем уровне скорости (Ув) при номинальном значении коэффициента к (иком)» для сравниваемых АСРН практически совпадают (кривые, обозначенные сплошными линиями). Однако при переходе на нижний уровень скорости (1/„ 0,2) в исходной АСРН наблюдается значительное увеличение колебательности переходных процессов по натяжению, а в инвариантной АСР переходные процессы почти не изменяются (штриховые кривые). Высокую эффективность синтезированной АСРН подтверждают также переходные процессы, снятые на верхнем уровне скорости БМ при увеличении коэффициентов k.i в три раза (пунктирные кривые).