формулы (1.41) для системы с упругими связями первого рода зависит от скорости привода (поскольку значение пропорционально скорости ленты); поэтому проверка его выполнения должна быть проведена на нижней скорости ЭП.

Обратимся к рассмотрению трехмассовой системы с разомкнутыми упругими связями второго рода при наличии одного приводного вала. Проведя соответствующий анализ динамики АСУ при условиях, оговоренных в предгадущем случае, можно получить искомое условие эквивалентирования трехмассовой системы двухмассовой в общем виде

(1.55)

где Aq, Io2-запас по амплитуде и коэффициент демпфирования пика ЛАХ Wpi на большей частоте упругих колебаний Шуог;

При записи условия (1.55) через первичные параметры механической системы получим

(2-i Qi,-\q,3y (Ло + 4о2) *

Структура данного выражения аналогична формуле (1.54), Следовательно, выводы об особенностях эквивалентирования, сделанные выше для систем с замкнутыми упругими связями второго рода, остаются Б силе для систем с разомкнутыми связями.

В заключение следует отметить, что на базе полученных выше НСС типовых узлов систем электропривода могут быть построены адекватные нормированные структуры электромеханических объектов управления промышленных агрегатов с упругими связями первого и второго рода. НСС являются удобным математическим описанием многодвигательных СЭП, физически наглядны и пригодны для применения различных инженерных методов исследования динамики - как ручных, так и машинных. Параметры НСС могут быть сравнительно легко определены расчетным или экспериментальным путем (см. § 1.4), что повышает эффективность использования НСС в ходе исследования и наладки промышленных ЭП.

1.3. СТРУКТУРНО-ТОПОЛОГИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ СИСТЕМ ЭЛЕКТРОПРИВОДА

При исследовании дина.мики систем электропривода могут быть применены различные расчетно-аналитические и машинные методы. К расчетно-аналитическим можно отнести классический, операторный и частотный методы, различные численно-графические и графические методы, а к машинным - моделирование на аналоговых и цифровых вычислительных машинах (АВМ и ЦВМ). В зависимости от характера решаемой задачи возможно при 28

liiliiHHe одного из указанных методов на конкретном этапе исследования щщы сочетание различных методов, дополняющих Друг друга и позволяющих М1Иболее полно и с наименьшими затратами времени провести анализ или IMHTis системы.

Общий подход к исследованию динамики СЭП может быть следующим. Hi основе разработанной функциональной схемы СЗП составляются исходим* линейные и нелинейные дифференциальные уравнения отдельных §ньев и узлов системы (силовая электрическая и механическая части СЭП,

вобразователи, датчики и т. д.). Для исключения из уравнений ряда коэффициентов и получения общности проводимых исследований целесооб-IHO использовать относительные единицы. С помощью составленной си-мы уравнений компонуется нормированная структурная схема (НСС) П, являющаяся математической моделью реальной системы. НСС наглядно §Тражает вид динамических звеньев и характер связей между ними и в об-

а1М случае получается нелинейной. Для предварительного исследования 1П, выявления «веса» отдельных параметров и связей и разработки исходных рекомендаций по оптимизации контуров целесообразно провести линеа-рИнцию нелинейной системы в характерных режимах ее работы, если.ко-Мчио, линеаризация допустима. При исследовании линеаризованной СЭП применяются линейные методы расчета динамики, в частности операторный, 1стотный и др. Применение частотного метода дает возможность наиболее Просто осуществить синтез СЭП и в первом приближении оценить характер Й1р€Ходных процессов в системе.

После такой предварительной оценки динамических свойств СЭП целесообразно перейти к более полному анализу нелинейной системы во всей §010купности параметров и связей. Такая задача может быть успешно ре-ШШа с помощью моделирования на АВМ и ЦВМ, поскольку в ходе исследо-йвния линеаризованной СЭП нередко удается уточнить программу работы N1 вычислительных машинах. Применение машинных методов ускоряет получение результатов, в особенности если исследуется несколько различных цриантов построения и оптимизации системы. На данном этапе могут быть § успехом применены и расчетно-аналитические методы исследования нелинейных систем, в частности метод гармонического баланса. Такое комплекс-Иое исследование СЭП позволяет скорректировать рекомендации по оптими-11ЦНИ, сформулированные выше для линеаризованной системы, а в ряде слу-Ч1ен и разработать новые способы коррекции нелинейной СЭП. Окончательное ьуждение о качестве динамики синтезированной СЭП можно сделать после Прпиедения соответствующих экспериментальных исследований.

Изложенная последовательность исследования СЭП с помощью сочетании различных методов позволяет наиболее полно изучить особенности систем и принять рациональные решения по их построению. С этих позиций ниже рассматриваются возможности некоторых современных инженерных М#т<1Дов расчета динамики промышленных систем электропривода и автома-

fHKH.

Метод структурных преобразований СЭП. Составление НСС является итггравным моментом при исследовании СЭП структурными методами (ча-итотмые, графические, моделирование на АВМ и ЦВМ). Правила преобра-шнпиия линейных структур достаточно широко освещены в литературе II, 50]. Ряд приемов преобразования нелинейных НСС изложен также W работе [13]. Все эти способы направлены в основном на объединение последовательно и параллельно соединенных звеньев, свертку контуров и устранение перекрещивающихся связей, что в результате дает возможность Ийиболее просто осуществить анализ и синтез СЭП расчетно-аналитическими, тмхс всего частотными, методами. При исследовании динамики машинными Методами, в частности при моделировании на АВМ, иногда возникает задача fenoro преобразования структурной схемы СЭП, чтобы в ней отсутствовали дифференцирующие звенья, труднореализуемые в схемах набора на АВМ. При подобных преобразованиях необходимо пользоваться специальными приемами, заимствованными из теории направленных графов и требующими щшмсиения инверсии (изменения направления) пути или контура структур-

1.1» tftiww 113]. при зтом передаточные функции ряда звеньев сэп из-тнлтся на обратные, что позволяет заменить дифференцирующие звенья НА интегрирующие и тем самым подготовить структурную схему системы к исследованию на авм,

при исследовании сложных многоконтурных сэп структурно-топологическими методами преобразование исходной структурной схемы с целью получения необходимых передаточных функций становится весьма громоздким и требует больших затрат времени. в этих условиях более эффективным является применение из1зестного правила мэзоиа, сформулированного в теории илпраклоппых (сигнальных) графов [48]. учитывая аналогию структур-1п,1х схем п 1-рг1фоп, можно распространить правило мэзона на структурные гхомы (>эп. в соответствии с этим правилом передаточная функция между лиумя любыми переменными структурной схемы может быть определена по

W ([Л „ (Р) 1Рпрс(Р)(1--Гки-(р)+к2((р)-1гкзг(Р)+- •] хт(р) 1 1-2 \к1(р) + 2Гк2(р)--2«?,з(р)4. . . .

(1.57)

гдг wjjpf (/?) - сумма передаточных функций всех прямых путей от -Im (/) ло ir); 2 Wkji (р) - сумма передаточных функций всех контуров, пе клслющихся i-rn прямого пути; ZW.i (р) - сумма произведений переда-TOitibix функции иссх пар контуров, не касающихся i-ro пути и друг друга; 2 Wks (р) -сумма произведений передаточных функций всех троек контуров, не касающихся t-ro пути и друг друга и т. д.; s ifm (р) - сумма передаточных функций всех контуров асу; s 1к2 (р) - сумма произведений передаточных функций не касающихся друг друга пар контуров; 2 DFks (р) -• сумма произведений передаточных функций не касающихся друг друга троек контуров и т. д.

при этом передаточные фуикцяи контуров берутся с их знаками, т. е. со знаком плюс при положительной обратной связи (ос) и со знаком минус при отрицательной ос. заметим также, что некасающимся контуром считается контур, не имеющий ни одной общей координаты (переменной) с другим контуром или путем.

длительность математических преобразований передаточных функций, полученных по правилу мэзона, зависит в общем случае от сложности исходной структурной схемы сэп. применение машинных методов расчета сложных передаточных функций является при ьтомвесьма эффективным.

частотный метод исследования динамики СЭП. несмотря на широкое развитие и применение машинных методов исследования сэп, интерес к частотным методам пе уменьшился, что обусловлено как универсальностью частотного метода и удобством синтеза систем, так и методологией самого процесса исследования сэп. в основе различных структурно-топологических методов лежит единое математическое описание, в общемслучае система нелинейных дифференциальных уравнений, трансформирующихся в дальнейшем применительно к конкретным методам. при этом последние оказываются взаимосвязанными и дополняющими друг друга на каждом этапе исследования.

применение частотного метода целесообразно на начальном этапе исследования линеаризованной системы, поскольку с"его помощью наиболее удобно «почувствовать» специфику работы сэп, выявить существенные параметры и связи, исследовать влияние «малых» параметров, провести синтез регуляторов и корректирующих обратных связей и дать предварительную оценку динамических свойств системы. вместе с тем частотные методы могут быть с успехом использованы и иа более позднихэтапах исследования сэп, например в сочетании смашиппыми методами илив ходе экспериментальных исследований.

на практике получили наибольшее распространение логарифмические частотные характеристики (лчх), обладающие известными достоинствами. при этом используются лчх как разомкнутой, так и замкнутой системы. 30

информацию о переходных процессах содержат как те, так и другие харак-ftpHCTHKH. связь переходных процессов в замкнутой системе с лчх разомк-Йу?ой сэп описана в работе [24], а зависимость между переходными и ча-1Т0ТНЫМи характеристиками замкнутой системы - в работе [14]. последний (Ц§ТОд весьма полезен на стадии пусконаладочных работ и идентификации сп. при качественной оценке переходного процесса по управлению или »01мущению следует руководствоваться общим правилом, что начальная «йдия переходного процесса определяется высокочастотной частью соот-мтствующей лчх, а конец процесса - низкочастотной частью характери-цтнки. для выявления параметров переходной функции следует провести аппроксимацию логарифмической амплитудной характеристики (лах) замкнутой системы отрезками прямых с типовыми наклонами.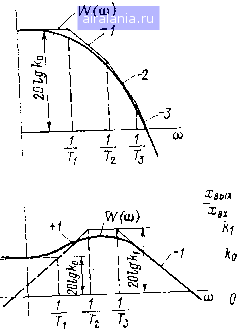

рис. i.9. логарифмические частотные и переходные характеристики системы

на рис. 1.9 приведены примеры связи лах и переходных процессов fi (эп. нетрудно видеть, что форма переходного процесса напоминает форму Амплитудной характеристики, повернутой относительно оси ординат на 1ж)". если лах замкнутой системы во всем диапазоне существенных частот «пляется монотонной и не имеет резонансных подъемов над уровнем 20 ig k(j, 10 переходная функция системы также монотонна. если же в амплитудной характеристике имеется резонансный всплекс на какой-либо частоте, то перерегулирование переходной функции определяется коэффициентом пере-дпчн сэп на этой частоте. прохождение лах в зоне низких частот с положи-гсльпым наклоном обусловливает стремление переходной функции к нулю прн / оо (см. штриховые характеристики на рнс, 1.9). на основании аналогичных рассуждений дается оценка динамики сэп и при ином виде лах i.jMKiiyToft системы. разумеется, такая оценка является приближенной, од-илко ее использование помогает качественно оценить динамику системы, uc прибегая к расчету переходных процессов.

частотные методы применяются такйе довольно широко для исследова-fiiMi периодических режимов (автоколебаний) и переходных процессов в не-ионных системах. при исследовании автоколебаний в сложных сэп с одним нлн несколькими нелинейными звеньями (нз) используется метод гар-моилчоского баланса, основанный на гармонической линеаризации характе-

ристик нз. При этом более целесообразным является применение логарифмических характеристик, поскольку они могут быть представлены в виде шаблонов [17, 51]. Практика использования метода шаблонов для исследования автоколебаний в унифицированных СЭП с упругими связями показала его эффективность {7, 60].

Моделирование СЭП на АВМ, Моделирование систем электропривода на АВМ получило в настоящее время широкое распространение в исследовательской и проектной практике. Использование АВМ при исследовании динамики позволяет более глубоко изучить характер переходных процессов во всех звеньях СЭП, с наименьнгими затратами времени проанализировать поведение системы при различных нид-чх управляющих и возмущающих воздействий, а также при различном сочотапии параметров объекта регулирования и в конечном итоге num.icirn. эффективность проектирования и наладки промышленных СЭП.

Иг tl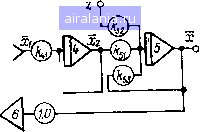

Рис. 1.10. Структурная и наборная схемы типового контура

Преимуществами моделирования на АВМ перед ручными, а иногда и экспериментальными методами являются; эффективность исследования многоконтурных нелинейных СЭП с разветвленной силовой электрической частью и многомассопыми механическими системами с упругими связями; возможность быстрой перестройки модели при изучении влияния отдельных параметров, внешних и внутренних возмущений и различных вариантов структуры СЭП; возможность исследования предельных нагрузок и аварийных режимов работы СЭП.

В практике использования АВМ получили распространение методы машинных уравнений и структурного моделирования.

Следует отметить, что, хотя сам процесс составления машинных уравнений довольно прост, этот метод имеет ряд недостатков, особенно ярко проявляющихся при моделировании замкнутых систем электропривода: большое число однообразных вычислительных операций; невозможность использования при компоновке схемы набора на АВМ результатов предварительной работы по составлению структурной динамической схемы СЭП; получение переходного процесса, как правило, по одной переменной и в связи с этим отсутствие информации о других регулируемых координатах системы; труд-кости при проверке расчета коэффициентов схемы набора и отыскании оши

бок в работе модели.

В связи с этим наибольшее распространение при исследовании СЭП по лучил метод структурного моделирования, сущность которого состоит в том, что схема набора на АВМ компонуется в полном соответствии со структур-

noil схемой реальной системы. При этом структурная схема системы пред-1т;п1ляется состоящей из типовых динамических звеньев, Тогда расчет коэффициентов передачи по входам усилителей АВМ с учетом принятых масштабов переменных и времени осуществляется путем: а) умножения коэффи-iiucMiTOB передачи звеньев структурной схемы на отношение масштабов переменных этих звеньев (выхода ко входу); б) умножения постоянных времени звеньев на масштаб времени. Эти правила очевидны из самого хода со-cтiвлeния машинных уравнений звеньев СЭП.

Структурный метод проиллюстрируем на примере моделирования типового контура системы подчиненного регулирования, структурная схема которого приведена на рис. ЫО. Контур содержит ПИ-регулятор с динамическим коэффициентом передачи р и постоянной времени т и объект регулирования, состоящий из двух апериодических звеньев с коэффициентами передачи и 2 и постоянными времени То и Т. из которых является большой, а - малой. На контур действуют управление лу и возмущение г, выходной координатой является х.

Для компоновки схемы набора ПИ-регулятор а следует его передаточную функцию представить в виде суммы пропорциональной и интегральной частей:

С учетом этого на том же рисунке изображена схема набора рассматриваемого контура на АВМ, скомпонованная по принципу структурного моделирования. Нетрудно видеть, что каждому звену структурной схемы соответствует СБОЙ моделирующий усилитель или группа усилителей, а общая структура контура и схемы набора совпадают. Для получения на АВМ отрицательной обратной связи в схему набора введен инвертирующий усилитель 6. В соответствии с вышеизложенным правилом коэффициенты схемы набора рассчитываются по формулам:

; й,2 = -&;

xmtmxy

--; = .; =--

- -;-> «52 - -;-, «53 - ~-

Tomttrixi TftTz Tmt

где Шху, nixi, /Пх2, Щ - масштабы переменных; /п - масштаб времени.

Основные трудности при расчете коэффициентов модели тиристорных ЭП вызывает наличие в последних динамических звеньев с резко различающимися коэффициентами передачи (от 10"" до 10 и более) и постоянными времени (от 10- с до нескольких секунд), что приводит к большому разбросу коэффициентов схемы набора. Если окажется, что некоторые коэффициенты схемы набора выходят за пределы возможных значений для данной АВМ, то следует изменитьсоответствующие масштабы переменных. В линейной системе допустимо также перераспределение коэффициентов передачи отдельных усилителей по прямым путям или замкнутым контурам. В ке-линейиоА СЭП перераспределение коэффициентов передачи между звеньями, разделенными нелинейностью, сопряжено с соответствующим масштабированием последней.

Большое значение имеет также выбор .масштаба времени т/. Практика моделирования унифицированных тиристорных СЭП показала, что наиболее ул.ччным следует считать от/ = 5 -f- 20, так как при этом получаются приемле-Mt.it коэффициенты на входах усилителей, моделирующих звенья с малыми