

|
|
Главная -> Математическое описание сэп 0 1 2 3 4 [5] 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 постоянными времени, и удобен визуальный просмотр переходных процессов на экране осциллографа. После расчета коэффициентов усилителей по входам следует убедиться в правильности вычислений, что позволяет обеспечить соответствие наборной схемы реальной системе. Такая проверка при структурном методе моделирования базируется на сравнении статических характеристик .модели и системы и осуществляется по прямым путям и контурам схем. Коэффициент передачи i-ro прямогг) пути структурной схемы npicx ~- vwy.iiX}ixi- (1.58) Соответственно коэффициент переламп того же пути в модели kvplM Xauxclxixi (1-59) или с учетом масштабо-а переменных xuxi ~ выхсвых; -Bxt --"axj bxt a.60) При наличии Гнов"соот\етт?у\о;иГ~ " интегральной частям a-l формула (1.60) может быть записана в виде Т р У (1.61) где п - число «чистых» антеграторои. Для замкнутых контуров, т. е. таких прямых путей, у которых muxi - = maxi, формула (LG1) примет вид Kiu-KlJmb (1.62) Таким образом, в общем случае проверка производится по формулам (1.61) и (1.62), хотя в большинстве случаев достаточно проверки по формуле (1.62). Применительно к рассматриваемому контуру (рис. 1,10) можно записать I. 1 п 51 1,0, причем к.м= к. сх- После набора электронной модели необходимо убедиться в правильности ее работы. При структурном методе контроль работы модели упрощается, так как в модели, отражающей структуру реальной системы, все напряжения соответствуют реальным переменным и по характеру изменения этих напряжений в статике и динамике можно судить о достоверности модели. Такая проверка может быть проведена в несколько этапов: 1. Контроль работы узлов схемы набора (механическая и силовая электрическая части привода, регуляторы, отдельные контуры системы и т. д.). При этом снимаются переходные характеристики узлов схемы и производится их анализ на соответствие предварительным расчетам или априорным физическим соображениям. 2. Контроль работы модели в статике по главному прямому пути (от входа к выходу модели) или по дополнительным путям. При этом на вход модели (или данного пути) подается сигнал jCbx и контролируется сигнал дгвых. а затем по формуле (1.59) определяется пр.м- Достоверность модели оценивается по выполнению условия (1.60). ;. Проверка соответствия переходных процессов по управлению и воз-мущмиию U модели частотным характеристикам реальной системы, полученным расчетным или экспериментальным путем. 4. Проверка соответствия частотных характеристик модели и системы, m ущсствляемая путем снятия частотных характеристик с помощью специа-,»мми ипипиюй инфранизкочастотной аппаратуры [15]. 1ри исследовании на АВМ многоконтурных нелинейных АСУ целесо-нбрйзпо вначале рассмотреть динамику линеаризованной системы, что дает 1иам()Жиость определить существенные параметры и связи объекта регули-potseiiHH и предварительные настройки регуляторов. После подобных иссле-дптший можно перейти к моделированию СЭП с учетом нелинейностей и всей 1чшокупиости параметров. При структурном методе моделирования введение нелинейных звеньев в тхему набора осуществляется в соответствии с их по-Л(»й<ением в исходной структурной схеме системы. Несмотря на эффективность моделирования при исследовании СЭП, оно имеет и слабые стороны, связанные как с методикой набора решаемых задач II погрешностью решения на АВМ дифференциальных уравнений, так и с трудностями синтеза системы. При исследовании нелинейных СЭП с резко рияличающимися парадетрами динамических звеньев нередко возникают (рудности реализации коэффициентов схемы набора, что заставляет применить дополнительные моделирующие усилители или идти на упрощение структуры модели. Если на АВМ отсутствует автоматическая установка коэффициентов и нелинейных зависимостей, то сравнительно много времени ребуется на подготовку схемы набора. Погрешность решения линейных задач на АВМ может достигать 5%, » нелинейных - 10% вследствие конечного значения коэффициентов уси-.неиия операционных усилителей, погрешности проводимости входной цепи и цепи ооратной связи, дрейфа нуля усилителей и неточности установки передаточных коэффициентов и функциональных зависимостей. Указанные погрешности снижают точность проводимых исследований и затрудняют йнализ малых параметров, которыми в основном и определяются переходные процессы в оптимизированных СЭП. Существенным недостатком моделирования на АВМ, как и всех машинных методов, является сложность синтеза структуры и параметров, регуляторов. Хотя в настоящее время и имеются примеры синтеза систем электропривода машинными методами [30], эту проблему еще нельзя считать окон-чнтельно решенной. Анализируя возможности моделирования на АВМ, его достоинства и недостатки, можно определить место данного метода в общей методологии исследования динамики электромеханических систем. Моделирование на АВМ целесообразно применять после предварительного исследования систем рас-четно-аналитическими методами, например методом логарифмических частотных характеристик. Такое исследование позволяет сравнительно просто оценить влияние малых параметров, определить существенные связи в системе и в первом приближении синтезировать настройки регуляторов. Далее проводится исследование системы на АВМ, сначала линеаризованной (в режиме малых отклонений переменных), а затем нелинейной («в большом») при различном характере управляющих и возмущающих воздействий, изменения структуры и параметров объекта и т. п. Для уточнения расчетов на АВМ, а также для более детального изучения особенностей работы системы целесообразно применять ЦВМ, обладающие большими возможностями алгоритмизации процесса исследования и более развитым математическим обеспечением. 1.4. ИССЛЕДОВАНИЕ ДИНАМИКИ СИСТЕМ ЭЛЕКТРОПРИВОДА НА ЦВМ Цифровые вычислительные машины в настоящее время находят все большее применение при исследовании и разработке систем электропривода различных промышленных установок. среди задач, для решения которых используется ЦВМ на стадии первичного проектирования СЭП, значительный удельный вес составляют задачи моделирования, представляющие собой основу машинных методов анализа и синтеза систем управления- Цифровое моделирование является разновидностью математического моделирования - современного эффективного метода исследования сложных систем упрспзлспия. Сравнительная оценка способон моделирования указывает на определенные преимущества цифрового моделиринаипя перед аналоговым: повышается точность исследования линейных и нелинейных, стационарных и нестационарных СЭП, причем реализация пелииейных зависимостей или переменных параметров значительно упрощается и может быть выполнена более точно, чем на АВМ; исключается необходимость масштабирования переменных и выполнения коммутационных соединеиии при моделировании; требуется мало времени на смену задачи, поскольку программы моделирования хранятся на перфолентах, перфокартах, магнитных лентах и других носителях информации; представляется возможность простого выполнения операций дифференцирования и интегрирования 1ю невременньш параметрам, В качестве недостатков модел1ф01>а11н я на ЦВМ следует отметить невысокую наглядность выводимо!! 1Пп1)ормации, если ЦВМ не имеет дисплея; большее время расчета по программе моделирования, чем на АВМ. Однако, если учесть сомремеипые тенденции развития средств цифровой вычислительной техники и отмеченные riUJiie факторы, цифровое моделирование в ряде случаев оказывается эффективнее аналогового. При моделировании на ЦВМ все операции выполняются в цифровой форме с использованием методов численного анализа, в том числе операции интегрирования и дифференцирования. Рассмотрим кратко основные методы численного интегрирования обыкновенных дифференциальных уравнений. Методы численного интегрировання обыкновенных дифференциальных уравнений. Как правило, решение дифференциальных уравнений, описывающих динамику СЭП, не может быть получено аналитическими методами. В этом случае целесообразно использовать численные методы решения дифференциальных уравнений. Предположим, необходимо найти решение дифференциального уравнения y=f{x,y) (1.63) при условии, что Xq А X; у {хц) = уд. Будем считать, что уравнение (1.63) имеет единственное решение и необходимо определить приближенное решение данного уравнения в некоторых точках X(i<.Xi<.X2<. .<.Хп- X. Разложим решение у {х) уравнения (1.63) в ряд Тейлора в окрестности некоторой точки xi: У{Х)=У (Xi) + il у (Xi) + -- У" (Xi) + . . . (1.64) Дифференцируя уравнение (1.63) необходимое число раз, можно найти любую производную"г/ (л;!-), и, следовательно, вычислить (1.64) с любой степенью точности. Дифференцирование переменных обычно сопряжено с определенными трудностями, поэтому разработаны методы численного интегрирования дифференциальных уравнений, позволяющие находить значения переменной у на следующем шаге вычисления yi+i, используя информацию, полученную на предыдущем шаге (ус, xi), и не требующие вычисления производных от fix, у). Причем эти методы позволяют обеспечить точ. Ность решения вплоть до члена / (х) [у (х)] разложения в ряд Тейлора, где k определяет порядок метода. Метод Эйлера (метод первого порока). Если ограничиться двумя членами ряда Тейлора (1.64), то получим формулу Эйлера yi+i = yi + hf {Xi, yi), (1.65) I 1Ц - известное значение переменной у; t/j+i-вычисленное новое зна-чриие переменной у; h - Xj-t-i-xi - шаг интегрирования; xi - известное чкнкмше аргумента, совершенствованный метод Эйлера-Коша (метод второго порядка). Чничеиие трех первых членов ряда (1.64) с точностью до малых более высокою порядка можно получить по формуле Коши [27] yt+i = i + -(i + 2). (1.66) г W ki = hf {Xi, yi); = hf {xi+ъ Ус + i)- Метод Рунге-Кутта (метод четвертого порядка). В этом случае рИ1(матриваются пять первых членов ряда (1.64), которые с точностью до м/1,1ых более высокого порядка можно вычислить по формуле [27] У1+ i = yi+{kx + 2k, -Ь 2Аз + ki), о (1.67) i и> = hf {xi, у()] k2 hf {Xi + h/2, yi + Ai/2); k = hf {xi + h/2, yi + i k,/2); = hf {Xi -\-h, yi+ k,). Следует заметить, что указанные методы численного интегрирования км ко распространяются на системы дифференциальных уравнений. По-iptHHiocTb вычисления для рассмотренных численных методов складывается ill методической составляющей, связанной с отбрасыванием остатка ряда hluiopa и приближенно оцениваемой величиной, пропорциональной h, II (оставляющей погрешности, накапливающейся от шага к шагу из-за того, чю при вычислении следующего значения переменной yi+-i используется И1(1чеиие yt, определенное на предыдущем шаге интегрирования с некоторой (мпрешностью. Из перечисленных методов наиболее точным является метод Рунге- К.угта, поэтому в стандартное математическое обеспечение ЦВМ входят М()Д11)0граммы численного интегрирования систем обыкновенных дифферен-цпильных уравнений с постоянным шагом и автоматическим выбором шага ипгогрирования. Но с увеличением порядка метода при одинаковом шаге ипгсгрирования практически пропорционально возрастают затраты машинного времени на решение дифференциального уравнения. В зависимости от црлей моделирования и предъявляемых требований следует идти на ком-иИ)мисс и выбирать между точностью и временем решения. Для инженерных исследований динамики СЭП зачастую по точности имолне приемлемы методы первого и второго порядка. Окончательный выбор численного метода решения и шага интегрирования производится экс-е)нментально на основании сравнительной оценки затрат машинного вре-М1Ч1Н и полученной точности решения при моделировании СЭП. Цифровое структурное моделирование систем электропривода. Если \ честь широкое распространение в инженерной практике структурно-топологических методов исследования СЭП, использование стандартных подпрограмм численного интегрирования систем дифференциальных уравнений циЛует значительной подготовительной работы по переходу от разработанной структурной модели системы к переменным состояния. С целью повышения эффективности применения ЦВМ для исследования СЭП целесооб-р.пио разработать специальные методы цифрового структурного моделиро-плпия, сводящие подготовительную работу по постановке задачи на ЦВМ до минимума и позволяющие наиболее полно использовать информацию, полученную на первичной стадии исследования. Метод структурного моделирования, наиболее полно разработанный 1.1 II ЛВМ, нельзя считать оптимальным при цифровом моделировании, поскольку требует существенных изменений программы моделирования при иее.иедовании различных СЭП. Для ЦВМ целесообразен другой подход, основанный на использовании единой модели универсального звена, являющейся ядром программы цифрового структурного моделирования [38, 44]. Структурная схема обобщенного алгоритма моделирования СЭП приведена на рис. 1.11, а. Поясним назначение блоков рассматриваемой структурной схемы. (Начало lw[of%}j / Ввод / исходных 1 данных , Задание начальных услодии 1-7-Ч-Т [=0 3= Расчет входных сигналов -10-- Подпрограм ма униЬерс i&ena 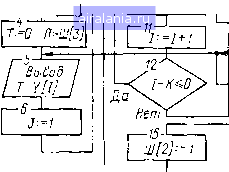 стоп 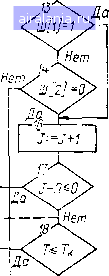 Si Ri Рис. 1.11. Структурные схемы алгоритма цифрового моделирования СЭП и линейного динамического звена Блок 1 предназначен для задания входных воздействий СЭП В [/], шага интегрирования Ш [0], шага печати Ш [3], порядка метода численного интегрирования Ш [/]. Блок 2 обеспечивает ввод параметров всех К звеньев структурной схемы исследуемой АСУ. Блок 3 служит для задания начальных условий координат (переменных) СЭП. Если моделирование производится при нулевых начальных условиях, то этот блок обеспечивает обнуление переменных S и R в начале расчета. Блок 4 предназначен для задания нулевого начального значения теку- ,#1о времени Т и для присвоения целочисленной переменной П значения / [Л], т. е. шага печати. Блок 5 осуществляет вывод текущего времени Т п переменных Y [I] NN печать. Блок 6 устанавливает в состояние «единица» счетчик циклов расчета J, 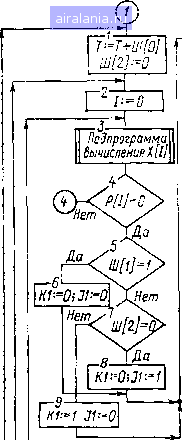 -k2[ljR[JU[])lA0[l] 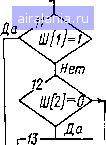 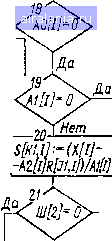 -22. S[K1J]:=S[K1,IJ, RUl}-=R[Kij] + X Ш10]/2
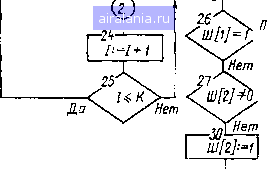
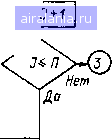 Рис. 1.12. Структурная схема алгоритма моделирования линейного динамического звена Блок 7 определяет текущее время и присваивает переключателю пути иичислеиия Ш [2] нулевое значение. Переключатель Ш [2] используется только при численном методе второго порядка. Г)Лок 8 устанавливает в состояние «нуль» счетчик звена /. 0 1 2 3 4 [5] 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 0.0202 | ||||||||||||||||||